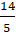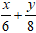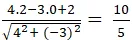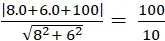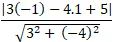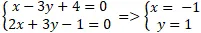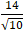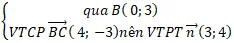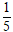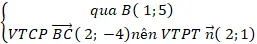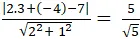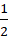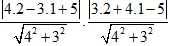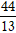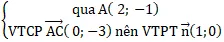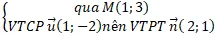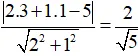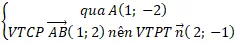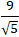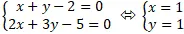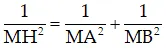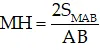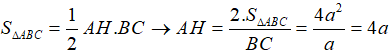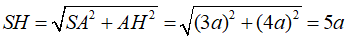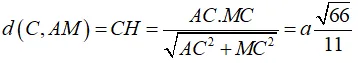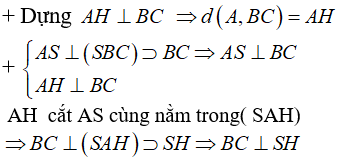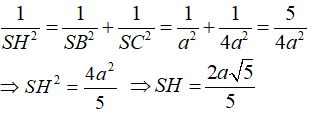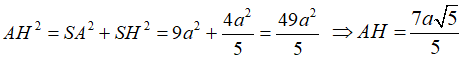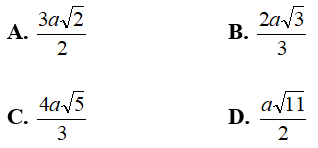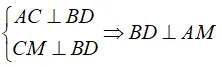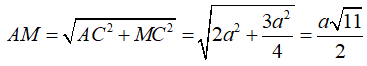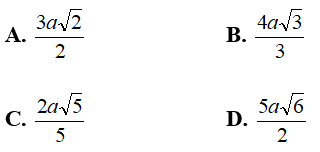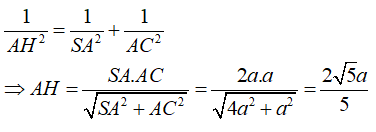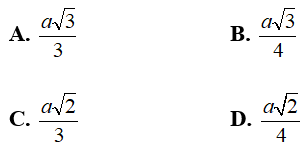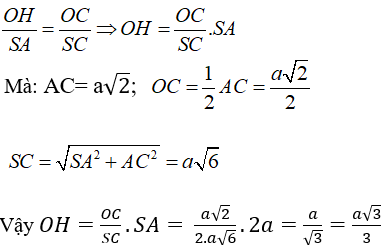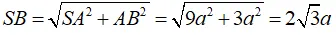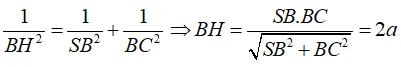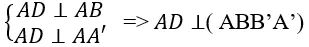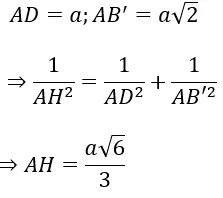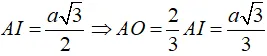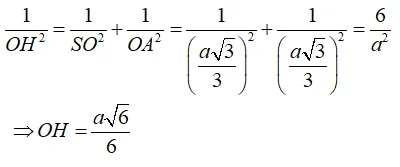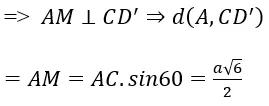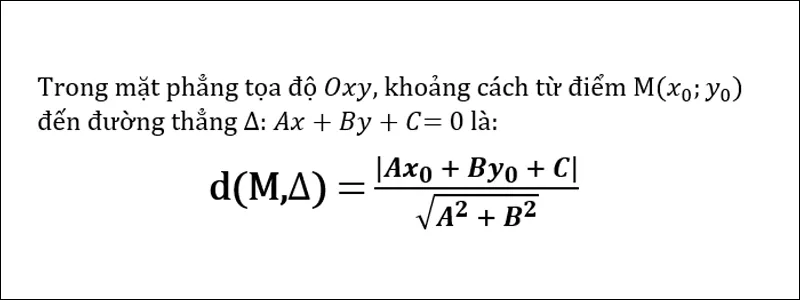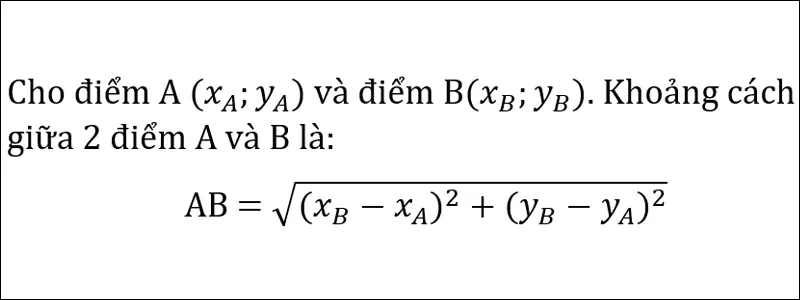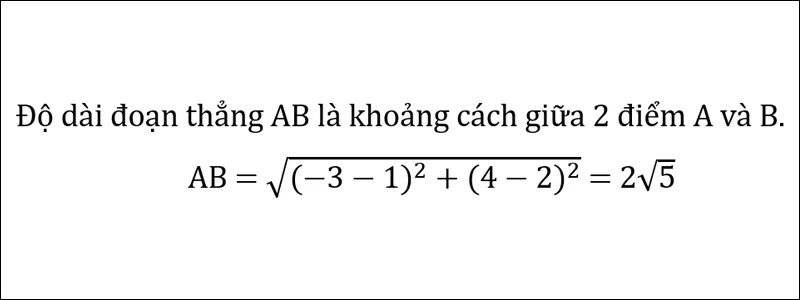Thủ Thuật về Cách xác định khoảng chừng cách từ điểm đến đường thẳng Chi Tiết
Lê Minh Phương đang tìm kiếm từ khóa Cách xác định khoảng chừng cách từ điểm đến đường thẳng được Cập Nhật vào lúc : 2022-02-28 11:52:05 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Tính khoảng chừng cách từ một điểm đến một đường thẳng
Nội dung chính
- Tính khoảng chừng cách từ một điểm đến một đường thẳngCách tính khoảng chừng cách từ một điểm đến một đường thẳng cực hayTrong hình học mặt phẳng Oxy lớp 10 và hình học không khí Oxyz lớp 12 đều có dạng toán tìm khoảng chừng cách từ điểm tới đường thẳng Δ cho trước. Đây là dạng toán tương đối đơn giản, bạn chỉ việc nhớ đúng chuẩn công thức là làm tốt. Nếu bạn quên hoàn toàn có thể xem lại lý thuyết phía dưới, đi kèm với nó là bài tập có lời giải rõ ràng tương ứngKhoảng cách từ 1 điểm đến 1 đường thẳng trong không khí là gì?Khoảng cách từ 1 điểm đến 1 đường thẳng trong không gianĐánh Giá khoảng chừng cách 1 điểm đến đường thẳngVideo hướng dẫn tính khoảng chừng cách từ một điểm đến đường thẳngHướng dẫn công thức khoảng chừng cách từ điểm đến đường thẳng1. Điểm là gì?2. Đường thẳng là gì?3. Khoảng cách từ 1 điểm đến 1 đường thẳng trong không khí là gì?4. Công thức tính khoảng chừng cách từ một điểm đến đường thẳng5. Cách tính khoảng chừng cách từ điểm đến đường thẳng bằng tích có hướng6. Cách tính khoảng chừng cách giữa 2 điểm7. Bài tập tính khoảng chừng cách từ một điểm đến một đường thẳng8. Một số lưu ý về tính khoảng chừng cách từ điểm đến đường thẳngVideo liên quan
Trang trước
Trang sau
Quảng cáo
+ Cho đường thẳng d: ax + by + c = 0 và điểm M ( x0; y0). Khi đó khoảng chừng cách từ điểm
M đến đường thẳng d là: d(M; d) =
+ Cho điểm A( xA; yA) và điểm B( xB; yB) . Khoảng cách hai điểm này là :
AB =
Chú ý: Trong trường hợp đường thẳng d chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng d về dạng tổng quát.
Ví dụ 1: Khoảng cách từ điểm M( 1; -1) đến đường thẳng ( a) : 3x – 4y – 21 = 0 là:
A. 1
B. 2
C. 
Hướng dẫn giải
Khoảng cách từ điểm M đến đường thẳng ( a) là:
d(M;a) =
=
Chọn D.
Ví dụ 2: Khoảng cách từ điểm O đến đường thẳng d:
= 1 là:
A. 4,8
B. 
D. 6
Hướng dẫn giải
Đường thẳng d:
= 1 ⇔ 8x + 6y – 48 = 0
⇒ Khoảng cách từ điểm O đến đường thẳng d là :
d( O; d) =
= 4,8
Chọn A.
Quảng cáo
Ví dụ 3: Khoảng cách từ điểm M(2; 0) đến đường thẳng
là:
A. 2
B. 

Hướng dẫn giải
+ Ta đưa đường thẳng d về dạng tổng quát:
(d) :
⇒ Phương trình ( d) : 4( x – 1) – 3( y – 2) = 0 hay 4x – 3y + 2 = 0
+ Khoảng cách từ điểm M đến d là:
d( M; d) =
= 2
Chọn A.
Ví dụ 4. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng
(d): 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng:
A. R = 4
B. R = 6
C. R = 8
D. R = 10
Lời giải
Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng chừng cách từ tâm đường tròn đến đường thẳng d đó đó là bán kính R của đường tròn
⇒ R= d(O; d) =
= 10
Chọn D.
Ví dụ 5 . Khoảng cách từ điểm M( -1; 1) đến đường thẳng d: 3x – 4y + 5 = 0 bằng:
A. 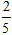
C. 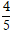
Lời giải
Khoảng cách từ điểm M đến đường thẳng d là:
d( M; d) =
=
Chọn A.
Quảng cáo
Ví dụ 6. Khoảng cách từ giao điểm của hai tuyến đường thẳng (a): x – 3y + 4 = 0 và
(b):
2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:
A. 2√10
B. 

Lời giải
Gọi A là giao điểm của hai tuyến đường thẳng ( a) và ( b) tọa độ điểm A là nghiệm hệ phương trình :
⇒ A( -1; 1)
Khoảng cách từ điểm A đến đường thẳng ∆ là :
d( A; ∆) =
=
Chọn C
Ví dụ 7. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A( 1; 2) ; B(0; 3) và C(4; 0) . Chiều cao của tam giác kẻ từ đỉnh A bằng:
A. 
C. 
Lời giải
+ Phương trình đường thẳng BC:
⇒ ( BC) : 3(x – 0) + 4( y – 3) = 0 hay 3x + 4y – 12 = 0
⇒ chiều cao của tam giác kẻ từ đỉnh A đó đó là khoảng chừng cách từ điểm A đến đường thẳng BC.
d( A; BC) =
=
Chọn A.
Ví dụ 8. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3; -4); B(1; 5) và C(3;1) . Tính diện tích s quy hoạnh tam giác ABC.
A. 10
B. 5
C. √26
D. 2√5
Lời giải
+ Phương trình BC:
⇒Phương trình BC: 2( x – 1) + 1( y – 5) = 0 hay 2x + y – 7 = 0
⇒ d( A;BC) =
= √5
+ BC =
= 2√5
⇒ diện tích s quy hoạnh tam giác ABC là: S =
.d( A; BC).BC =
.√5.2√5 = 5
Chọn B.
Ví dụ 9: Hai cạnh của hình chữ nhật nằm trên hai tuyến đường thẳng d1 : 4x – 3y + 5 = 0 và
d2: 3x + 4y – 5 = 0, đỉnh A( 2; 1). Diện tích của hình chữ nhật là:
A. 1.
B. 2
C. 3
D. 4
Lời giải
+ Nhận xét : điểm A không thuộc hai tuyến đường thẳng trên.
⇒ Độ dài hai cạnh kề của hình chữ nhật bằng khoảng chừng cách từ A(2; 1) đến hai tuyến đường thẳng trên, do đó diện tích s quy hoạnh hình chữ nhật bằng
S =
= 2 .
Chọn B.
Câu 1: Khoảng cách từ điểm M( 2;0) đến đường thẳng
là:
A. 2
B. 

Hiển thị lời giải
Đáp án: A
Trả lời:
+ Ta đưa đường thẳng d về dạng tổng quát:
(d) :
=> Phương trình (d) : 4( x – 1) – 3( y – 2) = 0 hay 4x – 3y + 2 = 0.
+ Khi đó khoảng chừng cách từ M đến d là:
d(M, d)=
= 2
Câu 2: Đường tròn ( C) có tâm I ( -2; -2) và tiếp xúc với đường thẳng
d: 5x + 12y – 10 = 0. Bán kính R của đường tròn ( C) bằng:
A. R = 

D. R =
Hiển thị lời giải
Đáp án: A
Trả lời:
Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng chừng cách từ tâm đường tròn ( C) đến đường thẳng d đó đó là bán kính đường tròn.
=> R = d(I; d) =
=
Câu 3: Hai cạnh của hình chữ nhật nằm trên hai tuyến đường thẳng (a) : 4x – 3y + 5 = 0
và
(b) : 3x + 4y – 5 = 0. Biết hình chữ nhật có đỉnh A( 2 ;1). Diện tích của hình chữ nhật là:
A. 1
B. 2
C. 3
D. 4
Hiển thị lời giải
Đáp án: B
Trả lời:
Ta thấy: điểm A không thuộc hai tuyến đường thẳng trên.
Độ dài hai cạnh kề của hình chữ nhật bằng khoảng chừng cách từ A đến hai tuyến đường thẳng trên.
Độ dài 2 cạnh là: d( A; a) =
= 2; d(A; b) =
= 1
do đó diện tích s quy hoạnh hình chữ nhật bằng : S = 2.1 = 2
Câu 4: Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4) .Tính diện tích s quy hoạnh tam giác ABC ?
A. 3
B. 

Hiển thị lời giải
Đáp án: A
Trả lời:
+ Phương trình đường thẳng AC:
=> Phương trình AC: 1( x – 2) + 0.(y + 1) = 0 hay x – 2= 0..
+ Độ dài AC =
= 3 và khoảng chừng cách từ B đến AC là:
d(B; AC) =
= 2
=> Diện tích tam giác ABC là : S =
AC.d( B;AC) =
.3.2 = 3 .
Câu 5: Khoảng cách từ A(3; 1) đến đường thẳng
gần với số nào sau đây ?
A. 0, 85
B. 0,9
C. 0,95
D. 1
Hiển thị lời giải
Đáp án: B
Trả lời:
Ta đưa đường thẳng d về dạng tổng quát:
(d):
=> ( d): 2(x – 1) + 1( y – 3) = 0 hay 2x + y – 5 = 0
=> d(A, d) =
≈ 0,894
Câu 6: Hai cạnh của hình chữ nhật nằm trên hai tuyến đường thẳng 4x – 3y + 5 = 0 và
3x + 4y + 5 = 0
đỉnh A(2; 1) . Diện tích của hình chữ nhật là
A. 6
B. 2
C. 3
D. 4
Hiển thị lời giải
Đáp án: A
Trả lời:
+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 4x – 3y + 5 = 0 là
= 2
+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 3x + 4y + 5 = 0 là
= 3
=> Diện tích hình chữ nhật bằng 2.3 = 6
Câu 7: Tính diện tích s quy hoạnh hình bình hành ABCD biết A( 1; -2) ; B( 2; 0) và D( -1; 3)
A. 6
B. 4,5
C. 3
D. 9
Hiển thị lời giải
Đáp án: D
Trả lời:
+ Đường thẳng AB:
=> Phương trình AB: 2(x – 1) – 1(y + 2) = 0 hay 2x – y – 4 = 0
+ độ dài đoạn AB: AB =
= √5
Khoảng cách từ D đến AB: d( D; AB)=
=
=> Diện tích hình chữ nhật ABCD là S = AB.d( D; AB) = √5.
= 9
Câu 8: Tính khoảng chừng cách từ giao điểm của hai tuyến đường thẳn (d) : x + y – 2 = 0 và
( ∆) : 2x + 3y – 5 = 0 đến đường thẳng (d’) : 3x – 4y + 11 = 0
A. 1
B. 2
C. 3
D. 4
Hiển thị lời giải
Đáp án: B
Trả lời:
+ Giao điểm A của hai tuyến đường thẳng d và ∆ là nghiệm hệ phương trình
=> A( 1; 1)
+ Khoảng cách từ điểm A đến đường thẳng (d’) là :
d( A; d’) =
= 2
Chuyên đề Toán 10: đầy đủ lý thuyết và những dạng bài tập có đáp án khác:
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Cách tính khoảng chừng cách từ một điểm đến một đường thẳng cực hay
Trang trước
Trang sau
Quảng cáo
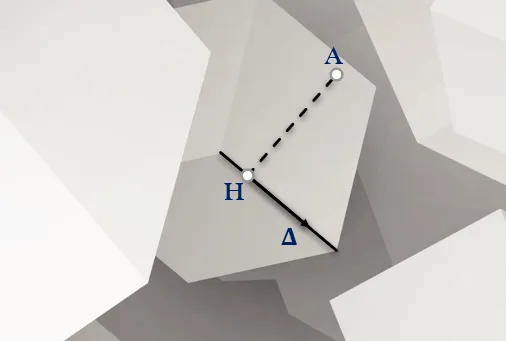
– Để tính khoảng chừng cách từ điểm M đến đường thẳng Δ ta cần xác định được hình chiếu H của điểm M trên đường thẳng Δ. Khi đó MH đó đó là khoảng chừng cách từ M đến đường thẳng. Điểm H thường được dựng theo hai cách sau:
+ Trong mp(M; Δ) vẽ MH vuông góc Δ ⇒ d(M; Δ) = MH
+ Dựng mặt phẳng (α) qua M và vuông góc với Δ tại H ⇒ d(M; Δ) = MH.
– Hai công thức sau thường được dùng để tính MH:
+ Tam giác AMB vuông tại M và có đường cao AH thì
+ MH là đường cao của tam giác MAB thì
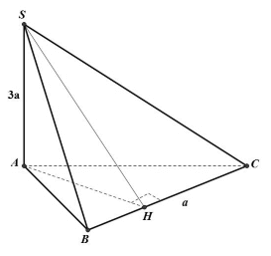
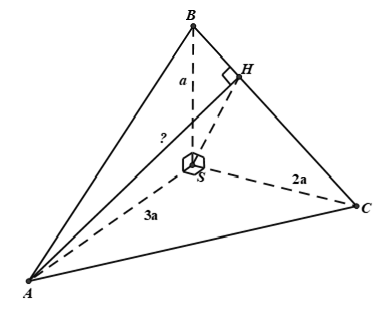
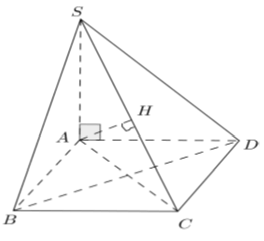
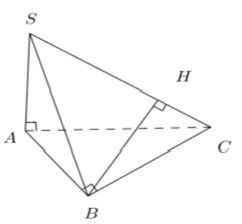
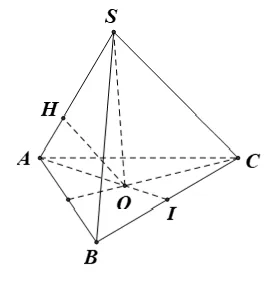
Ví dụ 1: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2; BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?
A. 2aB. 4aC.3aD. 5a
Hướng dẫn giải
+ Kẻ AH vuông góc với BC
Ta có: SA ⊥ (ABC) ⇒ SA ⊥ BC
Lại có: AH ⊥ BC nên BC ⊥ (SAH)
⇒ SH ⊥ BC và khoảng chừng cách từ S đến BC đó đó là SH
+ Ta có tam giác vuông SAH vuông tại A nên ta có
Chọn D
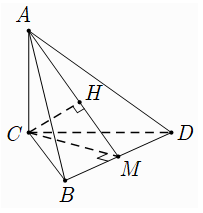
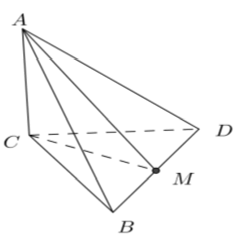
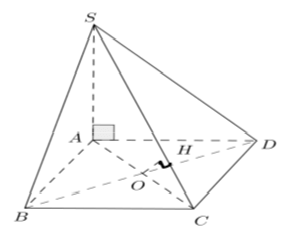
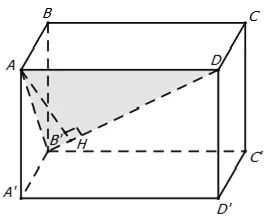
Ví dụ 2: Cho hình chóp ABCD có cạnh AC ⊥ (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC = a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
Quảng cáo
Hướng dẫn giải
+ Do tam giác BCD đều cạnh a nên đường trung tuyến CM đồng thời là đường cao và MC = a√3/2
+ Ta có: AC ⊥ (BCD) ⇒ AC ⊥ CM
Gọi H là chân đường vuông góc kẻ từ C đến AM
Ta có:
Chọn đáp án C
Ví dụ 3: Cho tứ diện SABC trong đó SA; SB; SC vuông góc với nhau từng đôi một và SA = 3a; SB = a; SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:
Hướng dẫn giải
Chọn đáp án B
Xét trong tam giác SBC vuông tại S có SH là đường cao ta có:
+ Ta dễ chứng tỏ được AB ⊥ (SBC) ⊃ SH ⇒ AS ⊥ SH
⇒ tam giác SAH vuông tại S.
Áp dụng định lsi Pytago trong tam giác ASH vuông tại S ta có:
Chọn B
Ví dụ 4: Cho hình chóp A.BCD có cạnh AC ⊥ (BCD) và BCD là tam giác đều cạnh bằng a . Biết AC = a√2 và M là trung điểm của BD . Khoảng cách từ A đến đường thẳng BD bằng:
Hướng dẫn giải
Chọn D
Ta có:
(Định lý 3 đường vuông góc)
⇒ d(A, BD) = AM, CM = a√3/2 (vì tam giác BCD đều).
+ AC vuông góc ( BCD) nên AC vuông góc CM hay tam giác ACM vuông tại C.
⇒
Quảng cáo
Ví dụ 5: Cho hình chóp S.ABCD có SA ⊥ (ABCD) , đáy ABCD là hình thoi cạnh bằng a và ∠B = 60° . Biết SA = 2a. Tính khoảng chừng cách từ A đến SC.
Hướng dẫn giải
Chọn C
Kẻ AH ⊥ SC, khi đó d(A; SC) = AH
+ Do ABCD là hình thoi cạnh bằng a và ∠B = 60° nên tam giác ABC đều ⇒ AC = a
+ Do SA vuông góc (ABCD) nên SA vuông góc AC hay tam giác SAC vuông tại A.
Trong tam giác vuông ta có:
Ví dụ 6: Cho hình chóp S. ABCD có SA ⊥ (ABCD) ; SA = 2a, ABCD là hình vuông vắn cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng chừng cách từ O đến SC.
Hướng dẫn giải
Chọn A
+ Kẻ OH ⊥ SC , khi đó d(O; SC) = OH
+ Ta có: ΔSAC ∼ ΔOHC (g.g) (g-g) nên
Ví dụ 7: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng α. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
Hướng dẫn giải
Chọn D
+ Gọi O là tâm của hình vuông vắn ABCD.
+ Do S.ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD)
+ Theo giả thiết góc giữa cạnh bên và mặt đáy là α nên : ∠SDO = α
Kẻ OH ⊥ SD, khi đó d(O, SD) = OH
Ta có: BD = a√a nên OD = (1/2)BD = (1/2).a√2 = (a√2)/2
+ Xét tam giác vuông OHD:
OH = OD.sinα = (a√2/2).sinα
Câu 1: Cho hình chóp S.ABC trong đó SA; AB; BC vuông góc với nhau từng đôi một. Biết SA = 3a, AB = a√3, BC = a√6. Khoảng cách từ B đến SC bằng
A. a√2 B. 2aC. 2a√3D. a√3
Hiển thị lời giải
Chọn B
+ Vì SA, AB, BC vuông góc với nhau từng đôi một nên CB ⊥ (SAB) ⇒ CB ⊥ SB .
+ Kẻ BH ⊥ SC, khi đó d(B; SC) = BH.
Ta có:
Trong tam giác SBC vuông tại B ta có:
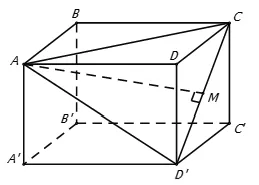
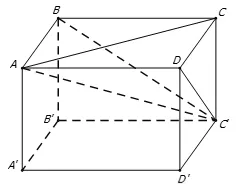
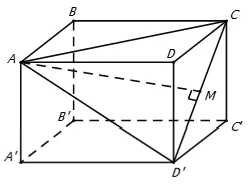
Câu 2: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD’ bằng

Gọi M là trung điểm của CD’
Do ABCD.A’B’C’D’ là hình lập phương nên tam giác ACD’ là tam giác đều cạnh a√2 .
+ Tam giác ACD’ có AM là đường trung tuyến nên đồng thời là đường cao AM ⊥ CD’.
d(A; CD’) = AM = AC.sin(ACM) = a√2.sin60°= (a√6)/2
Đáp án: B
Câu 3: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB’ bằng

Gọi H là chân đường vuông góc hạ từ A xuống DB’.
Ta có:
⇒ AD ⊥ AB’
Xét tam giác ADB’ vuông tại A; đường cao AH:
Đáp án D
Câu 4: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC’ bằng nhau ?
A. A’, B, C’B. B, C, DC. B’, C’, D’D. A, A’, D’
Hiển thị lời giải
Dễ thấy những tam giác ABC’, C’CA, ADC’ là những tam giác vuông bằng nhau nên những đường cao hạ từ đỉnh góc vuông xuống canh huyền cũng bằng nhau.
Vậy: d(B; AC’) = d(C; AC’) = d(D; AC’)
Đáp án B
Câu 5: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SO = a√3/3. Khoảng cách từ điểm O đến cạnh bên SA bằng
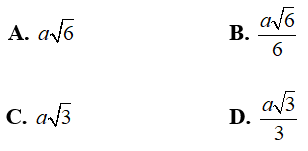
Chọn B
Vì hình chóp S.ABC đều có SO là đường cao
⇒ O là tâm của tam giác ABC.
+ Gọi I là trung điểm cạnh BC.
Tam giác ABC đều nên
Kẻ OH ⊥ SA; khi đó d(O; SA) = OH
Xét tam giác SAO vuông tại O:
Câu 6: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD’ bằng
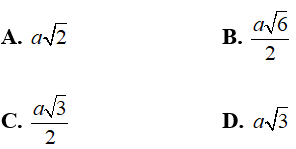
Gọi M là trung điểm của CD’
Do ABCD.A’B’C’D’ là hình lập phương nên tam giác ACD’ là tam giác đều cạnh a√2
Đáp án: B
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Trong hình học mặt phẳng Oxy lớp 10 và hình học không khí Oxyz lớp 12 đều có dạng toán tìm khoảng chừng cách từ điểm tới đường thẳng Δ cho trước. Đây là dạng toán tương đối đơn giản, bạn chỉ việc nhớ đúng chuẩn công thức là làm tốt. Nếu bạn quên hoàn toàn có thể xem lại lý thuyết phía dưới, đi kèm với nó là bài tập có lời giải rõ ràng tương ứng
Khoảng cách từ 1 điểm đến 1 đường thẳng trong không khí là gì?
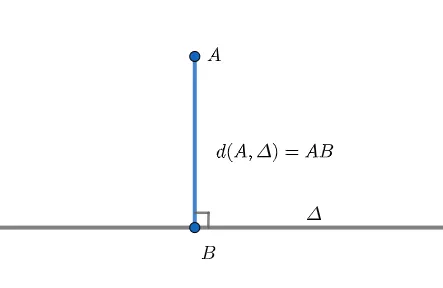
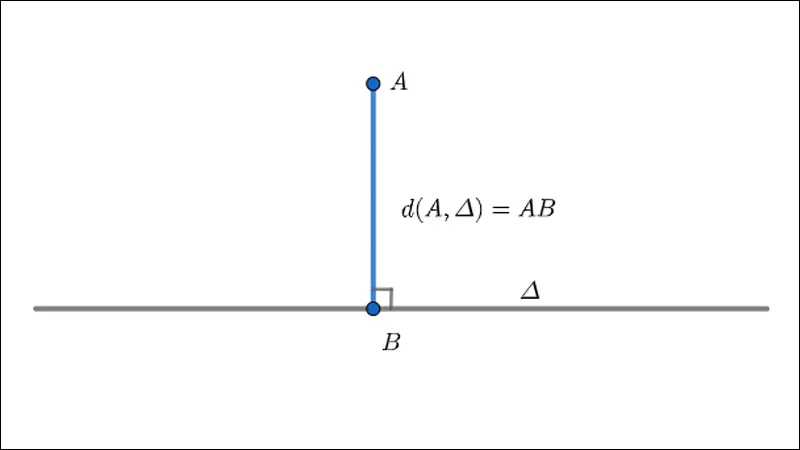
Trong không khí cho điểm A và đường thẳng Δ bất kỳ. Gọi điểm B là hình chiếu của điểm A lên đường thẳng Δ. Khi đó độ dài đoạn thẳng AB đó đó là khoảng chừng cách từ điểm A lên đường thẳng Δ.
Hay nói cách khác khoảng chừng cách giữa điểm và đường thẳng đó đó là khoảng chừng cách giữa điểm và hình chiếu của nó trên đường thẳng. Ký hiệu là d(A,Δ).
Tham khảo thêm:
Khoảng cách từ 1 điểm đến 1 đường thẳng trong không khí
Khoảng cách từ 1 điểm đến 1 đường thẳng trong không khí được tính ra làm sao? Bài viết dưới đây hướng dẫn những em 2 phương pháp để tính khoảng chừng cách từ 1 điểm đến đường thẳng. Các em cùng theo dõi nhé!
Nội Dung
- 1 KHOẢNG CÁCH TỪ ĐIỂM ĐẾN 1 ĐƯỜNG THẲNG TRONG KHÔNG GIAN2 CÔNG THỨC TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN 1 ĐƯỜNG THẲNG TRONG KHÔNG GIAN OXYZ
- 2.1 1. TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN 1 ĐƯỜNG THẲNG TRONG OXYZ BẰNG CÁCH TÌM HÌNH CHIẾU2.2 2. TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN ĐƯỜNG THẲNG TRONG OXYZ BẰNG TÍCH CÓ HƯỚNG
Đánh Giá khoảng chừng cách 1 điểm đến đường thẳng
Đánh Giá – 9.3
Đánh Giá – 9.7
9.5
100
Hướng dẫn khoảng chừng cách từ 1 điểm đến 1 đường thẳng oke ạ !
User Rating: 4.65 ( 1 votes)
Trong hình học không khí Oxyz thường có dạng toán tìm khoảng chừng cách từ điểm đến đường thẳng cho trước. Đây là một dạng toán khá đơn giản và phổ biến mà chỉ việc nhớ đúng chuẩn công thức và áp dụng vào giải toán thuận tiện và đơn giản. Hãy theo dõi nội dung bài viết này để tìm hiểu công thức tính khoảng chừng cách từ 1 điểm đến đường thẳng nhé! Hãy tìm hiểu dưới đây với Mobitool nhé !
Video hướng dẫn tính khoảng chừng cách từ một điểm đến đường thẳng
Hướng dẫn công thức khoảng chừng cách từ điểm đến đường thẳng
Hãy tham khảo công thức khoảng chừng cách từ điểm đến đường thẳng tiên tiến nhất dưới đây :
1. Điểm là gì?
Điểm trong khái niệm toán học đơn giản được thừa nhận như một khái niệm xuất phát để xây dựng môn hình học, được tưởng tượng là một thứ rất nhỏ bé, không còn kích thước hay kích thước bằng không.
2. Đường thẳng là gì?
Đường thẳng là một đường dài vô hạn, mỏng dính vô cùng và thẳng tuyệt đối.
3. Khoảng cách từ 1 điểm đến 1 đường thẳng trong không khí là gì?
Trong không khí cho điểm A và đường thẳng Δ bất kỳ. Gọi điểm B là hình chiếu của điểm A lên đường thẳng Δ. Khi đó độ dài đoạn thẳng AB đó đó là khoảng chừng cách từ điểm A lên đường thẳng Δ.
Khoảng cách từ điểm đến đường thẳng trong không khí
Nói cách khác, khoảng chừng cách từ điểm đến đường thẳng trong không khí là khoảng chừng cách giữa điểm và hình chiếu của nó trên đường thẳng. Ký hiệu là d(A,Δ).
4. Công thức tính khoảng chừng cách từ một điểm đến đường thẳng
Công thức tính khoảng chừng cách từ điểm đến đường thẳng
5. Cách tính khoảng chừng cách từ điểm đến đường thẳng bằng tích được bố trí theo hướng
Cách tính khoảng chừng cách từ điểm đến đường thẳng bằng tích được bố trí theo hướng
Ví dụ:
Ví dụ về tính khoảng chừng cách từ điểm đến đường thẳng bằng tích được bố trí theo hướng
Lời giải:
Lời giải của ví dụ trên
6. Cách tính khoảng chừng cách giữa 2 điểm
Cách tính khoảng chừng cách giữa 2 điểm
Ví dụ: Trong mặt phẳng Oxy, cho điểm A (1;2) và điểm B(-3;4). Tính độ dài đoạn thẳng AB.
Lời giải:
Lời giải của ví dụ trên
7. Bài tập tính khoảng chừng cách từ một điểm đến một đường thẳng
Bài 1: Cho một đường thẳng có phương trình có dạng Δ: – x + 3y + 1 = 0. Hãy tính khoảng chừng cách từ điểm Q. (2;1) tới đường thẳng Δ.
Lời giải:
Lời giải của bài tập 1
Bài 2:
Bài tập 2
Lời giải:
Lời giải của bài tập 2
Bài 3:
Bài tập 3
Lời giải:
Lời giải của bài tập 3
Bài 4: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Tính bán kính R của đường tròn (C).
Lời giải:
Lời giải của bài tập 4
Bài 5: Tính Khoảng cách từ giao điểm của hai tuyến đường thẳng (a): x – 3y + 4 = 0 và (b): 2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0.
Lời giải:
Lời giải của bài tập 5
Bài 6: Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4) .Tính diện tích s quy hoạnh tam giác ABC?
Lời giải:
Lời giải của bài tập 6
Bài 7:
Bài tập 7
Lời giải:
Lời giải của bài tập 7
8. Một số lưu ý về tính khoảng chừng cách từ điểm đến đường thẳng
– Cần xác định được khái niệm khoảng chừng cách từ điểm đến đường thẳng là ra làm sao.
– Đưa phương trình đường thẳng về dạng tổng quát trước khi áp dụng công thức tính khoảng chừng cách từ điểm đến đường thẳng .
– Nên sử dụng máy tính cầm tay để hoàn toàn có thể tương hỗ tính khoảng chừng cách từ điểm đến đường thẳng một cách nhanh gọn và đúng chuẩn nhất.
Sử dụng máy tính cầm tay để tính khoảng chừng cách từ điểm đến đường thẳng nhanh gọn
Xem thêm : Hướng dẫn lim căn bậc n của n
Từ khóa tìm kiếm : khoảng chừng cách từ điểm tới đường thẳng, công thức tính khoảng chừng cách từ một điểm đến đường thẳng, công thức tính khoảng chừng cách điểm đến đường thẳng, công thức tính khoảng chừng cách từ 1 điểm đến 1 đường thẳng, công thức tính khoảng chừng cách từ một điểm đến một đường thẳng, khoảng chừng cách từ điểm đến đường thẳng oxyz, công thức tính khoảng chừng cách giữa điểm và đường thẳng, tìm khoảng chừng cách từ điểm đến đường thẳng, cách xác định khoảng chừng cách từ 1 điểm đến đường thẳng, công thức khoảng chừng cách từ 1 điểm đến 1 đường thẳng, phương pháp tính khoảng chừng cách từ 1 điểm đến 1 đường thẳng, tính khoảng chừng cách từ một điểm đến đường thẳng, tính khoảng chừng cách điểm đến đường thẳng, tìm khoảng chừng cách từ 1 điểm đến đường thẳng, khoảng chừng cách từ 1 điểm đến 1 đường thẳng là gì, khoảng chừng cách một điểm đến đường thẳng, khoảng chừng cách 1 điểm đến 1 đường thẳng, khoảng chừng cách từ một điểm đến một đường thẳng trong không khí, công thức khoảng chừng cách, khoảng chừng cách 1 điểm đến đường thẳng oxyz, khoảng chừng cách điểm đến đường thẳng oxyz, phương pháp tính khoảng chừng cách từ một điểm đến một đường thẳng, công thức tính khoảng chừng cách 1 điểm đến đường thẳng, tính khoảng chừng cách giữa điểm và đường thẳng, ct tính khoảng chừng cách từ điểm đến đường thẳng, khoảng chừng cách từ 1 điểm đến 1 đường thẳng trong oxyz, khoảng chừng cách từ tâm đến đường thẳng, khoảng chừng cách giữa 1 điểm và 1 đường thẳng, tính khoảng chừng cách 1 điểm đến đường thẳng, khoảng chừng cách từ 1 điểm đến đường thẳng trong oxyz, khoang cach tu diem den duong thang, khoảng chừng cách giữa 1 điểm và đường thẳng, khoảng chừng cách từ điểm đến đoạn thẳng, công thức khoảng chừng cách điểm đến đường thẳng, công thức từ điểm đến đường thẳng, khoảng chừng cách từ 1 điểm đến 1 đường thẳng trong oxy, gọi khoảng chừng cách từ điểm i đến đường thẳng a là d, khoảng chừng cahcs từ điểm đến đường thẳng, công thức tính độ dài từ điểm đến đường thẳng, công thức tính khoảng chừng cách từ tâm đến đường thẳng, khoảng chừng cách từ 1 điểm tới 1 đường thẳng, công thức tính khoảng chừng cách từ điểm đến đường thẳng trong không khí, khoảng chừng cách từ điểm tới đường, phương pháp tính khoảng chừng cách từ một điểm đến đường thẳng, khoảng chừng cách điểm tới đường thẳng, khoảng chừng cách ký hiệu là gì, khoảng chừng cách từ 1 điểm đến dường thẳng, kc từ điểm đến đt, khoảng chừng cách từ một điểm tới một đường thẳng, công thức từ 1 điểm đến đường thẳng, khoảng chừng cách từ điểm đến đường thẳng trong hệ oxyz, công thức tính khoảng chừng cách từ 1 điểm đến đt, tính độ dài từ 1 điểm đến đường thẳng, khoảng chừng cách từ 1 điểm đến 1 đoạn thẳng, công thức tính khoảng chừng cách từ điểm tới đường thẳng, khoảng chừng cách từ điểm đến một đường thẳng, tính khoảng chừng cách từ điểm tới đường thẳng, khoang cach tu 1 diem den 1 duong thang, độ dài từ 1 điểm đến 1 đường thẳng, khoảng chừng cách từ một điểm đến một đường thẳng là gì, tính khoảng chừng cách giữa 1 điểm đến đường thẳng, phương trình khoảng chừng cách, công thức tính khoảng chừng cách d, khoảng chừng cách từ từ, khoảng chừng cách từ một điểm đến một đoạn thẳng, khoảng chừng cách từ điểm đến đường thẳng oxy, khoảng chừng cách từ một điểm đến 1 đường thẳng, tính khoảng chừng cách d, tính khoảng chừng cách từ điểm đến đoạn thẳng, công thức tiính khoảng chừng cách, khoảng chừng cách điểm và đường thẳng, công thức tính khoảng chừng cách r, khoảng chừng cách từ 1 điểm đến 1 vecto, tính khoảng chừng cách trong không khí oxyz,
phương pháp tính khoảng chừng cách từ 1 điểm đến 1 đường thẳng cách xác định khoảng chừng cách từ 1 điểm đến đường thẳng công thức khoảng chừng cách từ 1 điểm đến 1 đường thẳng công thức tính khoảng chừng cách điểm đến đường thẳng công thức tính khoảng chừng cách giữa điểm và đường thẳng công thức tính khoảng chừng cách từ 1 điểm đến 1 đường thẳng công thức tính khoảng chừng cách từ một điểm đến đường thẳng công thức tính khoảng chừng cách từ một điểm đến một đường thẳng Đời sống Hỏi đáp khoảng chừng cách từ điểm đến đường thẳng oxyz khoảng chừng cách từ điểm tới đường thẳng tìm khoảng chừng cách từ điểm đến đường thẳng Wiki – Thuật ngữ

Video Cách xác định khoảng chừng cách từ điểm đến đường thẳng ?
Bạn vừa tham khảo tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video Cách xác định khoảng chừng cách từ điểm đến đường thẳng tiên tiến nhất
Chia Sẻ Link Download Cách xác định khoảng chừng cách từ điểm đến đường thẳng miễn phí
Heros đang tìm một số trong những ShareLink Tải Cách xác định khoảng chừng cách từ điểm đến đường thẳng Free.
Thảo Luận thắc mắc về Cách xác định khoảng chừng cách từ điểm đến đường thẳng
Nếu sau khi đọc nội dung bài viết Cách xác định khoảng chừng cách từ điểm đến đường thẳng vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Cách #xác #định #khoảng chừng #cách #từ #điểm #đến #đường #thẳng – 2022-02-28 11:52:05