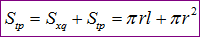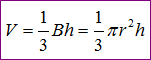Thủ Thuật Hướng dẫn Hình nón tròn xoay là gì Mới Nhất
Bùi Đức Thìn đang tìm kiếm từ khóa Hình nón tròn xoay là gì được Cập Nhật vào lúc : 2022-03-26 20:47:08 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Thể tích khối nón tính ra làm sao? Bài viết dưới đây tôi sẽ tổng hợp tất cả những công thức liên quan đến khối nón để những bạn tiện tra cứu.
Nội dung chính- I. HÌNH NÓN TRÒN XOAY – KHỐI NÓN TRÒN XOAY1. MẶT NÓN TRÒN XOAY2. HÌNH NÓN VÀ KHỐI NÓNII. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, THỂ TÍCH KHỐI NÓN1. DIỆN TÍCH XUNG QUANH CỦA HÌNH NÓN2. DIỆN TÍCH TOÀN PHẦN HÌNH NÓN3. THỂ TÍCH KHỐI NÓN TRÒN XOAY4. THỂ TÍCH KHỐI NÓN TRONG ĐỀ THI THPT QGVideo liên quan
I. HÌNH NÓN TRÒN XOAY – KHỐI NÓN TRÒN XOAY
Trước tiên tất cả chúng ta hãy cũng tìm hiểu và phân biệt những khái niệm mặt nón, hình nón và khối nón.
1. MẶT NÓN TRÒN XOAY
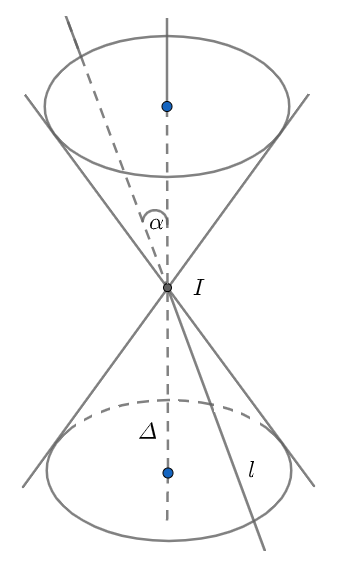
Cho hai tuyến đường thẳng l và Δ cắt nhau tại điểm I và tạo với nhau góc α. Cho mặt phẳng chứa l và Δ quay quanh trục Δ thì đường thẳng l sẽ tạo nên 1 mặt tròn xoay gọi là mặt nón.
Đường thẳng Δ gọi là trục, đường thẳng l gọi là đường sinh, 2α được gọi là góc ở đỉnh, điểm I được gọi là đỉnh của mặt nón. Như vậy khi nói mặt nón ta thấy nó không còn số lượng giới hạn về thể tích và diện tích s quy hoạnh.
2. HÌNH NÓN VÀ KHỐI NÓN
Trước hết ta hoàn toàn có thể hiểu rằng hình nón là một phần của mặt nón và có thêm mặt đáy. Cụ thể, hình nón hoàn toàn có thể được xây dựng như sau:
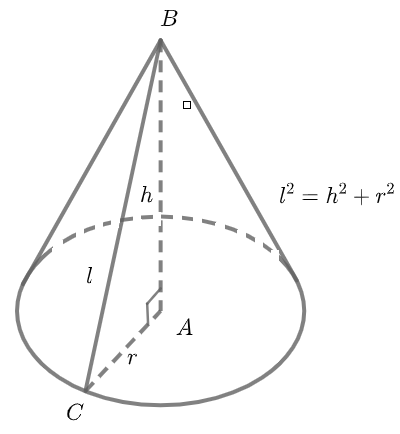
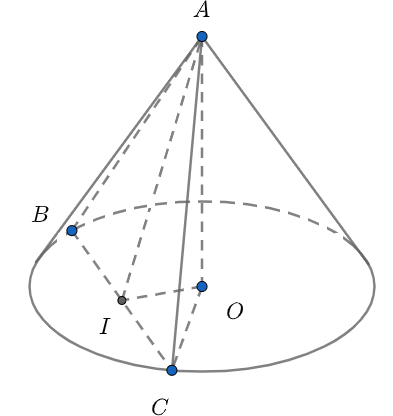
Cho tam giác ABC vuông tại A, quay đoạn gấp khúc BCA quanh trục AB sẽ tạo nên hình nón. Đoạn CA sẽ tạo nên mặt đáy là một hình tròn trụ bán kinh r=CA. Đoạn BC sẽ tạo nên mặt xung quanh. Hình nón tạo thành có độ dài đường sinh là l=BC và độ cao của hình nón là h=AB. Điểm B gọi là đỉnh hình nón. Góc ở đỉnh của hình nón là 2 lần góc ABC.
Còn khối nón đơn giản là hình nón thêm vào đó phần bên trong của hình nón. Chỉ rất khác nhau là khốι nón thì hoàn toàn có thể tích, còn hình nón thì không còn. :))
II. DIỆN TÍCH XUNG QUANH, DIỆN TÍCH TOÀN PHẦN, THỂ TÍCH KHỐI NÓN
1. DIỆN TÍCH XUNG QUANH CỦA HÌNH NÓN
Khi cắt mặt xung quanh của hình nón theo một đường sinh ta được một hình quạt có tâm là đỉnh hình nón, có bán kính bằng độ dài đường sinh, có độ dài cung chính bằng chu vi đáy hình nón. Vì vậy công thức tính diện tích s quy hoạnh xung quanh hình nón là
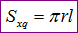
Trong công thức diện tích s quy hoạnh xung quanh hình nón ở trên thì r là bán kính đáy hình nón và l là độ dài đường sinh.
2. DIỆN TÍCH TOÀN PHẦN HÌNH NÓN
Diện tích toàn phần của hình nón bằng diện tích s quy hoạnh xung quanh công với diện tích s quy hoạnh đáy.
Trong số đó r là bán kính đáy hình nón và l là độ dài đường sinh.
3. THỂ TÍCH KHỐI NÓN TRÒN XOAY
Ta hoàn toàn có thể thấy công thức thể tích nón tương tự như công thức tính thể tích khô’i chóp.
Trong công thức trên B là diện tích s quy hoạnh đáy hình nón, r là bán kính đáy hình nón, h là độ cao hình nón.
4. THỂ TÍCH KHỐI NÓN TRONG ĐỀ THI THPT QG
Như vậy tôi đã ra mắt tới những bạn những công thức liên quan đến hình chóp, khối chóp. Hãy rèn luyện và vận dụng thật tốt nhé. Chúc những bạn thành công!
 Tải app VietJack. Xem lời giải nhanh hơn!
Tải app VietJack. Xem lời giải nhanh hơn! Quảng cáo
I. MẶT NÓN
1. Mặt nón tròn xoay
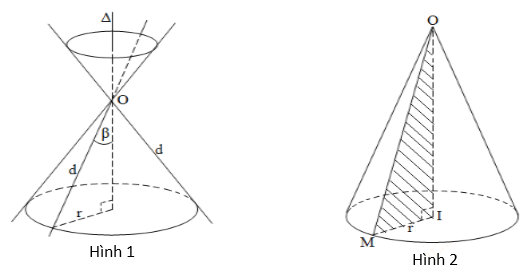
Trong mặt phẳng (P), cho 2 đường thẳng d, Δ cắt nhau tại O và chúng tạo thành góc β với 0o < β ≤ 90o . Khi quay mp(P) xung quanh trục Δ với góc β không thay đổi được gọi là mặt nón tròn xoay đỉnh O (hình 1).
- Người ta thường gọi tắt mặt nón tròn xoay là mặt nón.
- Đường thẳng Δ gọi là trục, đường thẳng d được gọi là đường sinh và góc 2β gọi là góc ở đỉnh.
2. Hình nón tròn xoay
Cho ΔOIM vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).
- Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.
- Hình tròn tâm I, bán kính r = IM là đáy của hình nón.
3. Công thức diện tích hình nón và thể tích khối nón
Cho hình nón có chiều cao là h, bán kính đáy r và đường sinh là l thì có:
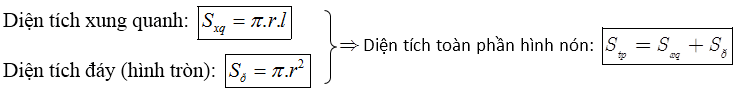
- Thể tích khối nón: 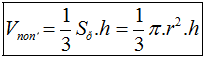
4. Tính chất:
- TH1: Nếu cắt mặt nón tròn xoay bởi mp(P) đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mp(P) cắt mặt nón theo 2 đường sinh ⇒ Thiết diện là tam giác cân.
+ Nếu mp(P) tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.
- TH2: Nếu cắt mặt nón tròn xoay bởi mp(Q.) không đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mp(Q.) vuông góc với trục hình nón ⇒ giao tuyến là một đường tròn.
+ Nếu mp(Q.) song song với 2 đường sinh hình nón giao tuyến là 2 nhánh của 1 hypebol.
+ Nếu mp(Q.) song song với 1 đường sinh hình nón giao tuyến là 1 đường parabol.
Quảng cáo
II. MẶT TRỤ
1. Mặt trụ tròn xoay
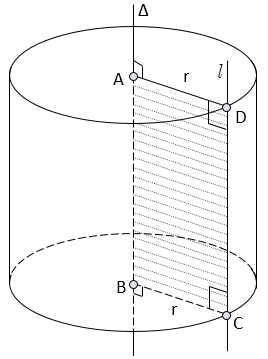
Trong mp(P) cho hai đường thẳng Δ và l song song nhau, cách nhau một khoảng r. Khi quay mp(P) quanh trục cố định Δ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ.
- Đường thẳng Δ được gọi là trục.
- Đường thẳng l được gọi là đường sinh.
- Khoảng cách r được gọi là bán kính của mặt trụ.
2. Hình trụ tròn xoay
Khi quay hình chữ nhật ABCD xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh AB thì đường gấp khúc ABCD tạo thành một hình, hình đó được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ.
- Đường thẳng AB được gọi là trục.
- Đoạn thẳng CD được gọi là đường sinh.
- Độ dài đoạn thẳng AB = CD = h được gọi là chiều cao của hình trụ.
- Hình tròn tâm A, bán kính r = AD và hình tròn tâm B, bán kính r = BC được gọi là 2 đáy của hình trụ.
- Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không khí giới hạn bởi hình trụ tròn xoay kể cả hình trụ.
3. Công thức tính diện tích hình trụ và thể tích khối trụ
Cho hình trụ có chiều cao là và bán kính đáy bằng r, khi đó:
- Diện tích xung quanh của hình trụ: Sxq = 2πrh
- Diện tích toàn phần của hình trụ: Stp = Sxq + 2.SĐay = 2πrh + 2πr2
- Thể tích khối trụ: V = B.h = πr2h
Quảng cáo
4. Tính chất:
- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mp(α) vuông góc với trục Δ thì ta được đường tròn có tâm trên α và có bán kính bằng r với r cũng chính là bán kính của mặt trụ đó.
- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mp(α) không vuông góc với trục Δ nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2r và trục lớn bằng 2r/sinφ, trong đó φ là góc giữa trục Δ và mp(α) với 00 < φ < 900.
- Cho mp(α) song song với trục Δ của mặt trụ tròn xoay và cách Δ một khoảng d.
+ Nếu d < r thì mp(α) cắt mặt trụ theo hai đường sinh ⇒ thiết diện là hình chữ nhật.
+ Nếu d = r thì mp(α) tiếp xúc với mặt trụ theo một đường sinh.
+ Nếu d > r thì mp(α) không cắt mặt trụ.
Lý thuyết và bài tập trắc nghiệm có đáp án và lời giải rõ ràng Toán lớp 12 khác:
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
mat-non-mat-tru-mat-cau.jsp
[embed]https://www.youtube.com/watch?v=90MJIjQ96kk[/embed]