Thủ Thuật về Cho hình chóp sabc có đáy abc là tam giác vuông cân tại b, cạnh bên sa vuông góc với đáy 2022
Bùi Minh Chính đang tìm kiếm từ khóa Cho hình chóp sabc có đáy abc là tam giác vuông cân tại b, cạnh bên sa vuông góc với đáy được Update vào lúc : 2022-03-26 17:47:10 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.
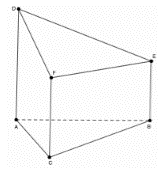
- CÂU HỎI HOT CÙNG CHỦ ĐỀCho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA = a và vuông góc với đáy. Mặt phẳng qua A vuông góc với SC cắt hình chóp theo một thiết diện. Tính diện tích s quy hoạnh thiết diện đó.CÂU HỎI HOT CÙNG CHỦ ĐỀVideo liên quan
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A, AB=a,AC=a3. Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
Xem đáp án » 02/08/2022 2,526
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy. Biết SA=BC=a, thể tích khối chóp S.ABC bằng:
Xem đáp án » 31/07/2022 2,271
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SC = 3a và SC vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng:
Xem đáp án » 31/07/2022 1,743
Đáy của hình chóp S.ABCD là một hình vuông vắn cạnh a. Cạnh bên SA vuông góc với mặt đáy và có dộ dài là a. Thể tích khối tứ diện S.BCD bằng:
Xem đáp án » 31/07/2022 620
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng BD'=a6. Thể tích của khối lăng trụ?
Xem đáp án » 02/08/2022 486
Cho hình lập phương ABCD.A'B'C'D' có diện tích s quy hoạnh mặt chéo ACC’A’ bằng 22 a2. Thể tích của khối lập phương ABCD.A’B’C’D’ bằng:
Xem đáp án » 31/07/2022 323
Cho khối chóp S.ABCD hoàn toàn có thể tích bằng 4a3, đáy ABCD là hình bình hành. Gọi M là trung điểm cạnh SD. Biết diện tích s quy hoạnh tam giác SAB bằng a2. Tính khoảng chừng cách từ M tới mặt phẳng (SAB)
Xem đáp án » 31/07/2022 196
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. AD⊥ABC,AD+BE+CF=5, diện tích s quy hoạnh ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:
Xem đáp án » 02/08/2022 176
Cho khối chóp S.ABC có những góc phẳng ở đỉnh S bằng 60°, SA=1,SB=2,SC=3. Thể tích của khối chóp S.ABC bằng:
Xem đáp án » 02/08/2022 174
Lăng trụ đứng tứ giác có đáy là hình thoi mà những đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần độ cao lăng trụ. Tính thể tích khối lăng trụ
Xem đáp án » 02/08/2022 174
Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45°. Thể tích khối chóp S.ABCD là:
Xem đáp án » 31/07/2022 168
Mệnh đề nào dưới đây sai?
Xem đáp án » 31/07/2022 68
Cho tứ diện ABCD hoàn toàn có thể tích bằng 18. Gọi A1 là trọng tâm của tam giác BCD; (P) là mặt phẳng qua A sao cho góc giữa (P) và mặt phẳng (BCD) bằng 60°. Các đường thẳng qua B, C, D song song với AA1 cắt (P) lần lượt tại B1,C1,D1. Thể tích khối tứ diện A1B1C1D1 bằng?
Xem đáp án » 02/08/2022 68
Cho hình chóp S.ABC có SA⊥SB,SB⊥SC,SA⊥SC; SA=2a,SB=b,SC=c. Thể tích khối chóp là:
Xem đáp án » 31/07/2022 67
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên SA = a và vuông góc với đáy. Mặt phẳng qua A vuông góc với SC cắt hình chóp theo một thiết diện. Tính diện tích s quy hoạnh thiết diện đó.
Câu 33753 Vận dụng cao
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$, $AB = a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Mặt phẳng qua $A$ vuông góc với $SC$ cắt hình chóp theo một thiết diện. Tính diện tích s quy hoạnh thiết diện đó.
Đáp án đúng: d
Phương pháp giải
Giả sử mặt phẳng qua $A$ vuông góc với $SC$ cắt hình chóp theo một thiết diện là tam giác $ADE.$
$beginarrayldfracV_S.ADEV_S.ACB = dfracSDSC.dfracSESB Rightarrow V_S.ADE\V_S.ADE = dfrac13SD.S_ADE Rightarrow S_ADEendarray$
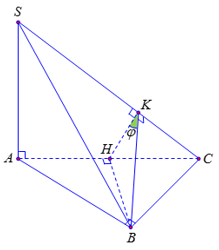
...Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng?
Đáp án A
Gọi H là trung điểm cạnh AC
Ta có (SAC)⊥(ABC) (vì SA⊥(ABC)) và BH⊥AC ⇒ BH⊥(SAC)
Trong mặt phẳng (SAC), kẻ HK⊥SC thì SC⊥(BHK) ⇒ SC⊥BK
⇒ (SAC);(SBC^)=(SKH^)=φ
Mặt khác
Tam giác ABC vuông cân tại B có AB = BC = a nên AC = a2 và BH = a22
Hai tam giác CKH và CAS đồng dạng nên HK = HC.SASC ⇔HC.SASA2+AC2=a23
Tam giác BHK vuông tại H có tanφ = BHBK=3⇒φ=600
Vậy (SAC);(SBC^)=600
CÂU HỎI HOT CÙNG CHỦ ĐỀ
[embed]https://www.youtube.com/watch?v=FMO8aZqB5K4[/embed]