Thủ Thuật về Đường thẳng d song song với mp P thì giữa chúng có bao nhiêu điểm chung 2022
Hà Trần Thảo Minh đang tìm kiếm từ khóa Đường thẳng d song song với mp P thì giữa chúng có bao nhiêu điểm chung được Cập Nhật vào lúc : 2022-03-29 16:40:14 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Thành thạo cách chứng tỏ đường thẳng song song với mặt phẳng sẽ giúp những em học viên hoàn toàn có thể chứng tỏ được hai mặt phẳng song song với nhau.
Nội dung chính- 1. Vị trí tương đối của đường thẳng và mặt phẳngĐịnh nghĩa đường thẳng và mặt phẳng song song.Tính chất của đường thẳng và mặt phẳng song song.2. Phương pháp chứng tỏ đường thẳng song song với mặt phẳng3. Ví dụ cách đường thẳng song song với mặt phẳng4. Bài tập chứng tỏ đường thẳng song song với mặt phẳngVideo liên quan
Xem thêm 3 cách chứng tỏ hai mặt phẳng song song
1. Vị trí tương đối của đường thẳng và mặt phẳng
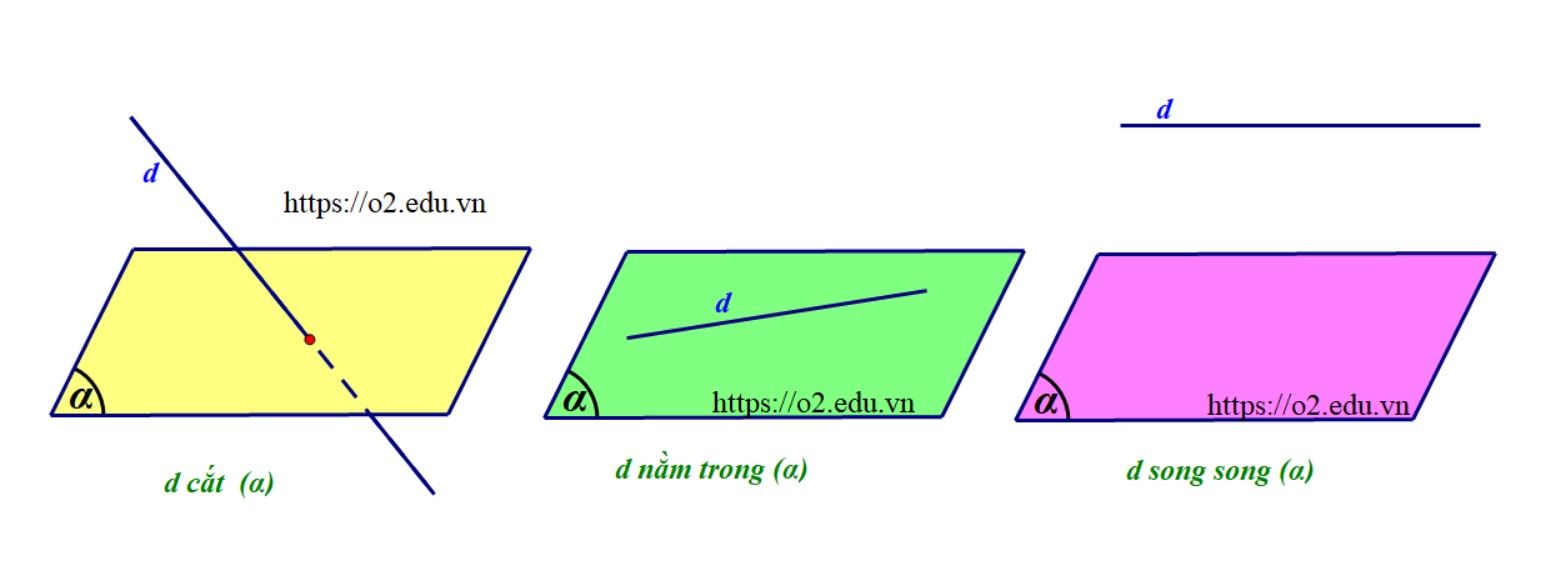
Trong không khí, xét một đường thẳng $d$ và mặt phẳng $(alpha)$ thì có ba kĩ năng về vị trí giữa chúng:
- Đường thẳng $d$ cắt $ (alpha) $: có một điểm chung.
Đường thẳng $d$ nằm trên $ (alpha) $: có vô số điểm chung.
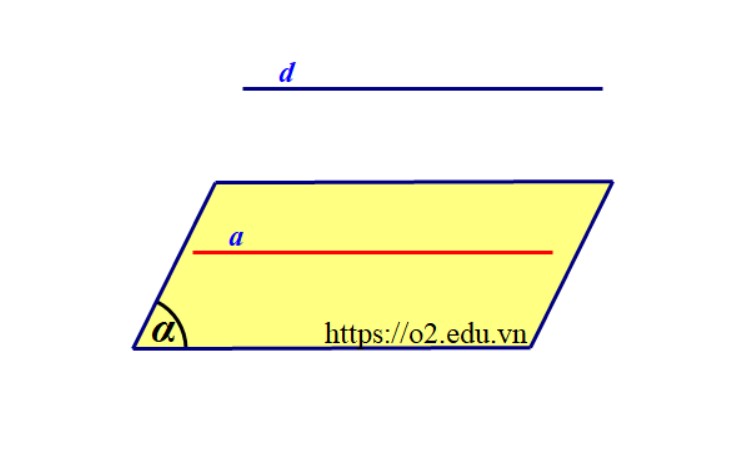
Đường thẳng $ d $ song song $ (alpha) $: không còn điểm chung.
Định nghĩa đường thẳng và mặt phẳng song song.
Đường thẳng và mặt phẳng được gọi là song song nếu chúng không còn điểm chung.
Tính chất của đường thẳng và mặt phẳng song song.
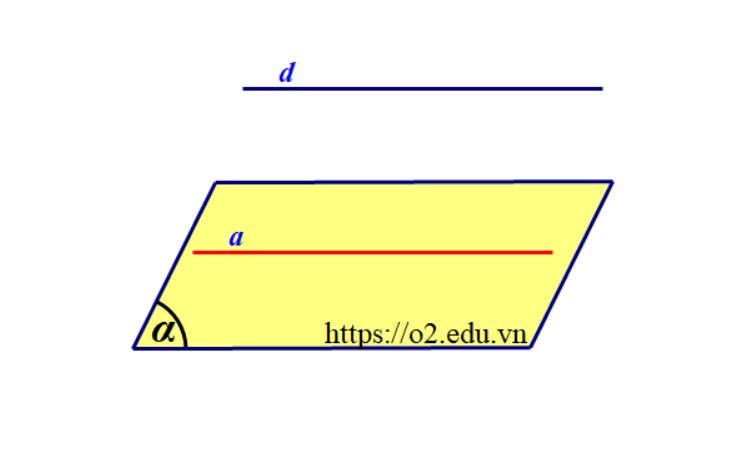
- Nếu một đường thẳng không nằm trên mặt phẳng mà song song với một đường thẳng của mặt phẳng đó thì đường thẳng đã cho song song với mặt phẳng đó. $$ begincases dnotsubset (alpha)\ dparallel a\ asubset (alpha) endcases Rightarrow d parallel (alpha)$$
- Nếu mặt phẳng $(alpha)$ chứa đường thẳng $d$ mà $ dparallel(beta) $ thì giao tuyến của hai mặt phẳng $(alpha)$ và $ (beta) $ cũng song song với đường thẳng $ d. $ $$ begincases d subset (alpha)\ d parallel (beta)\ b=(alpha) cap (beta) endcases Rightarrow d parallel b$$
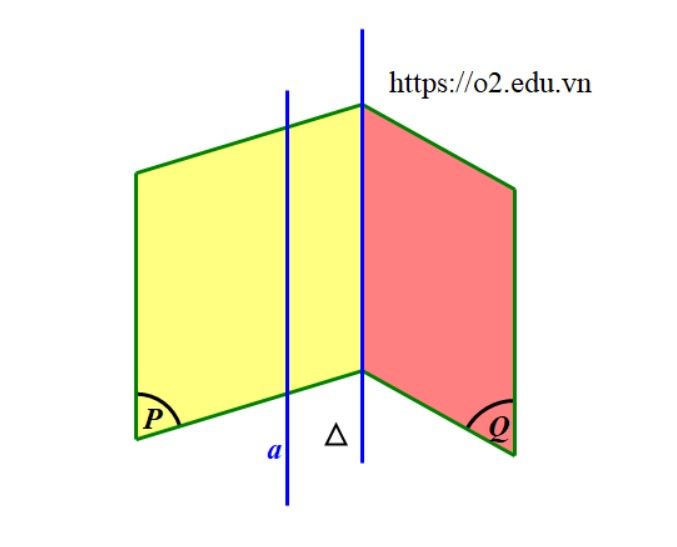
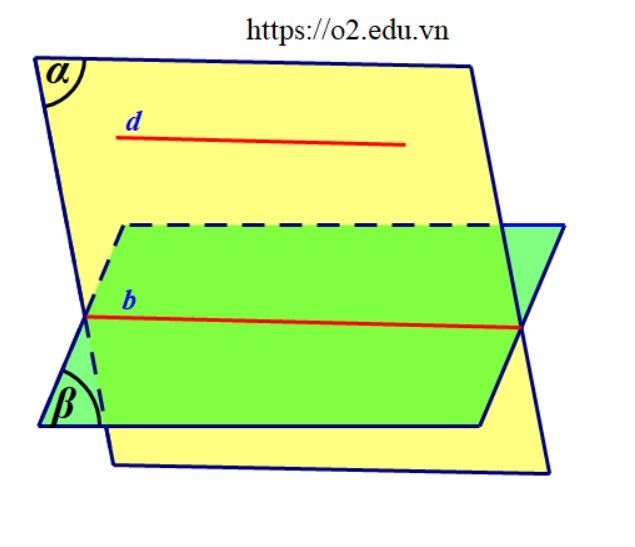Đặc biệt, nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó. $$ begincases (P) parallel a\ (Q.) parallel a\ Delta=(P) cap (Q.) endcases Rightarrow a parallel Delta$$
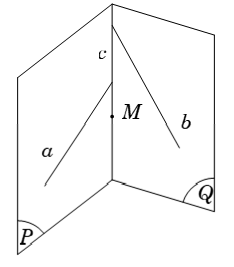
- Cho hai tuyến đường thẳng chéo nhau thì có duy nhất mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
2. Phương pháp chứng tỏ đường thẳng song song với mặt phẳng
Để chứng tỏ đường thẳng song song với mặt phẳng ta chứng tỏ đường thẳng đó không nằm trên mặt phẳng đã cho và song song với một đường thẳng của mặt phẳng đó.
3. Ví dụ cách đường thẳng song song với mặt phẳng
Ví dụ 1. Cho hình chóp $S.ABCD$ có $ M,N $ lần lượt là trung điểm của $ SA$ và $SB. $ Chứng minh rằng $ MNparallel(ABCD). $
Hướng dẫn. Vì $ MN $ là đường trung bình trong tam giác $ SAB $ nên $ MNparallel AB. $ Như vậy ta có [ begincases
MNnotsubset (ABCD)\ MNparallel ABsubset (ABCD) endcases ] Suy ra $ MNparallel(ABCD). $
Ví dụ 2. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành. Gọi $ M,N $ lần lượt là trung điểm của $ AB,CD $. Chứng minh rằng $ MNparallel(SBC),MNparallel(SAD). $ Gọi $ P $ là trung điểm $ SA, $ chứng tỏ rằng $ SB,SC $ cùng song song với mặt phẳng $ (MNP). $ Gọi $ G_1,G_2 $ lần lượt là trọng tâm tam giác $ ABC $ và $ SBC. $ Chứng minh rằng $ G_1G_2parallel(SAB).$
Hướng dẫn. Gọi $ O $ là tâm hình bình hành thì $ SCparallel PO. $ Gọi $ I $ là trung điểm $ BC $ và xét tam giác $ SAI $ có $ G_1G_2parallel SA. $
Ví dụ 3. Cho tứ diện $ABCD$ có $ G $ là trọng tâm tam giác $ ABD. $ Lấy điểm $ M $ thuộc cạnh $ BC $ sao cho $ MB=2MC. $ Chứng minh rằng $ MGparallel (ACD) $.
Hướng dẫn. Kéo dài $ BG $ cắt $ AD $ tại $ E $ thì $ (BMG)cap(ACD)=CE. $ Đi chứng tỏ $ MGparallel CE $ và suy ra điều phải chứng tỏ.
Ví dụ 4. Cho hai hình bình hành $ ABCD $ và $ ABEF $ không đồng phẳng. Chứng minh rằng bốn điểm $ C, D, E, F $ đồng phẳng. Gọi $ O, I $ là tâm những hình bình hành $ ABCD, ABEF $. Chứng minh rằng $ OIparallel (BCE), OI parallel (ADF). $ Gọi $ M, N $ lần lượt là trọng tâm tam giác $ ABD, ABF $. Chứng minh rằng $ MNparallel (CDFE) $.
Hướng dẫn. Chỉ ra $ MNparallel DF $ nên….
Ví dụ 5. Hai hình bình hành $ ABCD,ABEF $ có chung cạnh $ AB $ và không đồng phẳng. Trên những cạnh $ AD, BE $ lần lượt lấy những điểm $ M, N $ sao cho $fracAMAD=fracBNBE$. Chứng minh đường thẳng $ MN $ song song với mặt phẳng $ (CDFE) $.
Hướng dẫn. Trên $ CE $ lấy điểm $ P $ sao cho $ fracCPCE=fracBNBE $. Chứng minh tứ giác $ DMNP $ là hình bình hành. Từ đó suy ra $ MNparallel DP $ và có điều phải chứng tỏ.
Ví dụ 6. Cho hình chóp $ S.ABCD $ có $ ABCD $ là hình bình hành, $ G $ là trọng tâm của tam giác $ SAB $ và $ E $ là vấn đề trên cạnh $ AD $ sao cho $ DE = 2EA $. Chứng minh rằng $ GEparallel(SCD)$.
Hướng dẫn. Gọi $ H $ là trọng tâm tam giác $ SCD $ thì chứng tỏ được $ GEparallel HD. $
4. Bài tập chứng tỏ đường thẳng song song với mặt phẳng
Bài 1. Cho hình chóp $S.ABCD$ đáy là hình bình hành. Gọi $M, N, P$ lần lượt là trung điểm $AB, CD, SA.$ Chứng minh: $MN parallel (SBC); MN parallel (SAD)$; $SB parallel (MNP); SC parallel (MNP)$. Gọi $I, J$ là trọng tâm tam giác $ ACD,SCD $. Chứng minh: $IJ parallel (SAB), IJ parallel (SAD), IJ parallel (SAC).$
Bài 2. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O.$ Gọi $I, J$ là trung điểm $BC, SC$ và $ Kin SD$ sao cho $KD=2SK.$ Chứng minh: $OJ parallel (SAD), OJ parallel (SAB) $; $IO parallel (SCD), IJ parallel (SBD)$. Gọi $M$ là giao điểm của $AI$ và $BD$. Chứng minh: $MK parallel (SBC)$.
Bài 3. Cho hình chóp $S.ABCD$ có đáy là hình thoi tâm $O$ và $M, N, P$ là trung điểm $SB, SO, OD.$ Chứng minh: $MN parallel (ABCD), MO parallel (SCD)$; $NP parallel (SAD),$ tứ giác $ NPOM$ là hình gì? Gọi $Iin SD$ sao cho $SD = 4ID$. Chứng minh $PI parallel (SBC), PI parallel (SAB)$.
Đáp án: $B$
Giải thích tiến trình giải:
- Dựa vào hình ảnh ta thấy khi $(d)//(alpha)$ thì giữa chúng sẽ không còn điểm chung.
Tải app VietJack. Xem lời giải nhanh hơn! Quảng cáo
- Cho hai tuyến đường thẳng a và b. Căn cứ vào sự đồng phẳng và số điểm chung của hai tuyến đường thẳng ta có bốn trường hợp sau:
a. Hai đường thẳng song song: cùng nằm trong một mặt phẳng và không còn điểm chung, tức là:
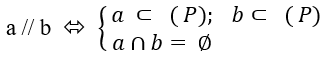
b. Hai đường thẳng cắt nhau: chỉ có một điểm chung: a cắt b ⇔ a ∩ b = I.
c. Hai đường thẳng trùng nhau: có hai điểm chung phân biệt: a ≡ b ⇔ a ∩ b = A; B
d. Hai đường thẳng chéo nhau: không cùng thuộc một mặt phẳng: a và b chéo nhau khi và chỉ khi a; b không đồng phẳng
- Hai đường thẳng song song
+ Tính chất 1: Trong không khí, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó
+ Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau
+ Định lí (về giao tuyến của hai mặt phẳng): Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song
+ Hệ quả: Nếu hai mặt phẳng lần lượt đi qua hai tuyến đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai tuyến đường thẳng đó (hoặc trùng với một trong hai tuyến đường thẳng đó)
Ví dụ 1: Trong những mệnh đề sau; mệnh đề nào sai ?
A. Hai đường thẳng không còn điểm chung thì chéo nhau
B. Hai đường thẳng chéo nhau thì không còn điểm chung
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song
Lời giải:
Hai đường thẳng không còn điểm chung thì chúng song song (khi chúng đồng phẳng) hoặc chéo nhau (khi chúng không đồng phẳng)
Chọn A
Ví dụ 2: Tìm mênh đề đúng trong những mệnh đề sau:
A. Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác
B. Hai đường thẳng song song khi và chỉ khi chúng không còn điểm chung
C. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng
D. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng
Quảng cáo
Lời giải:
Chọn D
- A sai. Trong trường hợp 2 đường thẳng cắt nhau thì chúng chỉ có một điểm chung
- B và C sai. Hai đường thẳng song song khi và chỉ khi chúng đồng phẳng và không còn điểm chung
Ví dụ 3: Tìm mệnh đề đúng trong những mệnh đề sau:
A. Hai đường thẳng cùng song song với đường thẳng thứ ban thì song song với nhau.
B. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai tuyến đường thẳng đó song song hoặc trùng với nhau
D. Tất cả sai
Lời giải:
Chọn C
Ví dụ 4: Tìm mệnh đề đúng?
A. Hai đường thẳng chéo nhau khi và chỉ khi chúng có ít hơn 2 điểm chung.
B. Hai đường thẳng không còn điểm chung là 2 đường thẳng song song hoặc chéo nhau.
C. Hai đường thẳng song song với nhau nếu chúng đồng phẳng.
D. Khi 2 đường thẳng phân biệt nằm trên 2 mặt phẳng phân biệt thì hai tuyến đường thẳng đó chéo nhau.
Lời giải:
Chọn B.
- A sai. Hai đường thẳng chéo nhau thì chúng không còn điểm chung. Hai đường thẳng có một điểm chung duy nhất thì 2 đường thẳng đó cắt nhau.
- C sai. Có thể xảy ra trường hợp hai tuyến đường thẳng đó hoặc cắt nhau hoặc trùng nhau.
- D sai. Có thể xảy ra trường hợp hai tuyến đường thẳng đó song song.
Ví dụ 5: Cho 2 đường thẳng chéo nhau a và b. Lấy A; B thuộc a và C; D thuộc b. Khẳng định nào sau đây đúng khi nói về 2 đường thẳng AD và BC
A. Có thể song song hoặc cắt nhau
B. Cắt nhau
C. Song song với nhau
D. Chéo nhau
Lời giải:
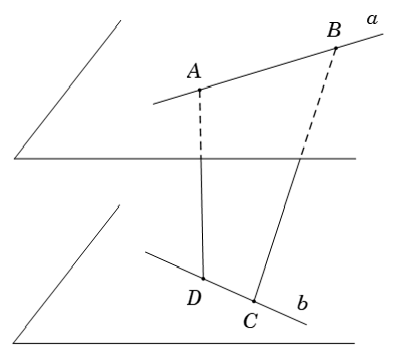
Theo giả thiết, a và b chéo nhau nên a và b không đồng phẳng
Giả sử AD và BC đồng phẳng
- Nếu AD cắt BC tại I thì I ∈ (ABCD) nên I ∈ (a; b)
Mà a và b không đồng phẳng, do đó, không tồn tại điểm I
- Nếu AD // BC thì a và đồng phẳng (Mâu thuẫn với giả thiết)
Vậy điều giả sử là sai. Do đó AD và BC chéo nhau.
Chọn D.
Quảng cáo
Ví dụ 6: Cho 3 mặt phẳng (P); (Q.) và (R). Nếu (P) ∩ (Q.) = a; (P) ∩ (R) = b và (Q.) ∩ (R) = c. Khi đó 3 đường thẳng a; b; c sẽ:
A. Đôi một cắt nhau
B. Đôi một song song
C. Đồng quy
D. Song song hoặc đồng quy với nhau
Lời giải:
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyền ấy hoặc đồng quy hoặc đôi một song song
Chọn D
Ví dụ 7: Chọn mệnh đề đúng trong những mệnh đề sau:
A. Hai đường thẳng không còn điểm chung thì chéo nhau.
B. Hai đường thẳng phân biệt không còn điểm chung thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không còn điểm chung.
D. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
Lời giải:
Chọn C.
Câu A sai vì hai tuyến đường thẳng không còn điểm chung thì chéo nhau hoặc song song với nhau.
Câu B sai vì hai tuyến đường thẳng phân biệt không còn điểm chung thì chéo nhau hoặc song song với nhau.
Câu D sai vì hai tuyến đường thẳng phân biệt nằm trên hai mặt phẳng phân biệt thì hoàn toàn có thể chéo nhau hoặc song song với nhau.
Ví dụ 8: Hãy Chọn Câu đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng song song nhau nếu chúng không còn điểm chung.
C. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.
D. Không xuất hiện phẳng nào chứa cả hai tuyến đường thẳng a và b thì ta nói a và b chéo nhau.
Lời giải:
Chọn D
- Hai đường thẳng cùng song song với một đường thẳng thứ ba thì hoàn toàn có thể trùng nhau ⇒ A sai.
- Hai đường thẳng không còn điểm chung thì song song hoặc chéo nhau ⇒ B sai.
- Hai đường thẳng cùng song song với một mặt phẳng thì hoàn toàn có thể cắt, trùng hoặc chéo nhau ⇒ C sai.
- Hai đường thẳng chéo nhau nếu chúng không đồng phẳng ⇒ D đúng.
Ví dụ 9: Hãy Chọn Câu đúng?
A. Nếu ba mặt phẳng cắt nhau theo ba giao tuyến thì ba giao tuyến đó đồng qui.
B. Nếu hai mặt phẳng lần lượt chứa hai tuyến đường thẳng song song thì giao tuyến, nếu có, của chúng sẽ song song với cả hai tuyến đường thẳng đó.
C. Nếu hai tuyến đường thẳng a và b chéo nhau thì có hai tuyến đường thẳng p và q song song nhau mà mỗi đường đều cắt cả a và b .
D. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
Lời giải:
Chọn D.
- Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì hoàn toàn có thể đôi một song song nhau
Suy ra A sai.
- Nếu hai mặt phẳng lần lượt chứa hai tuyến đường thẳng song song thì giao tuyến, nếu có, của chúng hoàn toàn có thể trùng với một trong hai tuyến đường thẳng đó ⇒ B sai.
- Giả sử: p cắt a và b lần lượt tại A và B; q cắt a và b lần lượt tại A’ và B’.
Nếu p // q ⇒ A; B; A’ và B’ đồng phẳng ⇒ a; b đồng phẳng (xích míc) ⇒ C sai.
- Hai đường thẳng chéo nhau nếu chúng không đồng phẳng ⇒ D đúng
Ví dụ 10: Cho hai tuyến đường thẳng phân biệt a và b cùng thuộc mp(α). Có bao nhiêu vị trí tương đối giữa a và b?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Chọn C
Vị trí tương đối của hai tuyến đường thẳng phân biệt cùng nằm trong 1 mặt phẳng là:
+ Hai đường thẳng cắt nhau.
+ Hai đường thẳng song song.
Chú ý : Đây là hai tuyến đường thẳng phân biệt nên không xảy ra trường hợp hai tuyến đường thẳng trùng nhau.
Ví dụ 11: Cho hai tuyến đường thẳng chéo nhau a và b. Lấy A, B thuộc a và C, D thuộc b. Khẳng định nào sau đây đúng khi nói về hai tuyến đường thẳng AD và BC?
A. Có thể song song hoặc cắt nhau
B. Cắt nhau
C. Song song nhau
D. Chéo nhau
Lời giải:
Chọn D
Ta có a và b chéo nhau nên hai tuyến đường thẳng AB và CD chéo nhau
⇒ Bốn điểm A ; B ; C ; D không đồng phẳng. Khi đó 4 điểm này là 4 đỉnh của một tứ diện.
Do đó AD và BC chéo nhau
Câu 1: Trong không khí, cho 3 đường thẳng a; b; c biết a // b; hai tuyến đường thẳng a và c chéo nhau. Khi đó; 2 đường thẳng b và c:
A. Trùng nhau hoặc chéo nhau
B. Cắt nhau hoặc chéo nhau
C. Chéo nhau hoặc song song
D. Song song hoặc trùng nhau.
Hiển thị lời giải
Giả sử b // c
Theo giả thiết: a // b
⇒ a // c (xích míc với giả thiết)
Chọn B
Câu 2: Trong không gianl cho 3 đường thẳng phân biệt a; b; c trong đó a // b. Tìm mệnh đề sai?
A. Nếu a // c thì b // c
B. Nếu c cắt a thì c cắt b
C. Nếu A ∈ a; B ∈ b thì 3 đường thẳng a; b; AB cùng thuộc một mặt phẳng
D. Tồn tại duy nhất một mặt phẳng chứa a và b
Hiển thị lời giải
Nếu đường thẳng c cắt a thì c cắt b hoặc c chéo b
Chọn B
Câu 3: Cho 2 đường thẳng chéo nhau a và b; điểm M không thuộc hai tuyến đường thẳng trên. Có nhiểu nhất bao nhiêu đường thẳng qua M cắt cả a và b
A. 1 B. 2 C. 0 D. Vô số.
Hiển thị lời giải
Gọi (P) là mặt phẳng tạo bởi đường thẳng a và M
(Q.) là mặt phẳng tạo bởi đường thẳng b và M.
Giả sử c là đường thẳng qua M cắt cả a và b.
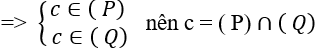
Vậy chỉ có một đường thẳng qua M cắt cả a và b
Chọn A
Câu 4: Trong không khí; cho 3 đường thẳng a; b; c đôi một chéo nhau. Có nhiều nhất bao nhiêu đường thẳng cắt cả 3 đường thẳng này?
A. 1 B. 2 C. 0 D. Vô số
Hiển thị lời giải
+ Gọi M là vấn đề bất kì nằm trên a
+ Giả sử d là đường thẳng qua M cắt cả b và c. Khi đó, d là giao tuyến của mặt phẳng (M; b) với mặt phẳng (M; c)
+ Với mỗi điểm M ta được một đường thẳng d
Vậy có vô số đường thẳng cắt cả 3 đường thẳng a; b; c
Chọn D
Câu 5: Trong không khí, cho đường thẳng d và điểm M nằm ngoài đường thẳng d. Chọn mệnh đề đúng?
A. Có vô số đường thẳng qua M và song song với đường thẳng d
B. Có vô số đường thẳng qua M và cắt d
C. Cả A và B đúng
D. Tất cả sai
Hiển thị lời giải
+ Qua điểm M nằm ngoài đường thẳng d có duy nhất một đường thẳng song song với d
⇒ A sai
+ Qua M có vô số đường thẳng cắt d. Đó là những đường thẳng nối M và một điểm bất kì nằm trên đường thẳng d
⇒ B đúng
Chọn B
Câu 6: Trong những mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng chéo nhau khi chúng không còn điểm chung.
B. Hai đường thẳng không còn điểm chung là hai tuyến đường thẳng song song hoặc chéo nhau.
C. Hai đường thẳng song song nhau khi chúng ở trên cùng một mặt phẳng.
D. Khi hai tuyến đường thẳng ở trên hai mặt phẳng thì hai tuyến đường thẳng đó chéo nhau.
Hiển thị lời giải
Chọn B
Dựa vào vị trí tương đối giữa hai tuyến đường thẳng:
+ Hai đường thẳng có đúng 1 điểm chung thì hai tuyến đường thẳng đó cắt nhau.
+ Hai đường thẳng có vô số điềm chung thì hai tuyến đường thẳng đó trùng nhau.
+ Hai đường thẳng không còn điểm chung nếu chúng song song hoặc chéo nhau.
Câu 7: Trong những mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
B. Hai đường thẳng không còn điểm chung thì chéo nhau
C. Hai đường thẳng chéo nhau thì không còn điểm chung
D. Hai đường thẳng phân biệt không song song thì chéo nhau
Hiển thị lời giải
Chọn C
Ta xét những phương án:
+ Phương án A: Hai đường đường thẳng nằm trên hai mặt phẳng phân biệt thì hoàn toàn có thể trùng nhau; cắt nhau hoặc song song. Ví dụ: Hình chóp S.ABCD có mp(SAB)và (ABCD) có chung đường thẳng AB.
⇒ A sai
+ Phương án B: Hai đường thẳng không còn điểm chung thì hoàn toàn có thể song song hoặc chéo nhau.
⇒ B sai
+ Phương án C: Hai đường thẳng chéo nhau thì không còn điểm chung
⇒ C đúng
+ Phương án D: Hai đường thẳng phân biệt không song song thì hoàn toàn có thể cắt nhau hoặc chéo nhau.
⇒ D sai
Câu 8: Trong không khí, cho ba đường thẳng phân biệt a , b và c trong đó a // b. Khẳng định nào sau đây không đúng?
A. Nếu a // c thì b // c
B. Nếu c cắt a thì c cắt b
C. Nếu A ∈ a và B ∈ b thì ba đường thẳng a, b, AB cùng ở trên một mặt phẳng
D. Tồn tại duy nhất một mặt phẳng qua a và b
Hiển thị lời giải
Chọn B
Phương án B sai do a, c cắt nhau nên cùng nằm trong mp(α) và đường thẳng b song song với (α)
Khi đó c và b hoàn toàn có thể chéo nhau.
Câu 9: Cho đường thẳng a nằm trên mp(P) đường thẳng b cắt (P) tại O và O không thuộc a. Vị trí tương đối của a và b là
A. chéo nhau
B. cắt nhau
C. song song nhau
D. trùng nhau
Hiển thị lời giải
Chọn A
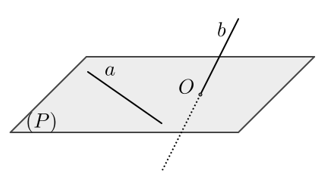
Dựa vào hình vẽ trên ta suy ra a và b chéo nhau.
Xem thêm những dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù phù hợp với nội quy phản hồi trang web sẽ bị cấm phản hồi vĩnh viễn.
duong-thang-va-mat-phang-trong-khong-gian-quan-he-song-song.jsp
[embed]https://www.youtube.com/watch?v=NOEVFr6KgUs[/embed]