Mẹo về Đường thẳng a song song với mặt phẳng (P nếu) Mới Nhất
Bùi Phương Thảo đang tìm kiếm từ khóa Đường thẳng a song song với mặt phẳng (P nếu) được Cập Nhật vào lúc : 2022-03-26 12:41:19 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.
VnHocTap.com ra mắt đến những em học viên lớp 11 nội dung bài viết Chứng minh đường thẳng a song song với mặt phẳng (P), nhằm mục đích giúp những em học tốt chương trình Toán 11.
Nội dung chính- 1. Vị trí tương đối của đường thẳng và mặt phẳngĐịnh nghĩa đường thẳng và mặt phẳng song song.Tính chất của đường thẳng và mặt phẳng song song.2. Phương pháp chứng tỏ đường thẳng song song với mặt phẳng3. Ví dụ cách đường thẳng song song với mặt phẳng4. Bài tập chứng tỏ đường thẳng song song với mặt phẳngVideo liên quan
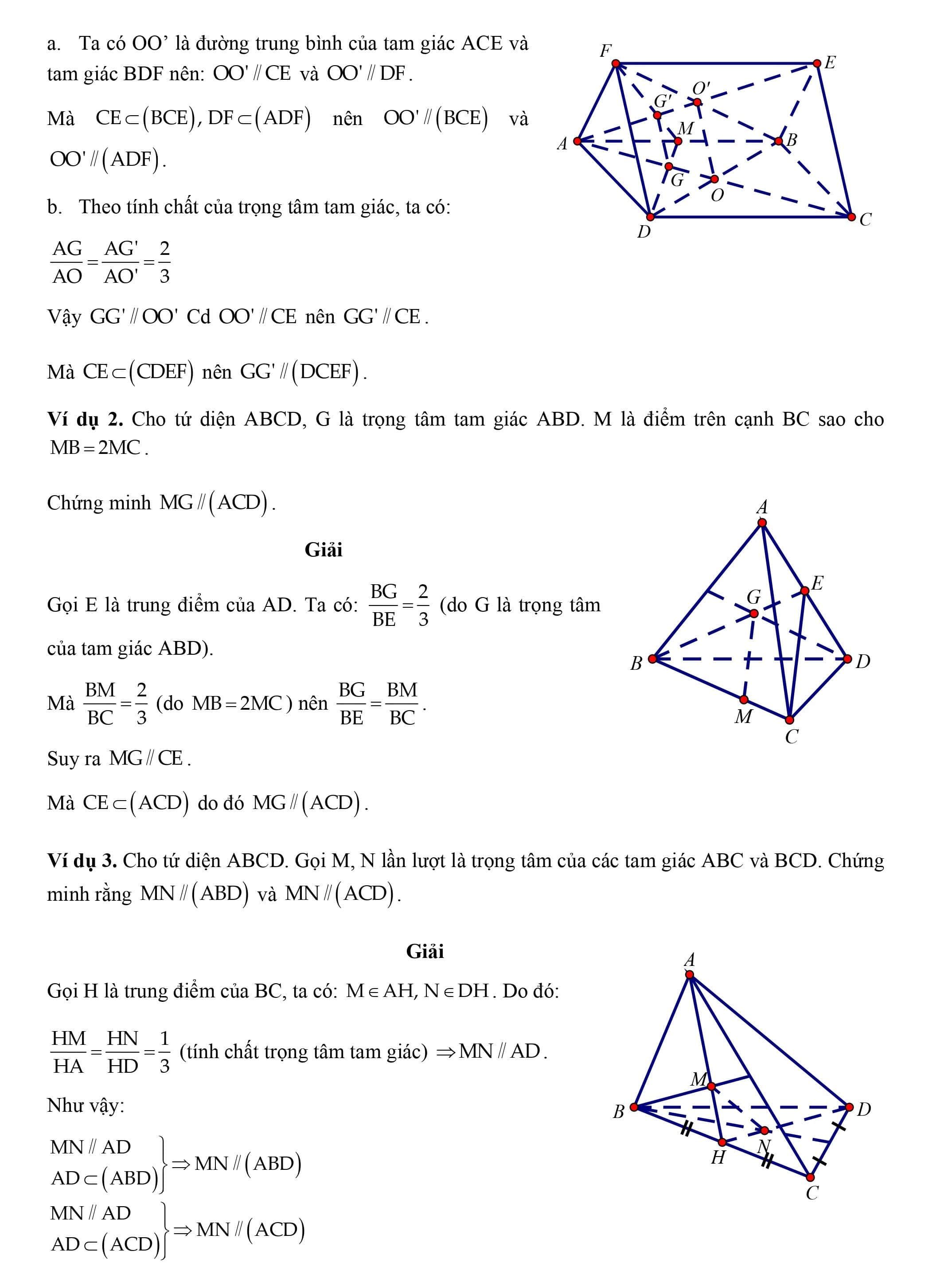
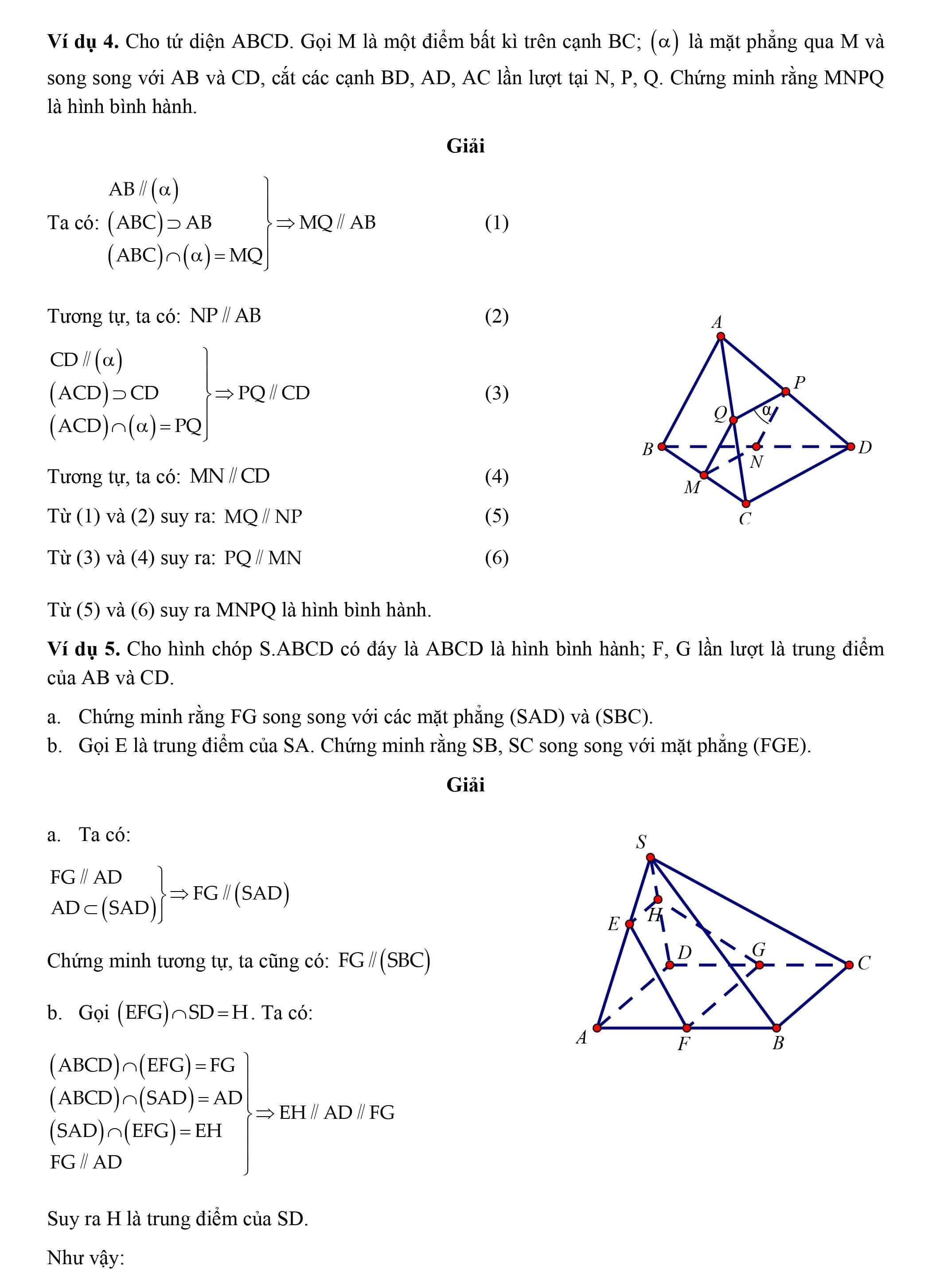
Nội dung nội dung bài viết Chứng minh đường thẳng a song song với mặt phẳng (P): Chứng minh đường thẳng a song song với mặt phẳng (P). Phương pháp (Dùng định lí 1). Nếu không còn sẵn đường thẳng b trong mặt phẳng (P) thì ta tìm đường thẳng b bằng phương pháp chọn một mặt phẳng (Q.) chứa a và cắt (P), giao tuyến của (P) và (Q.) đó đó là đường thẳng b cần tìm. Các ví dụ. Ví dụ 1. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O và O’ lần lượt là tâm của hai hình bình hành ABCD và ABEF. a. Chứng minh OO’ song song với những mặt phẳng (ADF) và (BCE). b. Gọi G và G’ lần lượt là trọng tâm những tam giác ABD và ABF. Chứng minh GG’ // (DCEF). Ta có OO’ là đường trung bình của tam giác ACE và tam giác BDF nên: OO’ // CE và OO’ // DF. b. Theo tính chất của trọng tâm tam giác. Ví dụ 2. Cho tứ diện ABCD, G là trọng tâm tam giác ABD. M là vấn đề trên cạnh BC sao cho MB = 2MC. Gọi E là trung điểm của AD. G là trọng tâm của tam giác ABD mà BN = (do MB = 2MC). Suy ra MG // CE. Ví dụ 3. Cho tứ diện ABCD. Gọi M, N lần lượt là trọng tâm của những tam giác ABC và BCD. Chứng minh rằng MN // (ABD) và MN (ACD). Gọi H là trung điểm của BC. Ví dụ 4. Cho tứ diện ABCD. Gọi M là một điểm bất kì trên cạnh BC; (a) là mặt phẳng qua M và song song với AB và CD, cắt những cạnh BD, AD, AC lần lượt tại N, P, Q.. Chứng minh rằng MNPQ là hình bình hành. MNPQ là hình bình hành.
Ví dụ 5. Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành; F, G lần lượt là trung điểm của AB và CD. a. Chứng minh rằng FG song song với những mặt phẳng (SAD) và (SBC). b. Gọi E là trung điểm của SA. Chứng minh rằng SB, SC song song với mặt phẳng (FGE). Ví dụ 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (a) là mặt phẳng đi qua trung điểm M của cạnh SB, song song với cạnh AB, cắt những cạnh SA, SD, SC lần lượt tại Q., P và N. Hãy xác định hình tính của tứ giác MNPQ?
- Nếu đường thẳng (a) không nằm trên mặt phẳng ((P)) và song song với một đường thẳng (b) nào đó nằm trên mặt phẳng ((P)) thì (a) song song với ((P)).
Kí hiệu:
(left{ beginarrayla notsubset (P)\b subset (P)\a,;//;b
endarray right.;;; Rightarrow a;//;(P).)
- Nếu đường thẳng (a) song song với mặt phẳng ((P)) thì mọi mặt phẳng ((Q.)) chứa (a) mà cắt ((P)) thì cắt ((P)) theo giao tuyến song song với (a). (Đây là tính chất quan trọng dùng để xác định giao tuyến hai mặt phẳng và để tìm thiết diện của hình chóp).
Kí hiệu:
(left{ beginarrayla;//;(P)\(Q.) supset a\(P) cap (Q.) = b
endarray right.;;;; Rightarrow a;//;b.)
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Kí hiệu:
(left{ beginarrayl(P)//;a\(Q.)//;a\(P) cap (Q.) = b
endarray right.;;; Rightarrow a;//;b.)
- Nếu (a) và (b) là hai tuyến đường thẳng chéo nhau thì có duy nhất một mặt phẳng chứa (a) và song song với (b).
Loigiaihay.com
Thành thạo cách chứng tỏ đường thẳng song song với mặt phẳng sẽ giúp những em học viên hoàn toàn có thể chứng tỏ được hai mặt phẳng song song với nhau.
Xem thêm 3 cách chứng tỏ hai mặt phẳng song song
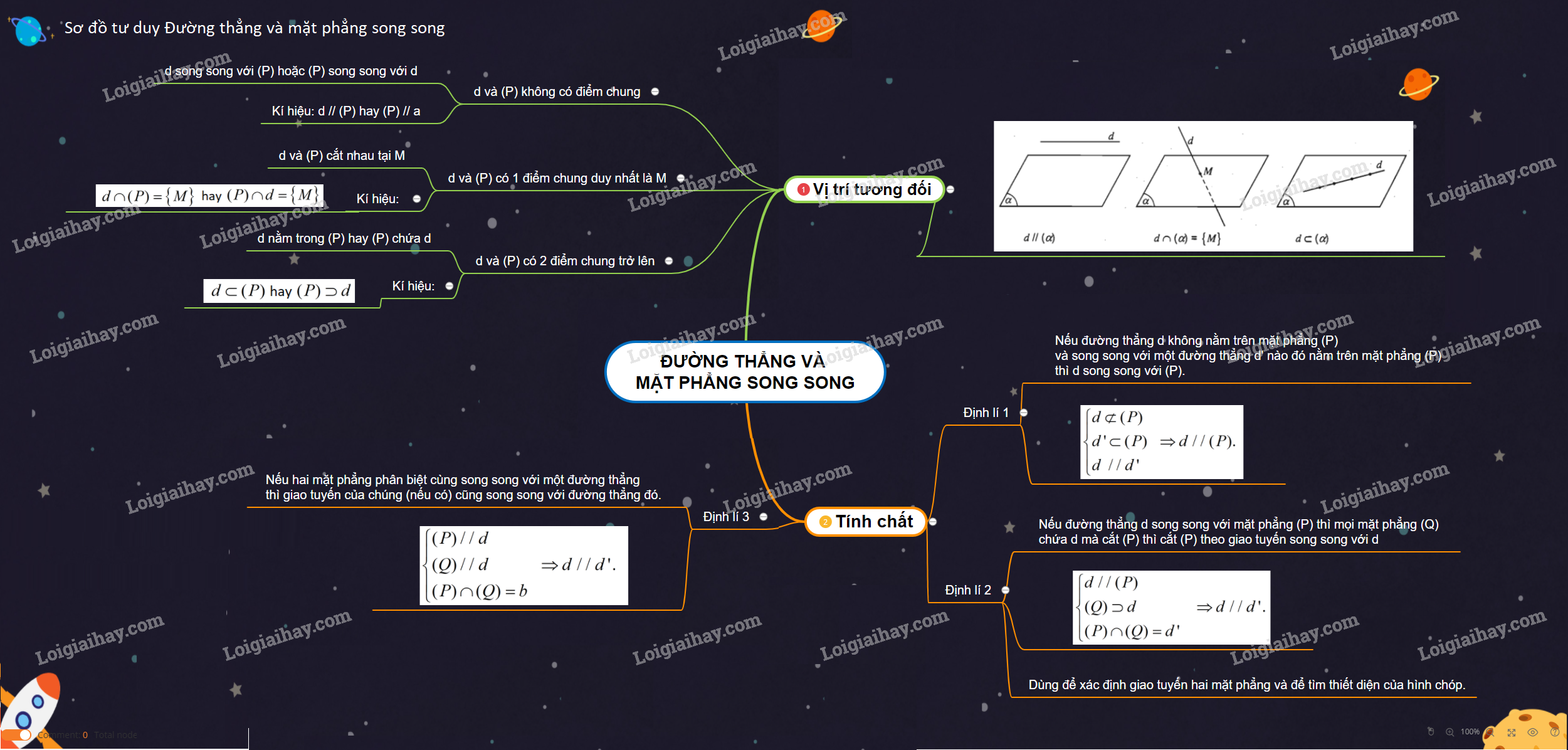
1. Vị trí tương đối của đường thẳng và mặt phẳng
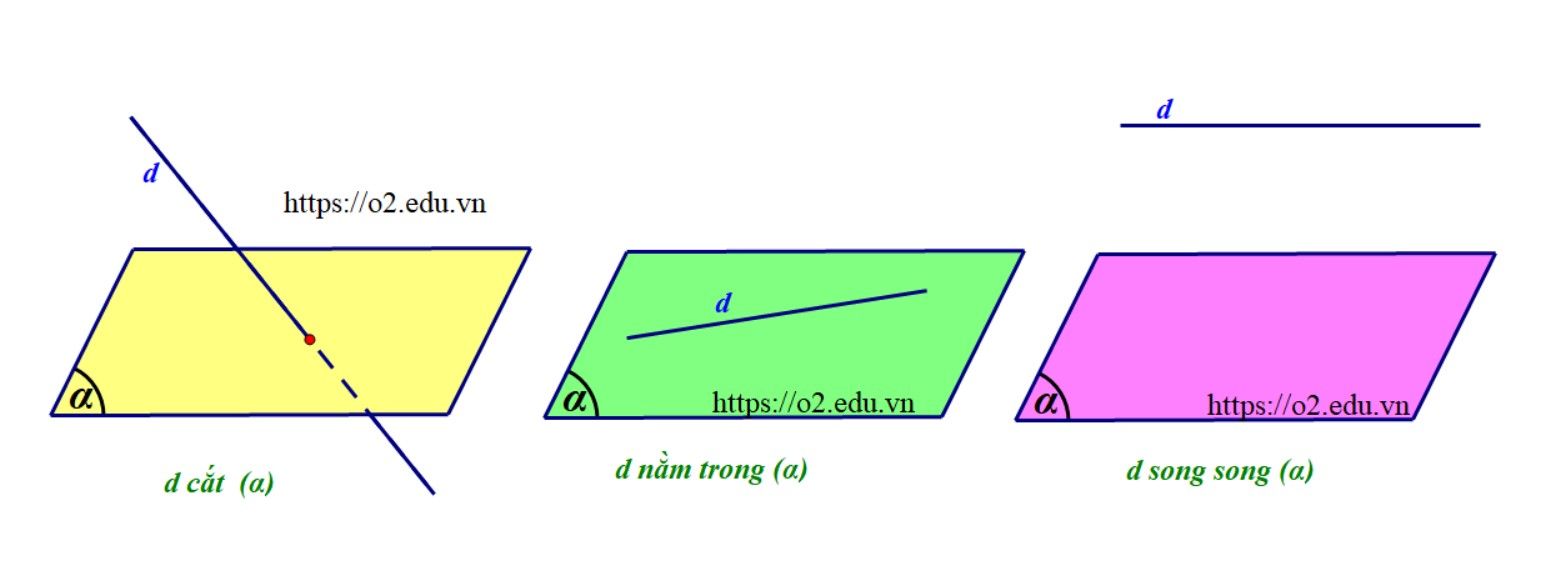
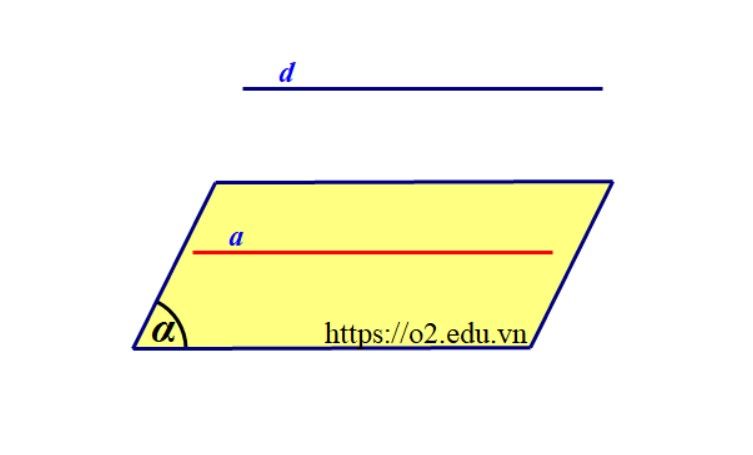
Trong không khí, xét một đường thẳng $d$ và mặt phẳng $(alpha)$ thì có ba kĩ năng về vị trí giữa chúng:
- Đường thẳng $d$ cắt $ (alpha) $: có một điểm chung.
Đường thẳng $d$ nằm trên $ (alpha) $: có vô số điểm chung.
Đường thẳng $ d $ song song $ (alpha) $: không còn điểm chung.
Định nghĩa đường thẳng và mặt phẳng song song.
Đường thẳng và mặt phẳng được gọi là song song nếu chúng không còn điểm chung.
Tính chất của đường thẳng và mặt phẳng song song.
- Nếu một đường thẳng không nằm trên mặt phẳng mà song song với một đường thẳng của mặt phẳng đó thì đường thẳng đã cho song song với mặt phẳng đó. $$ begincases dnotsubset (alpha)\ dparallel a\ asubset (alpha) endcases Rightarrow d parallel (alpha)$$
- Nếu mặt phẳng $(alpha)$ chứa đường thẳng $d$ mà $ dparallel(beta) $ thì giao tuyến của hai mặt phẳng $(alpha)$ và $ (beta) $ cũng song song với đường thẳng $ d. $ $$ begincases d subset (alpha)\ d parallel (beta)\ b=(alpha) cap (beta) endcases Rightarrow d parallel b$$
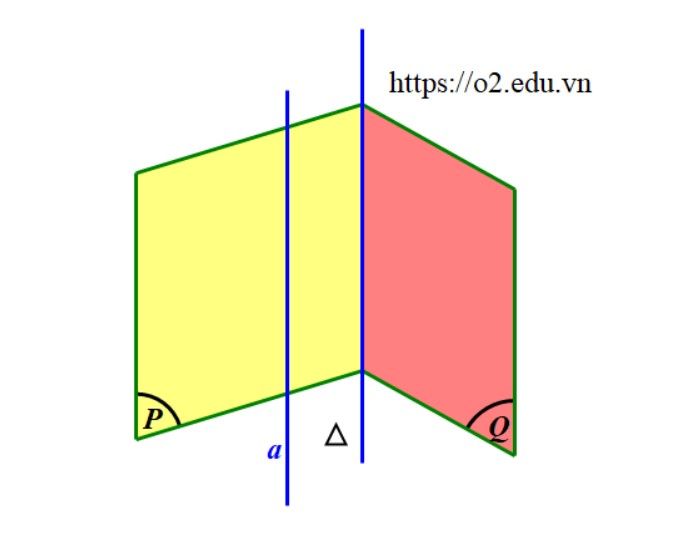
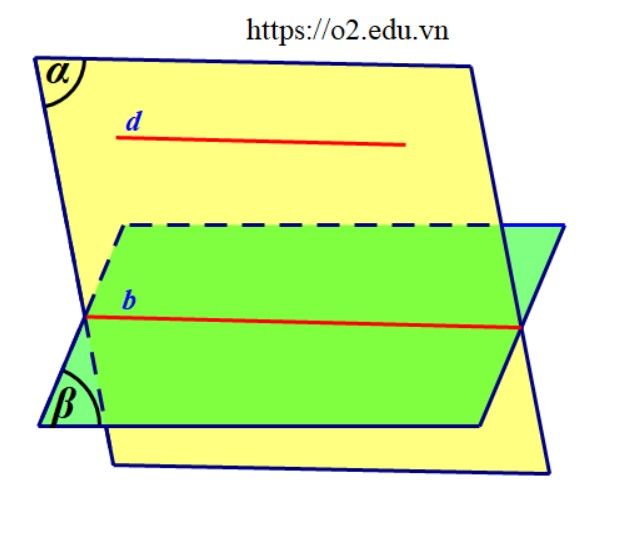Đặc biệt, nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó. $$ begincases (P) parallel a\ (Q.) parallel a\ Delta=(P) cap (Q.) endcases Rightarrow a parallel Delta$$
- Cho hai tuyến đường thẳng chéo nhau thì có duy nhất mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
2. Phương pháp chứng tỏ đường thẳng song song với mặt phẳng
Để chứng tỏ đường thẳng song song với mặt phẳng ta chứng tỏ đường thẳng đó không nằm trên mặt phẳng đã cho và song song với một đường thẳng của mặt phẳng đó.
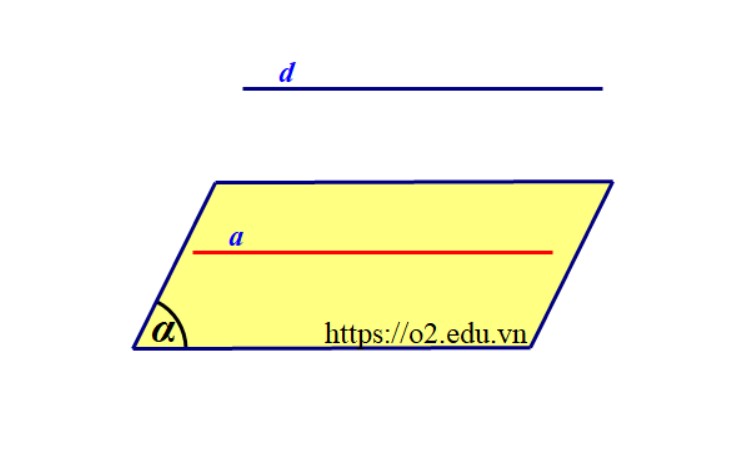
3. Ví dụ cách đường thẳng song song với mặt phẳng
Ví dụ 1. Cho hình chóp $S.ABCD$ có $ M,N $ lần lượt là trung điểm của $ SA$ và $SB. $ Chứng minh rằng $ MNparallel(ABCD). $
Hướng dẫn. Vì $ MN $ là đường trung bình trong tam giác $ SAB $ nên $ MNparallel AB. $ Như vậy ta có [ begincases
MNnotsubset (ABCD)\ MNparallel ABsubset (ABCD) endcases ] Suy ra $ MNparallel(ABCD). $
Ví dụ 2. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành. Gọi $ M,N $ lần lượt là trung điểm của $ AB,CD $. Chứng minh rằng $ MNparallel(SBC),MNparallel(SAD). $ Gọi $ P $ là trung điểm $ SA, $ chứng tỏ rằng $ SB,SC $ cùng song song với mặt phẳng $ (MNP). $ Gọi $ G_1,G_2 $ lần lượt là trọng tâm tam giác $ ABC $ và $ SBC. $ Chứng minh rằng $ G_1G_2parallel(SAB).$
Hướng dẫn. Gọi $ O $ là tâm hình bình hành thì $ SCparallel PO. $ Gọi $ I $ là trung điểm $ BC $ và xét tam giác $ SAI $ có $ G_1G_2parallel SA. $
Ví dụ 3. Cho tứ diện $ABCD$ có $ G $ là trọng tâm tam giác $ ABD. $ Lấy điểm $ M $ thuộc cạnh $ BC $ sao cho $ MB=2MC. $ Chứng minh rằng $ MGparallel (ACD) $.
Hướng dẫn. Kéo dài $ BG $ cắt $ AD $ tại $ E $ thì $ (BMG)cap(ACD)=CE. $ Đi chứng tỏ $ MGparallel CE $ và suy ra điều phải chứng tỏ.
Ví dụ 4. Cho hai hình bình hành $ ABCD $ và $ ABEF $ không đồng phẳng. Chứng minh rằng bốn điểm $ C, D, E, F $ đồng phẳng. Gọi $ O, I $ là tâm những hình bình hành $ ABCD, ABEF $. Chứng minh rằng $ OIparallel (BCE), OI parallel (ADF). $ Gọi $ M, N $ lần lượt là trọng tâm tam giác $ ABD, ABF $. Chứng minh rằng $ MNparallel (CDFE) $.
Hướng dẫn. Chỉ ra $ MNparallel DF $ nên….
Ví dụ 5. Hai hình bình hành $ ABCD,ABEF $ có chung cạnh $ AB $ và không đồng phẳng. Trên những cạnh $ AD, BE $ lần lượt lấy những điểm $ M, N $ sao cho $fracAMAD=fracBNBE$. Chứng minh đường thẳng $ MN $ song song với mặt phẳng $ (CDFE) $.
Hướng dẫn. Trên $ CE $ lấy điểm $ P $ sao cho $ fracCPCE=fracBNBE $. Chứng minh tứ giác $ DMNP $ là hình bình hành. Từ đó suy ra $ MNparallel DP $ và có điều phải chứng tỏ.
Ví dụ 6. Cho hình chóp $ S.ABCD $ có $ ABCD $ là hình bình hành, $ G $ là trọng tâm của tam giác $ SAB $ và $ E $ là vấn đề trên cạnh $ AD $ sao cho $ DE = 2EA $. Chứng minh rằng $ GEparallel(SCD)$.
Hướng dẫn. Gọi $ H $ là trọng tâm tam giác $ SCD $ thì chứng tỏ được $ GEparallel HD. $
4. Bài tập chứng tỏ đường thẳng song song với mặt phẳng
Bài 1. Cho hình chóp $S.ABCD$ đáy là hình bình hành. Gọi $M, N, P$ lần lượt là trung điểm $AB, CD, SA.$ Chứng minh: $MN parallel (SBC); MN parallel (SAD)$; $SB parallel (MNP); SC parallel (MNP)$. Gọi $I, J$ là trọng tâm tam giác $ ACD,SCD $. Chứng minh: $IJ parallel (SAB), IJ parallel (SAD), IJ parallel (SAC).$
Bài 2. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O.$ Gọi $I, J$ là trung điểm $BC, SC$ và $ Kin SD$ sao cho $KD=2SK.$ Chứng minh: $OJ parallel (SAD), OJ parallel (SAB) $; $IO parallel (SCD), IJ parallel (SBD)$. Gọi $M$ là giao điểm của $AI$ và $BD$. Chứng minh: $MK parallel (SBC)$.
Bài 3. Cho hình chóp $S.ABCD$ có đáy là hình thoi tâm $O$ và $M, N, P$ là trung điểm $SB, SO, OD.$ Chứng minh: $MN parallel (ABCD), MO parallel (SCD)$; $NP parallel (SAD),$ tứ giác $ NPOM$ là hình gì? Gọi $Iin SD$ sao cho $SD = 4ID$. Chứng minh $PI parallel (SBC), PI parallel (SAB)$.
[embed]https://www.youtube.com/watch?v=cOEs8xe77OA[/embed]