Kinh Nghiệm về Chỗ tứ giác ABCD có góc A bằng 120 độ góc B bằng 80 độ góc C bằng 110 độ Tính góc D 2022
Dương Khoa Vũ đang tìm kiếm từ khóa Chỗ tứ giác ABCD có góc A bằng 120 độ góc B bằng 80 độ góc C bằng 110 độ Tính góc D được Update vào lúc : 2022-04-20 04:11:10 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.1. Cho tứ giác ABCD có góc B=120 độ, góc C =60 độ, góc D=90 độ. Tính góc A góc ngoài tại đỉnh A.
Vẽ hình và làm bài nhanh hộ mik!!!!!
 Tải app VietJack. Xem lời giải nhanh hơn!
Tải app VietJack. Xem lời giải nhanh hơn! Quảng cáo
Để tính góc giữa hai tuyến đường thẳng d1; d2 trong không khí ta hoàn toàn có thể thực hiện theo hai cách
Cách 1. Tìm góc giữa hai tuyến đường thẳng d1, d2 bằng phương pháp chọn một điểm O thích hợp (O thường nằm trên một trong hai tuyến đường thẳng).

Lưu ý 1: Để tính góc này ta thường sử dụng định lí côsin trong tam giác
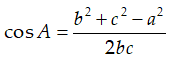
Cách 2. Tìm hai vec tơ chỉ phương u1, u2 của hai tuyến đường thẳng d1, d2
Khi đó góc giữa hai tuyến đường thẳng d1, d2 xác định bởi cos(d1, d2) = 
Lưu ý 2: Để tính u1→, u2→, |u1→|, |u2→| ta chọn ba vec tơ a→, b→, c→ không đồng phẳng mà hoàn toàn có thể tính được độ dài và góc giữa chúng,sau đó biểu thị những vec tơ u1→, u2→ qua những vec tơ a→, b→, c→ rồi thực hiện những tính toán.
Ví dụ 1: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB→ và DH→
A. 45° B. 90° C. 120° D.60°
Quảng cáo
Hướng dẫn giải:
Vì DH→ = AE→ ( ADHE là hình vuông vắn) nên (AB→, DH→) = (AB→, AE→) = ∠BAE = 90° (ABFE là hình vuông vắn).
Chọn B
Ví dụ 2: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB→ và EG→?
A. 90° B. 60° C. 45° D. 120°
Hướng dẫn giải
Vì EG→ = AC→ ( tứ giác AEGC là hình chữ nhật) nên:
 (do ABCD là hình vuông vắn)
(do ABCD là hình vuông vắn)
Chọn C.
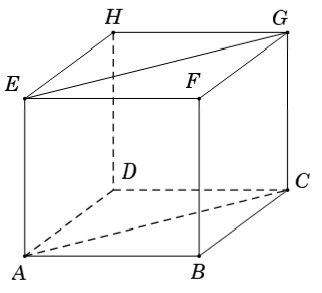
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa AC và DA’ là:
A. 45° B. 90° C. 60° D. 120°
Hướng dẫn giải
Gọi a là độ dài cạnh hình lập phương
Khi đó, tam giác AB’C đều (AB' = B'C = CA = a√2) do đó ∠B'CA= 60° .
Lại có, DA’ song song CB’ nên
(AC, DA') = (AC, CB') = ∠ACB'= 60°.
Chọn C
Quảng cáo
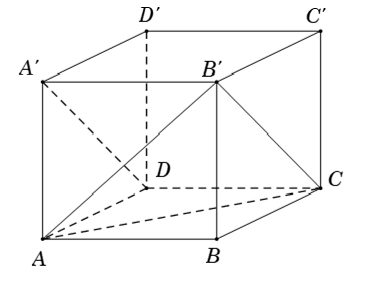
Ví dụ 4: Cho hình hộp ABCD.A’B’C’D’. Giả sử tam giác AB’C và A’DC’ đều có ba góc nhọn. Góc giữa hai tuyến đường thẳng AC và A’D là góc nào sau đây?

Hướng dẫn giải
Ta có : AC // A’C’ ( do AA’CC’ là hình bình hành) mà ∠DA'C' nhọn (do tam giác A’DC’ là tam giác nhọn) nên :
(AC, A'D) = (A'C', A'D) = ∠DA'C'
Chọn B
Ví dụ 5: Cho hình lập phương ABCD.A’B’C’D’. Chọn xác định sai?
A. Góc giữa AC và B’D’ bằng 90°
B. Góc giữa B’D’ và AA’ bằng 60°
C. Góc giữa AD và B’C bằng 45°
D. Góc giữa BD và A’C’ bằng 90°.
Hướng dẫn giải
Ta có (AA', B'D') = (BB', B'D') = ∠BB'C = 90°.
Khẳng định B sai. Chọn B.
Ví dụ 6: Cho tứ diện ABCD có BA = CD. Gọi I ; J ; E ; F lần lượt là trung điểm của AC ; BC ; BD ; AD. Góc (IE; JF) bằng
A. 30° B. 45° C. 60° D. 90°
Hướng dẫn giải
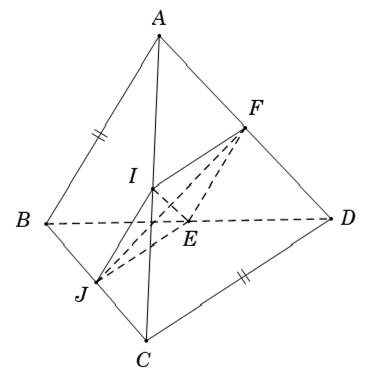
Ta có IF là đường trung bình của tam giác ACD
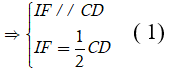
Lại có JE là đường trung bình của tam giác BCD
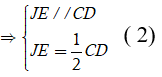
Từ (1) và (2) suy ra:

Do đó IJEF là hình thoi
Suy ra (IE; JF) = 90°.
Chọn D
Ví dụ 7: Cho tứ diện ABCD có AB = CD = a, IJ = (a√3)/2 (I; J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai tuyến đường thẳng AB và CD là
A. 30° B. 45° C. 60° D. 90°
Hướng dẫn giải
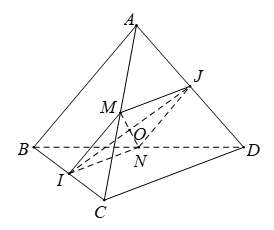
Chọn C
Gọi M; N lần lượt là trung điểm AC; BC.
Ta có:
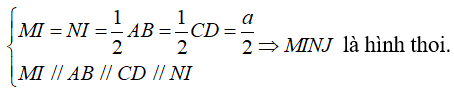
Gọi O là giao điểm của MN và IJ.
Ta có: ∠MIN = 2∠MIO .
Xét tam giác MIO vuông tại O, ta có:
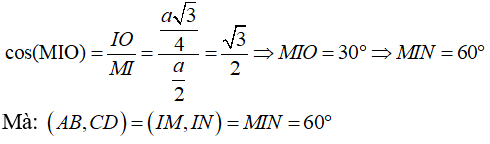
Ví dụ 8: Cho tứ diện ABCD có AB = AC = AD và
 . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→ ?
. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→ ?
A. 120° B. 90° C. 60° D.45°
Hướng dẫn giải
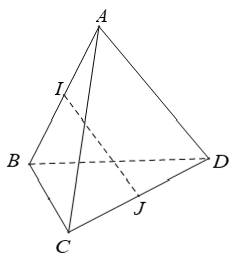
Chọn B
+ Xét tam giác ABC có AB = AC và ∠BAC = 60° nên tam giác ABC đều
Tương tự tam giác ABD đều.
⇒ BC = BD (= AB)
+ Xét tam giác ACD và tam giác BCD có :
BC = AC.
AD = BD
CD chung
⇒ Δ BCD = Δ ACD( c.c.c) ⇒ BJ = AJ
⇒ Tam giác AJB là tam giác cân tại J. Lại có, JI là đường trung tuyến nên đồng thời là đường cao.
⇒ IJ ⊥ AB.
⇒ góc giữa cặp vectơ AB→ và IJ→ là 90°
Câu 1: Cho tứ diện đều ABCD. Số đo góc giữa hai tuyến đường thẳng AB và CD bằng:
A. 60° B. 30° C. 90° D. 45°
Hiển thị lời giải

+ Gọi M là trung điểm của CD
+ Tam giác ACD và tam giác BCD là tam giác đều (vì ABCD là tứ diện đều) có AM; BM là hai tuyến đường trung tuyến ứng với cạnh CD nên đồng thời là đường cao.

Suy ra AB→ ⊥ CD→ nên số đo góc giữa hai tuyến đường thẳng AB và CD bằng 90°.
Chọn C
Câu 2: Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu?
A. 0° B. 30° C. 90° D. 60°
Hiển thị lời giải

Gọi M là trung điểm của CD
Vì ABCD là tứ diện đều nên những tam giác ACD và BCD là tam giác đều nên:

Suy ra AO→ ⊥ CD→ nên số đo góc giữa hai tuyến đường thẳng AO và CD bằng 90°.
Chọn C
Câu 3: Cho hình chóp S.ABC có SA = SB và CA = CB. Tính số đo của góc giữa hai tuyến đường thẳng chéo nhau SC và AB
A. 30° B. 45° C. 60° D. 90°
Hiển thị lời giải

Xét:

Vậy SC và AB vuông góc với nhau.
Chọn D
Câu 4: Cho hình chóp S.ABCD có tất cả những cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ; CD)bằng:
A . 90° B. 45° C. 30° D. 60°
Hiển thị lời giải

Chọn D
Gọi O là tâm của hình thoi ABCD.
+ Ta có: OJ là đường trung bình của tam giác BCD nên
OJ // CD
⇒ (IJ; CD) = (IJ, JO)
+ Xét tam giác IOJ có

⇒ tam giác IOJ đều.
Vậy góc giữa IJ và CD bằng góc giữa IJ và OJ
bằng góc ∠IJO = 60°
Chọn D.
Câu 5: Cho hình chóp S.ABCD có cạnh SA = x, tất cả những cạnh còn sót lại đều bằng a. Tính số đo của góc giữa hai tuyến đường thẳng SA và SC
A. 30° B. 45° C. 60° D.90°
Hiển thị lời giải

Theo giả thiết, ta có: AB = BC = CD = DA = a nên ABCD là hình thoi cạnh a.
Gọi O là giao điểm của AC và BD. Ta có ΔCBD = ΔSBD (c-c-c) .
Suy ra hai tuyến đường trung tuyến tương ứng CO và SO bằng nhau.
Xét tam giác SAC, ta có SO = CO = (1/2)AC .
Do đó tam giác SAC vuông tại S (tam giác có đường trung tuyến bằng nửa cạnh đáy). Vậy SA ⊥ SC
Chọn D.
Câu 6: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos( AB; DM) bằng
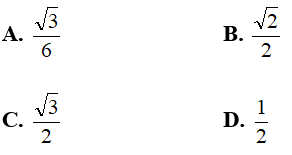 Hiển thị lời giải
Hiển thị lời giải

Chọn A
Không mất tính tổng quát, giả sử tứ diện ABCD có cạnh bằng a.
Gọi H là tâm đường tròn ngoại tiếp ΔBCD ⇒ AH ⊥ (BCD)
Gọi E là trung điểm AC ⇒ ME // AB ⇒ (AB, DM) = (ME, MD)
Ta có:

Do những mặt của tứ diện đều là tam giác đều, từ đó ta thuận tiện và đơn giản tính được độ dài những cạnh của tam giác MED : ME = a, ED = MD = (√3/2)a
Xét tam giác MED, ta có:

Câu 7: Cho hình chóp S.ABCD có đáy là hình vuông vắn ABCD cạnh bằng a và những cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN; SC) bằng
A. 30° B. 45° C. 60° D.90°
Hiển thị lời giải
Chọn D
Gọi O là tâm của hình vuông vắn ABCD nên O là tâm đường tròn ngoại tiếp của hình vuông vắn ABCD (1)

Ta có: SA = SB = SC = SD nên S nằm trên trục của đường tròn ngoại tiếp hình vuông vắn ABCD (2)
Từ (1) và (2) ⇒ SO ⊥ (ABCD)
Từ giả thiết ta có: MN // SA (do MN là đường trung bình của tam giác SAD).
⇒ (MN; SC) = (SA; SC).
Xét tam giác SAC, ta có:
 ⇒ ΔSAC vuông tại S ⇒ SA ⊥ SC
⇒ ΔSAC vuông tại S ⇒ SA ⊥ SC
⇒ (SA, SC) = (MN, SC) = 90°
Câu 8: Cho tứ diện ABCD có AB = AC = AD và ∠BAC = ∠BAD = 60°, ∠CAD = 90°. Gọi I và J lần lượt là trung điểm của AB và CD Hãy xác định góc giữa cặp vectơ IJ→ và CD→ ?
A. 45° B. 90° C. 60° D. 120°
Hiển thị lời giải
Chọn B
Ta có BAC và BAD là 2 tam giác đều, I là trung điểm của AB nên CI = DI
(2 đường trung tuyến của 2 tam giác đều chung cạnh AB)
⇒ Tam giác CID là tam giác cân ở I.
Mà IJ là đường trung tuyến nên đồng thời là đường cao nên IJ ⊥ CD
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
 Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!
Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!






Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.


Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù phù hợp với nội quy phản hồi trang web sẽ bị cấm phản hồi vĩnh viễn.
[embed]https://www.youtube.com/watch?v=MID2a_9GYYI[/embed]