Thủ Thuật về Giá trị lớn số 1 của hàm số y 3 2 cos x 2 pi chia 3 2022
Họ và tên học viên đang tìm kiếm từ khóa Giá trị lớn số 1 của hàm số y 3 2 cos x 2 pi chia 3 được Update vào lúc : 2022-04-18 04:40:09 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Gọi M m, lần lượt là giá trị lớn số 1 và nhỏ nhất của hàm số (y = 3 + 2cos ^2left( x + dfracpi 3 right)). Khi đó (m^2 + M^2) bằng:
Hãy luôn nhớ cảm ơn và vote 5*
nếu câu vấn đáp hữu ích nhé!


XEM GIẢI BÀI TẬP SGK TOÁN 11 - TẠI ĐÂY
Hàm số (y = sin x) có tập xác định là:
Tập giá trị của hàm số (y = sin x) là:
Hàm số (y = cos x) nghịch biến trên mỗi khoảng chừng:
Đồ thị hàm số (y = tan x) luôn đi qua điểm nào dưới đây?
Hàm số nào sau đây không là hàm số lẻ?
Hàm số nào sau đây có đồ thị không là đường hình sin?
Đường cong trong hình hoàn toàn có thể là đồ thị của hàm số nào dưới đây?
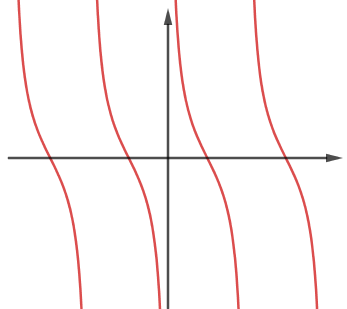
Hàm số (y = dfrac1 - sin 2xcos 3x - 1) xác định trên:
Tìm chu kì của hàm số (y = fleft( x right) = tan 2x).
Tìm chu kì của những hàm số sau (fleft( x right) = sin 2x + sin x)
Tìm chu kì của những hàm số sau (y = tan x.tan 3x).
Tìm chu kì của những hàm số sau (y = sin sqrt x )
Khẳng định nào sau đây là đúng?
Hàm số nào sau đây không chẵn, không lẻ?
Hàm số nào trong những hàm số sau có đồ thị nhận (Oy) làm trục đối xứng ?
Giá trị nhỏ nhất của hàm số (y = 2cos ^2x + sin 2x) là
Cho hàm số lượng giác (f(x) = tan x - dfrac1sin x).
Tập xác định của hàm số (y = dfrac12cos x - 1) là:
Tập xác định của hàm số (y = dfraccot xsin x - 1) là:
Tập xác định của hàm số (y = sqrt 1 - cos 2017x ) là
Hàm số nào sau đây là hàm số chẵn?
Hình nào dưới đây màn biểu diễn đồ thị hàm số (y = f(x) = 2sin 2x?)
Hình nào sau đây là đồ thị hàm số (y = left| sin x right|?)
Giải phương trình (cot left( 3x - 1 right) = - sqrt 3 .)
Giải phương trình $sin xcos x + 2left( sin x + cos x right) = 2$.
Trong những phương trình sau phương trình nào có nghiệm ?
 Tải app VietJack. Xem lời giải nhanh hơn!
Tải app VietJack. Xem lời giải nhanh hơn! Quảng cáo
Để tìm được giá trị lớn số 1;giá trị nhỏ nhất của hàm số ta cần để ý quan tâm:
+ Với mọi x ta luôn có: - 1 ≤ cosx ≤ 1; -1 ≤ sinx ≤ 1
+Với mọi x ta có: 0 ≤ |cosx| ≤ 1 ;0 ≤ |sinx| ≤ 1
+ Bất đẳng thức bunhia –copski: Cho hai bộ số (a1; a2) và (b1;b2) khi đó ta có:
(a1.b1+ a2.b2 )2 ≤ ( a12+ a22 ).( b12+ b22 )
Dấu “=” xảy ra khi: a1/a2 = b1/b2
+ Giả sử hàm số y= f(x) có mức giá trị lớn số 1 là M và giá trị nhỏ nhất là m. Khi đó; tập giá trị của hàm số là [m; M].
+ Phương trình : a. sinx+ b. cosx= c có nghiệm khi và chỉ khi a2 + b2 ≥ c2
Ví dụ 1. Tìm giá trị lớn số 1 M và giá trị nhỏ nhất m của hàm số y= 1- 2|cos3x|.
A. M=3 ; m= - 1.
B. M= 1 ; m= -1.
C. M=2 ;m= -2.
D. M=0 ; m= -2.
Lời giải:.
Chọn B.
Với mọi x ta có : - 1 ≤ cos3x ≤ 1 nên 0 ≤ |cos3x| ≤ 1
⇒ 0 ≥ -2|cos3x| ≥ -2

Ví dụ 2: Hàm số y= 1+ 2cos2x đạt giá trị nhỏ nhất tại x= x0. Mệnh đề nào sau đây là đúng?
A.x0=π+k2π, kϵZ .
B.x0=π/2+kπ, kϵZ .
C.x0=k2π, kϵZ .
D.x0=kπ ,kϵZ .
Lời giải:.
Chọn B.
Ta có - 1 ≤ cosx ≤ 1 ⇒ - 0 ≤ cos2x ≤ 1 ⇒ 1 ≤ 1+2cos2x ≤ 3
Do đó giá trị nhỏ nhất của hàm số bằng 1 .
Dấu ‘=’ xảy ra khi cosx=0 ⇒ x=π/2+kπ, kϵZ .
Quảng cáo
Ví dụ 3: Tìm giá trị lớn số 1 M và giá trị nhỏ nhất m của hàm số y= sin2x+ 2cos2x.
A.M= 3 ;m= 0
B. M=2 ; m=0.
C. M=2 ; m= 1.
D.M= 3 ; m= 1.
Lời giải:.
Chọn C.
Ta có: y = sin2 x+ 2cos2x = (sin2x+ cos2x) + cos2x = 1+ cos2 x.
Do: -1 ≤ cosx ≤ 1 nên 0 ≤ cos2 x ≤ 1 ⇒ 1 ≤ cos2 x+1 ≤ 2
Suy ra giá trị lớn số 1 của hàm số là M= 2 và giá trị nhỏ nhất của hàm số là m= 1
Ví dụ 4: Tìm giá trị lớn số 1 M và giá trị nhỏ nhất m của hàm số y= 4sinx - 3
A.M= 1; m= - 7
B. M= 7; m= - 1
C. M= 3; m= - 4
D. M=4; m= -3
Lời giải
Chọn A
Ta có : - 1 ≤ sinx ≤ 1 nên - 4 ≤ 4sinx ≤ 4
Suy ra : - 7 ≤ 4sinx-3 ≤ 1
Do đó : M= 1 và m= - 7
Ví dụ 5: Tìm tập giá trị T của hàm số y= -2cos2x + 10 .
A. [5; 9]
B.[6;10]
C. [ 8;12]
D. [10; 14]
Lời giải:
Chọn C
Với mọi x ta có : - 1 ≤ cos2x ≤ 1 nên-2 ≤ -2cos2x ≤ 2
⇒ 8 ≤ -2cos2x+10 ≤ 12
Do đó tập giá trị của hàm số đã cho là : T= [ 8 ;12]
Quảng cáo
Ví dụ 6: Tính độ dài giá trị của hàm số y= 10- 2cos2x
A. 10
B. 8
C.6
D. 4
Lời giai
Với mọi x ta có: - 1 ≤ cos2x ≤ 1 nên-2 ≤ -2cos2x ≤ 2
Suy ra: 8 ≤ 10-2cos2x ≤ 12
Do đó; tập giá trị của hàm số đã cho là: [8; 12] và độ dài đoạn giá trị của hàm số là : 12 – 8= 4
Chọn D.
Ví dụ 7: Tính tổng giá trị nhỏ nhất m và giá trị lớn số 1 M của hàm số sau: y= √3 sin( 2016x+2022)
A. - 4032
B. √3
C. -√3
D. 0
Lời giải:
Chọn D
Với mọi x ta có :- 1 ≤ sin(2016x+2022) ≤ 1
⇒ -√3 ≤ √3sin(2016x+2022) ≤ √3
Do đó giá trị nhỏ nhất của hàm số là -√3 và giá trị lớn số 1 của hàm số là √3
⇒ Tổng giá trị lớn số 1 và nhỏ nhất của hàm số là - √3+ √3=0
Ví dụ 8: Tìm giá trị nhỏ nhất m của hàm số y= 1/(1+sinx)
A. m= 1/2
B. m= 1/√2
C. m= 1
D. m= √2
Lời giải:
Chọn A
Điều kiện xác định : sinx ≠ -1 hay x ≠ (- π)/2+k2π
+ Với mọi x thỏa mãn điều kiện ta có : - 1
+ Nếu mẫu 1+ sinx > 0 thì hàm số đạt giá trị nhỏ nhất lúc và chỉ khi một+ sinx đạt giá trị lớn số 1
Hay 1+ sinx=2 < ⇒ sinx= 1( thỏa mãn điều kiện) .
Khi đó ymin = 1/2
Vậy hàm số đạt giá trị nhỏ nhất là một trong/2 khi sinx= 1
Ví dụ 9: Tìm giá trị lớn số 1 M, giá trị nhỏ nhất m của hàm số: y= 2018sin( 9x+π/100)+2000
A. m=18 ; M=4018
B. m = -18; M= 18
C. m=-18; M= 4018
D. Đáp án khác
Lời giải:
Chọn C
Hàm số xác định trên R.
Với mọi x ta có: - 1 ≤ sin( 9x+π/100) ≤ 1 nên - 2022 ≤ 2018sin( 9x+π/100) ≤ 2022
⇒ -18 ≤ 2018sin( 9x+π/100)+2000 ≤ 4018
⇒ giá trị nhỏ nhất của hàm số là -18 khi sin( 9x+π/100)=-1
Giá trị lớn số 1 của hàm số là 4018 khi sin( 9x+π/100)=1
Ví dụ 10: Tìm giá trị lớn số 1 M và giá trị nhỏ nhất m của hàm số y= ∜sinx- √cosx.
A. m= -1; M=1.
B. m = 0; M=1
C. m= -1;M=0
D. m= -1 và M không tồn tại.
Lời giải:
Chọn A
Với mọi x thỏa mãn điều kiện : sinx > 0 và cosx > 0 .Ta có:

Vậy hàm số đạt giá trị nhỏ nhất là m= – 1 khi: (sinx=0 và cosx=1 ⇒ x= k2π.
Hàm số đạt giá trị lớn số 1 là M=1 khi (sinx=1 và cosx=0 ⇒ x= π/2+k2π.
Ví dụ 11. Gọi M và m lần lượt là giá trị lớn số 1 và giá trị nhỏ nhất của hàm số : y= cos2 x – 6cosx + 11. Tính M.m
A.30
B.36
C.27
D.24
Lời giải:
Ta có: cos2 x – 6cosx +11 = ( cos2x – 6cosx + 9) +2 = (cosx -3)2 + 2
Do - 1 ≤ cosx ≤ 1 ⇒ - 4 ≤ cosx-3 ≤ -2
⇒ 0 ≤ (cosx-3)^2 ≤ 16
⇒ 2 ≤ (cosx-3)^2+2 ≤ 18
Suy ra:M= 18 và m= 2 nên M. m= 36.
Chọn B.
Ví dụ 12. Gọi M và lần lượt là giá trị lớn số 1; giá trị nhỏ nhất của hàm số
y=(cosx+2sinx+3)/(2cosx-sinx+4). Tính S= M+11m
A.4
B.5
C. 6
D. 8
Lời giải:.
Gọi y0 là một giá trị của hàm số.
Khi đó phương trình y0=(cosx+2sinx+3)/(2cosx-sinx+4) có nghiệm.
⇒ y0.( 2cosx- sinx + 4) = cosx +2sinx + 3 có nghiệm
⇒ 2y0.cosx – sinx.y0 + 4y0- cosx – 2sinx – 3=0 có nghiệm
⇒ ( 2y0 -1)cosx – ( y0+2).sinx =3- 4y0 (*)
Phương trình (*) có nghiệm khi và chỉ khi :
(2y0-1)2 + ( y0 + 2)2 ≥ (3-4y0)2
⇒ 4y02 – 4y0 +1 +y02 +4y0 + 4 ≥ 9-24y0+16y02
⇒ 11y02 – 24y0 + 4 ≤ 0 2/11 ≤ y0 ≤ 2
Suy ra: M=2 và m=2/11 nên S= M+ 11m= 4
Chọn A.
Ví dụ 13. Cho hàm số y= √(1+2sin2 x)+ √(1+2〖cos2 x)-1. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn số 1 của hàm số. Khi đó; giá trị M+ m gần với giá trị nào nhất?
A. 3,23
B. 3,56
C. 2,78
D.2,13
Lời giải:
+ Xét t= √(1+2sin2 x)+ √(1+2cos2 x)
⇒ t2 = 1+ 2sin2 x+ 1+ 2cos2 x+ 2. √((1+2sin2 x).( 1+2cos2 x) )
=4+2√(3+ sin2 2x)
Mà sin22x ≥ 0 nên t2 ≥ 4+ 2√3
Mà t > 0 nên t ≥ √(4+2√3) =1+ √3
Suy ra: y= t-1 ≥ √3
Dấu “=” xảy ra khi sin2x=0 .
+ Lại có:
√(1+2sin2 x)+ √(1+2cos2 x) ≤ √((1^2+ 1^2 ).( 1+2sin2x+ 1+2cos2 x) )= 2√2
⇒ y= √(1+2sin2 x)+ √(1+2cos2 x)-1 ≤ 2√2-1
Dấu “=” xảy ra khi sin2 x= cos2x
Vậy {(m= √3 và M=2√2-1) ⇒ M+ m≈3,56
Chọn B.
Câu 1:Gọi M; m lần lượt là giá trị lớn số 1 và giá trị nhỏ nhất của hàm số y=8sin2x+3cos2x . Tính P= M- 2m.
A. P= - 1
B. P= 1
C. P= 2
D. P=0
Hiển thị lời giải
Chọn A.
Ta có: y = 8sin2 x + 3cos2x = 8sin2x + 3( 1 – 2sin2x ) = 2sin2x+ 3.
Mà -1 ≤ sinx ≤ 1 ⇒ 0 ≤ sinx ≤ 1 ⇒ 3 ≤ 2sinx+3 ≤ 5 ⇒ 3 ≤ y ≤ 5.
Suy ra: M= 5 và m= 3
Do đó: P = 5- 2.3= - 1
Câu 2:Tìm giá trị lớn số 1 M của hàm số y= 4sin2x + 3.cos2x .
A. M= 3
B. M= 1
C. M= 5
D. M= 4
Hiển thị lời giải
Chọn C.
Ta có: y = 4sin2x+ 3cos2x = 5.( 4/5.sin2x+ 3/5 cos2x).
Đặt cosα= 4/5 và sinα= 3/5
Khi đó: y= 5( cosα.sin2x+sinα.cos2x)=5.sin( α+2x)
⇒ - 5 ≤ y ≤ 5
Suy ra M= 5.
Câu 3:Gọi M ; m lần lượt là giá trị lớn số 1 và giá trị nhỏ nhất của hàm số y= sin2x – 4sinx+ 5. Tính M+ m.
A.3
B.8
C.10
D.12
Hiển thị lời giải
Chọn D.
Ta có: y= sin2x – 4sinx+ 5= ( sinx- 2)2 + 1.
Do: -1 ≤ sinx ≤ 1 nên-3 ≤ sinx-2 ≤ -1
⇒ 1 ≤ ( sinx-2)2 ≤ 9 ⇒ 2 ≤ ( sinx-2)2+1 ≤ 10 .
Suy ra: M=10 và m = 2
Do đó; M+ m = 12
Câu 4:Cho hàm số y= cos2x- cosx có tập giá trị là T. Hỏi có tất cả bao nhiêu giá trị nguyên thuộc T.
A. 1
B. 2
C. 3
D. 4
Hiển thị lời giải
Chọn C.
Ta có: cos2x- cosx = (cosx- 1/2)2- 1/4 .
Do - 1 ≤ cosx ≤ 1 nên (- 3)/2 ≤ cosx- 1/2 ≤ 1/2
⇒ 0 ≤ ( cosx- 1/2)2 ≤ 9/4 ⇒ (- 1)/4 ≤ ( cosx- 1/2)2- 1/4 ≤ 2.
Do đó (- 1)/4 ≤ y ≤ 2. Vậy tập giá trị của hàm số là [(- 1)/4;2]
⇒ Trong đoạn [ -1/4;2] có ba giá trị nguyên thỏa mãn là 0; 1 và 2.
Do đó có 3 giá trị thỏa mãn.
Câu 5:Hàm số y= cos2x+ 2sinx+ 2 đạt giá trị nhỏ nhất tại x0. Mệnh đề nào sau đây là đúng.
A. x= (-π)/2+k2π.
B. x= π/2+k2π.
C. x= k π
D. x= k2π
Hiển thị lời giải
Chọn B.
Ta có: cos2x+ 2sinx+ 2 = 1- sin2x+ 2sinx + 2= - sin2x + 2sinx+ 3 = - (sinx-1)2 + 4
Mà - 1 ≤ sinx ≤ 1 nên-2 ≤ sinx-1 ≤ 0
Suy ra: 0 ≤ ( sinx-1)2 ≤ 4 ⇒ -4 ≤ - (sinx-1)2 ≤ 0
⇒ 0 ≤ 4 - (sinx-1)2 ≤ 4
Suy ra giá trị nhỏ nhất của hàm số bằng 0.
Dấu “=” xảy ra khi và chỉ khi sinx= 1 ⇒ x= π/2+k2π.
Câu 6:Tìm giá trị lớn số 1 M và nhỏ nhất m của hàm số y= sin4x -2 cos2x+ 1.
A.M= 2; m= - 2
B.M=1; m=0
C.M=4;m= - 1
D M=2;m= - 1
Hiển thị lời giải
Chọn D.
Ta có: sin4x- 2cos2x + 1= sin4x – 2( 1- sin2x) + 1
= sin4x + 2sin2x - 1 = ( sin2 x +1)22 - 2
Mà: 0 ≤ sin2 x ≤ 1 nên 1 ≤ sin2 x+1 ≤ 2
Suy ra: 1 ≤ ( sin2 x+1)2 ≤ 4 ⇒ -1 ≤ ( sin2 x+1)2-2 ≤ 2 .
Nên M= 2; m= - 1
Câu 7:Tìm giá trị nhỏ nhất của hàm số y= 4sin4x – cos4x.
A. - 3
B. - 1
C. 3
D. 5
Hiển thị lời giải
Chọn B.
Ta có: y= 4sin4x – cos4x= 4.((1-cos2x)/2)2-(2cos2 2x-1)
= 1- 2cos2x+ cos22x – 2cos2x + 1
= - cos42x - 2cos2x + 2 = - (cos2x+ 1)2 + 3
Mà -1 ≤ cos2x ≤ 1 ⇒ 0 ≤ cos2x+1 ≤ 2 ⇒ 0 ≤ (cos2x+1)2 ≤ 4 ⇒ -1 ≤ -(cos2x+1)2+3 ≤ 3
Suy ra m= - 1.
Câu 8:Gọi M và m lần lượt là giá trị lớn số 1 và giá trị nhỏ nhất của hàm số y= 2( sinx - cosx). Tính P= M+ 2m.
A. 2
B. - 2√2
C. - √2
D. 4√2
Hiển thị lời giải
Chọn B
Ta có : 2( sinx- cosx)=2√2 sin( x- π/4)
Với mọi x thì : - 1 ≤ sin( x- π/4) ≤ 1
⇒ - 2√2 ≤ 2√2.sin( x- π/4) ≤ 2√2
Vậy giá trị lớn số 1 và giá trị nhỏ nhất của hàm số đã cho là M= 2√2 và m= -2√2
⇒ P= M+ 2m= - 2√2
Câu 9:Giá trị lớn số 1 và giá trị nhỏ nhất của hàm số y= √(1- cos2 x)+1là:
A. 2 và 1
B. 0 và 3
C. 1 và 3
D.1 và 1+ √2
Hiển thị lời giải
Ta có : √(1- cos2 x)= √(sin2 x)= |sinx|
Do đó; hàm số y= √(1- cos2 x)+1=|sinx|+1
Với mọi x ta có: - 1 ≤ sinx ≤ 1 nên 0 ≤ |sinx| ≤ 1
⇒ 1 ≤ |sinx|+1 ≤ 2
⇒ giá trị lớn số 1 và giá trị nhỏ nhất của hàm số đã cho là 2 và 1.
Chọn A
Câu 10:Giá trị nhỏ nhất của hàm số y= 4sin2 x+ 6cos2x+ 2 là
A. 4
B. 6
C. 8
D. 10
Hiển thị lời giải
Ta có: 4sin2x + 6cos2 x+ 1= 2( 1- cos2x) + 3( 1+cos2x) + 2 = cos2x+ 7
Với mọi x ta luôn có: - 1 ≤ cos2x ≤ 1 nên 6 ≤ cos2x+7 ≤ 8
Suy ra: giá trị nhỏ nhất của hàm số là 6
Chọn B.
Câu 11:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số sau
A.max y=4,min y=3/4
B.max y=3,min y=2
C.max y=4,min y=2
D.max y=3,min y=3/4
Hiển thị lời giải
Đặt t=sin2x, 0 ≤ t ≤ 1 ⇒ cos2x=1-2t
⇒ y= 2t+(1-2t)2=42-2t+1=(2t-1/2)2+3/4
Do 0 ≤ t ≤ 1 ⇒ -1/2 ≤ 2t-1/2 ≤ 3/2 ⇒ 0 ≤ (2t-1/2)2 ≤ 9/4 ⇒ 3/4 ≤ y ≤ 3 .
Vậy max y=3 đạt được khi x=π/2+kπ .
min y=3/4 đạt được khi sin2x=1/4 .
Chọn D.Câu 12:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số sau y = 3sinx + 4cosx + 1
A. max y=6,min y=-2
B. max y=4,min y=-44
C. max y=6,min y=-4
D.max y=6,min y=-1
Hiển thị lời giải
Áp dụng bất đẳng thức bunhia- xcopski: (ac+bd)2 ≤ (c2+d2)(a2+b2) .
Đẳng thức xảy ra khi a/c=b/d .
Ta có: (3sinx+4cosx)2 ≤ (32+42)(sin2+cos2)=25
⇒ 5 ≤ 3sinx+4cosx ≤ 5 ⇒ -4 ≤ y ≤ 6
Vậy max y=6 , đạt được khi tanx=3/4 .
min y=-4 , đạt được khi tanx=-3/4.
Chọn C.
Câu 13:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số sau y=2sin2x+3sin2x-4cos2x
A. min y= -3√2 -1, max y=3√2 +1
B. min y= -3√2 -1, max y=3√2 -1
C. min y= -3√2 , max y=3√2 -1
D. min y= -3√2 -2, max y=3√2 -1
Hiển thị lời giải
Ta có: y= 2sin2 x + 3sin2x - 4cos2x
= 1 – cos2x + 3sin2x - 2( 1+ cos2x)
=3sin2x-3cos2x-1=3√2sin(2x-π/4)-1
Mà -1 ≤ sin(2x- π/4) ≤ 1 ⇒ - 3√2 ≤ 3√2sin(2x- π/4) ≤ 3√2
⇒ - 3√2-1 ≤ 3√2sin( 2x- π/4)-1 ≤ 3√2-1
Suy ra min y= -3√2 -1, max y=3√2 -1 .
Chọn B.
Câu 14:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số y=sin2x+3sin2x+3cos2x
A. min y= 2+√10 , max y=2-√10
B. min y= 2+√5, max y=2+√5
C. min y= 2+√2, max y=2-√2
D. min y= 2+√7, max y=2-√7
Hiển thị lời giải
Ta có:
Áp dụng bất đẳng thức bunhia- xcopki ta có :
- √(32+ 12 ) ≤ 3sin2x+cos2x ≤ √(32+ 12 )
Suy ra : -√10 ≤ 3sin2x+cos2x ≤ √10
⇒ 2-√10 ≤ y ≤ 2+√10
Từ đó ta đã có được: maxy=2+√10;miny=2-√10.
Chọn A.
Câu 15:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số sau y=sinx+ √(2-sin2)
A.min y= 0, max y=3
B.min y= 0, max y=4
C.min y= 0, max y=6
D.min y= 0, max y=2
Hiển thị lời giải
Ta có 0 ≤ y ∀x và y2=2+2sin√(2-sin2)
Mà 2|sin√(2-sin2)| ≤ sin2+2-sin2=2
Suy ra 0 ≤ y2 ≤ 4 ⇒ 0 ≤ y ≤ 4
min y=0 đạt được khi x=-π/2+k2π
max y=2 đạt được khi x=π/2+k2π
Chọn D.
Câu 16:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số sau y=(sin2x+2cos2x+3)/(2sin2x-cos2x+4)
A. min y= -2/11, max y=2
B. min y= 2/11, max y=3
C. min y= 2/11, max y=4
D. min y= 2/11, max y=2
Hiển thị lời giải
+ Áp dụng bất đẳng thức bunhia-xcopski ta có:
(2sin2x – cos2x)2 ≤ (22+(-1)2). ( sin22x + cos22x) = 5
⇒ -√5 ≤ 2sin2x-cos2x ≤ √5
⇒ 4-√5 ≤ 4+ 2sin2x-cos2x ≤ 4+√5
⇒ 4+ 2sin2x- cos2x > 0 với mọi x.
+ Ta có:
y=(sin2x+2cos2x+3)/(2sin2x-cos2x+4)
⇒ y. 2sin2x – y.cos2x + 4y = sin2x +2cos2x + 3
⇔ (2y-1)sin2x-(y+2)cos2x=3-4y (*)
Phương trình (*) có nghiệm khi và chỉ khi:
⇒ (2y-1)2+(y+2)2 ≥ (3-4y)2
⇔ 11y2-24y+4 ≤ 0 ⇔ 2/11 ≤ y ≤ 2
Suy ra: min y= 2/11, max y=2 .
Chọn D.
Câu 17:Tìm tập giá trị lớn số 1, giá trị nhỏ nhất của hàm số y=(2sin23x+4sin3xcos3x+1)/(sin6x+4cos6x+10)
A. min y= (11-9√7)/83, max y=(11+9√7)/83
B. min y= (22-9√7)/11, max y=(22+9√7)/11
C. min y= (33-9√7)/83, max y=(33+9√7)/83
D. min y= (22-9√7)/83, max y=(22+9√7)/83
Hiển thị lời giải
+Áp dụng bất đẳng thức bunhia- xcopski ta có:
( sin6x+4cos6x)2 ≤ (12+42). ( sin26x+ cos26x)= 17
⇒ -√17 ≤ sin6x+4cos6x ≤ √17
⇒ sin6x+4cos6x+10 ≥ 10-√17 > 0 ∀x thuộc R
Do đó; hàm số xác định với mọi x.
+ ta có: y=(2sin6x-cos6x+2)/(sin6x+4cos6x+10)
⇒ (y-2)sin6x+(4y+1)cos6x=2-10y
Phương trình trên có nghiệm khi và chỉ khi:
⇒ (y-2)2+(4y+1)2 ≥ (2-10y)2 ⇔ 83y2-44y-1 ≤ 0
⇒ (22-9√7)/83 ≤ y ≤ (22+9√7)/83.
Suy ra: min y= (22-9√7)/83, max y=(22+9√7)/83
Chọn D.
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
 Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!
Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!






Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.


Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù phù hợp với nội quy phản hồi trang web sẽ bị cấm phản hồi vĩnh viễn.
[embed]https://www.youtube.com/watch?v=x0zG5GLyEi8[/embed]