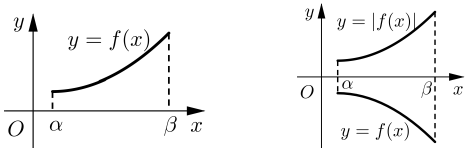Kinh Nghiệm về Tìm tất cả những giá trị thực của tham số m để hàm số y bằng Mới Nhất
Hoàng Nhật Mai đang tìm kiếm từ khóa Tìm tất cả những giá trị thực của tham số m để hàm số y bằng được Cập Nhật vào lúc : 2022-04-02 16:07:07 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Nội dung chính
- Tóm tắt lý thuyết tính đồng biến nghịch biến1. Định nghĩa đồng biến, nghịch biến2. Định lí3. Định lí mở rộng4. Qui tắc xét tính đơn điệu của hàm sốPhân dạng bài tập tìm m để hàm số đồng biến, nghịch biến trên khoảngDạng 1. Tìm m để hàm số bậc 3 đơn điệu trên khoảngDạng 2. Biện luận đơn điệu của hàm phân thứcDạng 3: Tìm m để hàm số khác đơn điệu trên khoảngDạng 4: Tìm m để hàm số đồng biến nghịch biến trên RDạng 5: Tìm m để hàm số cho bởi đồ thị hàm F(x) đơn điệuDạng 6: Tìm m để hàm giá trị tuyệt đối đơn điệu trên khoảng chừng cho trướcLoại 2: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số dạng phân thức hữu tỉ đồng biến, nghịch biến trên tập D cho trước.Loại 3: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số chứa căn đồng biến, nghịch biến trên tập D cho trước.Loại 4: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số lượng giác đồng biến, nghịch biến trên tập D cho trước.Loại 5: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số mũ đồng biến, nghịch biến trên tập D cho trước.Loại 6: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số logarit đồng biến, nghịch biến trên tập D cho trước.Tài liệu tìm m để hàm số đồng biến, nghịch biến trên khoảngVideo liên quan
- lý thuyết trắc nghiệm hỏi đáp bài tập sgk
Tìm tất cả những giá trị thực của tham số m để hàm số y=-x2 +(m-1)x+2 nghịch biến trên khoảng chừng (1;2)
Các thắc mắc tương tự
Tìm m để hàm số đồng biến, nghịch biến trên khoảng chừng là một dạng toán tham số khi tham gia học về tính đồng biến, nghịch biến. Ở những cấp học nhỏ hơn, dạng toán này tồn tại dưới hình thức là một bài toán khó. Tuy nhiên, đến với chương trình toán THPT thì dạng toán này trở nên phổ biến, đặc biệt là chương trình toán 12. Đó là nguyên do Verbalearn sẽ giúp bạn thống kê lại toàn bộ kiến thức và kỹ năng ngay trong nội dung bài viết này.
Tóm tắt lý thuyết tính đồng biến nghịch biến
1. Định nghĩa đồng biến, nghịch biến
Cho hàm số y = f(x) xác định trên K , trong đó K là một khoảng chừng, đoạn hoặc nữa khoảng chừng.
a) Hàm số y = f(x) đồng biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).
b) Hàm số y = f(x) nghịch biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).
2. Định lí
Cho hàm số y = f(x) có đạo hàm trên K .
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K .
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K .
c) Nếu f’(x) = 0 với mọi x thuộc K thì hàm số f(x) không đổi trên K .
Chú ý: Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) > 0 trên khoảng chừng (a;b) thì hàm số f đồng biến trên đoạn [a;b]. Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) < 0 trên khoảng chừng (a;b) thì hàm số f nghịch biến trên đoạn [a;b].
3. Định lí mở rộng
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) ≥ 0 với mọi x thuộc K và f’(x) = 0 xảy ra tại một số trong những hữu hạn điểm của K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) ≤ 0 với mọi x thuộc K và f’(x) = 0 xảy ra tại một số trong những hữu hạn điểm của K thì hàm số f(x) nghịch biến trên K.
4. Qui tắc xét tính đơn điệu của hàm số
Bước 1: Tìm tập xác định.
Bước 2: Tính đạo hàm f’(x). Tìm những điểm xᵢ (i = 1, 2, …,n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
Bước 3: Sắp xếp những điểm xᵢ theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Nêu kết luận về những khoảng chừng đồng biến, nghịch biến của hàm số.
Phân dạng bài tập tìm m để hàm số đồng biến, nghịch biến trên khoảng chừng
Chúng ta sẽ tìm hiểu 6 dạng như sau để có cái nhìn tổng quan nhất về những bài tập biện luận tham số m liên quan đến tính đồng biến và nghịch biến trên khoảng chừng của hàm số.
Dạng 1. Tìm m để hàm số bậc 3 đơn điệu trên khoảng chừng
Phương pháp giải:
Hàm số đồng biến trên ℝ thì y’ ≥ 0, ∀ x ∊ ℝ ⇔ hoặc suy biến
Hàm số nghịch biến trên ℝ thì y’ ≤ 0, ∀ x ∊ ℝ ⇔ hoặc suy biến
A.
B.
C.
D.
Lời giải
Chọn A
Tập xác định D = ℝ, yêu cầu của bài toán đưa đến giải bất phương trình
mx2 + 14mx + 14 ≤ 0, ∀ x ≥ 1 tương đương với
Dễ dàng đã có được g(x) là hàm tăng ∀ x ∊ [1; +∞), suy ra
Kết luận:
A. m ≥ 0
B.
C. m ≤ 0
D.
Lời giải
Chọn D
y’ = mx2 – 6mx = 0
Hàm số y = x3 – 3mx2 – m nghịch biến trên khoảng chừng (0;1) ⇔ 2m ≥ 1 ⇔ m ≥ ½
Ví dụ 3: Tìm tất cả những giá trị của tham số m để hàm số y = x3 + 3x2 – mx + 1 đồng biến trên khoảng chừng (-∞;0).A. m ≤ 0
B. m ≥ -2 .
C. m ≤ -3
D. m ≤ -1
Lời giải
Chọn C
Tập xác định: D = ℝ
Đạo hàm: y’ = 3x2 + 6x – m
Hàm số đồng biến trên khoảng chừng (-∞;0) khi và chỉ khi y’ ≥ 0, ∀ x < 0
⇔ 3x2 + 6x – m ≥ 0, ∀ x < 0
Cách 1:
3x2 + 6x – m ≥ 0, ∀ x < 0 ⇔ 3x2 + 6x ≥ m, ∀ x < 0.
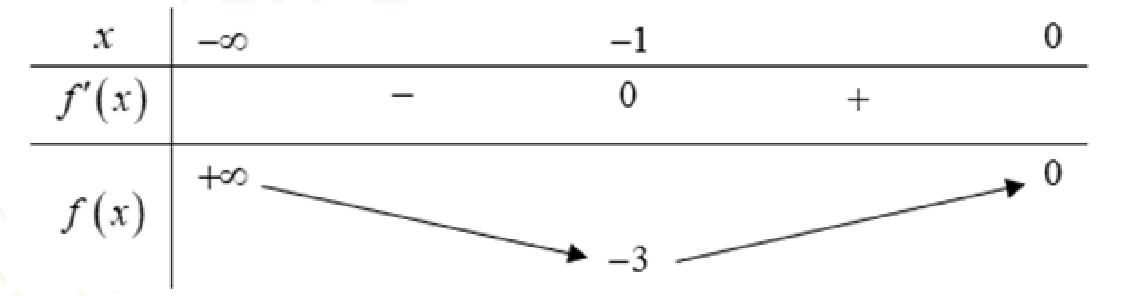
Xét hàm số f(x) = 3x2 + 6x trên khoảng chừng (-∞;0), ta có:
f’(x) = 6x + 6. Xét f’(x) = 0 ⇔ 6x + 6 = 0 ⇔ x = -1. Ta có f(-1) = -3.
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có: m ≤ -3 .
Cách 2:
Ta có ∆’ = 9 + 3m
Nếu ∆’ ≤ 0 ⇔ m ≤ -3 thì y’ ≥ 0, ∀ x ∊ ℝ ⇒ y’ ≥ 0, ∀ x < 0
Nếu ∆’ > 0 thì y’ có hai nghiệm phân biệt x1, x2. Khi đó để y’ ≥ 0, ∀ x < 0 thì ta phải có 0 ≤ x1 < x2. Điều này sẽ không thể xảy ra vì S = x1 + x2 = -2 < 0
Vậy m ≤ -3.
Cách 3:
Phương án B: Với m = -3 ta có y = x3 + 3x2 + 3x + 1 = (x + 1)3. Khi đó y’ = 3(x + 1)3 ≥ 0 ∀ x
Suy ra hàm số đồng biến trên khoảng chừng (-∞;0). Vậy B là đáp án đúng.
Ví dụ 4: Tìm tất cả những giá trị thực của tham số m để hàm số y = x3 – 3mx2 – 9m2x nghịch biến trên khoảng chừng (0;1).A.
B.
C. m < -1
D. hoặc m ≤ -1
Lời giải
Chọn D
Tập xác định D = ℝ
y’ = 3x2 – 6mx -9m2
y’ = 0 ⇔ 3x2 – 6mx -9m2 = 0 ⇔ x2 – 2mx -3m2 = 0
Nếu –m = 3m ⇔ m = 0 thì y’ ≥ 0, ∀ x ∊ ℝ nên hàm số không còn tầm khoảng chừng nghịch biến.
Nếu –m < 3m ⇔ m > 0 thì hàm số nghịch biến trên khoảng chừng (-m; 3m).
Do đó hàm số nghịch biến trên khoảng chừng (0;1)
Kết phù phù hợp với điều kiện ta được
Nếu –m > 3m ⇔ m < 0 thì hàm số nghịch biến trên khoảng chừng (3m; -m)
Do đó hàm số nghịch biến trên khoảng chừng (0;1)
Kết phù phù hợp với điều kiện ta được m ≤ -1
Vậy hàm số nghịch biến trên khoảng chừng (0;1) khi m ≤ -1 hoặc
Dạng 2. Biện luận đơn điệu của hàm phân thức
Phương pháp giải được phân thành 2 loại như sau:
Loại 1. Tìm điều kiện của tham số để hàmTính
– Hàm số đồng biến trên từng khoảng chừng xác định của nó ⇔ y’ > 0 ⇔ ad –cb > 0
– Hàm số nghịch biến trên từng khoảng chừng xác định của nó ⇔ y’ < 0 ⇔ ad –cb < 0
Loại 2. Tìm điều kiện để hàmTính
Hàm số đồng biến trên khoảng chừng (m;n):
Hàm số nghịch biến trên khoảng chừng (m;n):
A. 4
B. Vô số
C. 3
D. 5
Lời giải
Chọn D
D = ℝ m;
Hàm số nghịch biến trên các khoảng xác định khi y’ < 0, ∀ x ∊ D ⇔ mét vuông – 4m < 0 ⇔ 0 < m < 4
Mà m ∊ ℤ nên có 3 giá trị thỏa mãn.
Ví dụ 2. Có bao nhiêu giá trị nguyên của tham số m để hàm sốA. Vô số
B. 4
C. 5
D. 3
Lời giải
Chọn B
Tập xác định D = ℝ 5m
Hàm số nghịch biến trên (10; +∞) khi và chỉ khi
Mà m ∊ ℤ nên m ∊ -2; -1; 0; 1.
Ví dụ 3. Cho hàm sốA. Vô số
B. 3
C. 5
D. 4
Lời giải
Chọn B
hàm số đồng biến trên khoảng chừng xác định khi -1 < m < 3 nên có 3 giá trị của m nguyên
Dạng 3: Tìm m để hàm số khác đơn điệu trên khoảng chừng
Hàm số khác ở đây ám chỉ nhiều chủng loại hàm đa thức bậc cao. Phương pháp chung là đặt ẩn hoặc biến hóa để về những dạng hàm số cơ bản hoặc tính f’ và giải như thông thường.
Ví dụ 1. Có bao nhiêu giá trị nguyên âm của tham số m để hàm sốA. 0
B. 4
C. 5
D. 3
Lời giải
Chọn B
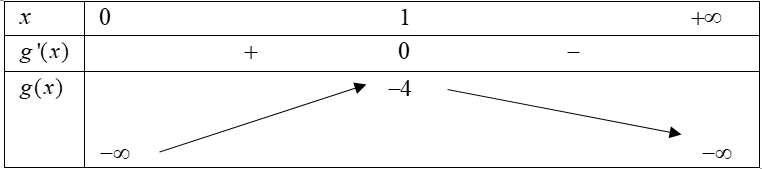
Hàm số đồng biến trên (0; +∞) khi và chỉ khi
Xét hàm số
Bảng biến thiên:
Dựa vào BBT ta có m ≥ -4, suy ra những giá trị nguyên âm của tham số m là -4; -3; -2; -1.
Ví dụ 2. Gọi S là tập hợp tất cả những giá trị của tham số m để hàm sốA.
B. -2
C.
D.
Lời giải
Ta có f’(x) = m2x4 – mx2 + 20x – (mét vuông – m – 20)
= mét vuông(x4 – 1) – m(x2 – 1) + 20(x + 1)
= mét vuông(x – 1)(x + 1)(x2 + 1) – m(x – 1)(x + 1) + 20(x + 1)
= (x + 1)[mét vuông(x – 1)(x2 + 1) – m(x – 1) + 20]
Ta có f’(x) = 0 có một nghiệm đơn là x = -1, do đó nếu (*) không sở hữu và nhận x = -1 là nghiệm thì f’(x) đổi dấu qua x = -1. Do đó để f(x) đồng biến trên ℝ thì f’(x) ≥ 0, ∀ x ∊ ℝ hay (*) nhận x = -1 làm nghiệm (bậc lẻ).
Suy ra: mét vuông (-1 – 1)(1 + 1) – m(-1 – 1) + 20 = 0 ⇔ -4m2 + 2m + 20 = 0
Tổng những giá trị của m là ½
Ví dụ 3. Tập hợp những giá trị thực của tham số m để hàm sốA. [0; 1)
B. (-∞; 0]
C. [0; +∞) 1
D. (-∞; 0)
Lời giải
Chọn B
Tập xác định: D = ℝ 2
Hàm số đã cho đồng biến trên mỗi khoảng chừng xác định của nó khi và chỉ khi:
y’ ≥ 0, ∀ x ∊ D
⇔ m ≤ (x – 2)2, ∀ x ∊ D
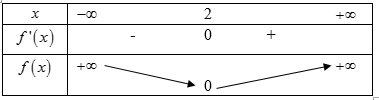
Xét hàm số f(x) = (x – 2)2 ta có:
f’(x) = 2x – 4 ⇒ f’(x) = 0 ⇔ x = 2
Bảng biến thiên:
Vậy, để hàm số đã cho đồng biến trên mỗi khoảng chừng xác định của nó thì m ≤ 0 .
Ví dụ 4. Tìm tất cả những giá trị thực của tham số để hàm sốA.
B.
C. m ≤ 3
D. m < 3
Lời giải
Chọn A
Điều kiện: cos x ≠ m.
Ta có:
Vì x ∊ ⇒ sin x > 0, (cos x – m)2 > 0, ∀ x ∊
; cos x ≠ m.
Để hàm số nghịch biến trên khoảng chừng ⇔ y’ < 0 ∀ x ∊
Chú ý : Tập giá trị của hàm số y = cos x, ∀ x ∊ là (-1; 0)
A. 14
B. 13
C. 12
D. 15
Lời giải
Đặt vì x ∊ (-8; 5)
và
đồng biến trên (-8; 5)
Hàm số trở thành tập xác định D = ℝ m
Để hàm số đồng biến trên khoảng chừng
⇒ m ∊ -9; -8; -7; -6; -5; -4; -1; 0; 4; 5; 6; 7; 8; 9 có 14 giá trị
Dạng 4: Tìm m để hàm số đồng biến nghịch biến trên R
Xét hàm số y = ax3 + bx2 + cx + d ⇒ y’ = 3ax2 + 2bx +c
TH1: a = 0 (nếu có tham số)
TH2: a ≠ 0
Hàm số đồng biến trên ℝ ⇔
Hàm số nghịch biến trên ℝ ⇔
A. (-2; -1)
B. [-2; -1]
C. (-∞; -2) ∪ (-1; +∞)
D. (-∞; -2] ∪ [-1; +∞)
Hướng dẫn giải
Ta có: y’ = -x2 + 2mx + 3m – 2
Hàm số nghịch biến trên ℝ
⇔ mét vuông – 3m + 2 ≤ 0 ⇔ m ∊ [-2; -1]
Đáp án B
Ví dụ 2: Cho hàm số y = ⅓ (m – 1)x3 – (m – 1)x2 – x + 1. Tìm m để hàm số nghịch biến trên ℝ.A. -3 ≤ m ≤ 1
B. 0 ≤ m ≤ 1
C. (0; 1]
D. [0; 1)
Hướng dẫn giải
Ta có: y’ = (m – 1)x2 – 2(m – 1)x – 1
TH1: m – 1 = 0 ⇒ m = 1 ⇒ y’ = -1 < 0. Hàm số nghịch biến trên ℝ.
TH2: m ≠ 1. Hàm số nghịch biến trên ℝ khi:
⇔ m ∊ [0; 1)
Đáp án D
Ví dụ 3: Tìm m để hàm số y = x3 + 2(m + 1) x2 – 3mx + 5m – 2 đồng biến trên ℝ.A.
B.
C.
D.
Hướng dẫn giải
y’ = 3x2 + 4(m + 1) x – 3m
Để hàm số đồng biến trên ℝ thì:
Đáp án A
Dạng 5: Tìm m để hàm số cho bởi đồ thị hàm F(x) đơn điệu
Định nghĩa 1Giả sử K là một khoảng chừng, một đoạn hoặc một nửa khoảng chừng và y = f(x) là một hàm số xác định trên K. Ta nói:
– Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu ∀ x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).
– Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K nếu ∀ x₁, x₂ ∊ K, x1 < x₂ ⇒ f(x₁) > f(x₂)
– Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.
Nhận xét 1Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên D thì hàm số f(x) + g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này hoàn toàn có thể không đúng đối với hiệu f(x) – g(x).
Nhận xét 2Nếu hàm số f(x) và g(x) là những hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số f(x) ∙ g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này hoàn toàn có thể không đúng khi những hàm số f(x), g(x) không là những hàm số dương trên D.
Nhận xét 3Cho hàm số u = u(x), xác định với x ∊ (a;b) và u(x) ∊ (c;d). Hàm số f [u(x)] cũng xác định với x ∊ (a;b). Ta có nhận xét sau:
- Giả sử hàm số u = u(x) đồng biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] đồng biến với x ∊ (a;b) ⇔ f(u) đồng biến với u ∊ (c;d)Giả sử hàm số u = u(x) nghịch biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] nghịch biến với x ∊ (a;b) ⇔ f(u) nghịch biến với u ∊ (c;d)
Giả sử hàm số f có đạo hàm trên khoảng chừng K. Khi đó:
a) Nếu hàm số đồng biến trên khoảng chừng K thì f’(x) ≥ 0, ∀ x ∊ K
b) Nếu hàm số nghịch biến trên khoảng chừng K thì f’(x) ≤ 0, ∀ x ∊ K
Định lý 2Giả sử hàm số f có đạo hàm trên khoảng chừng K. Khi đó:
a) Nếu f’(x) > 0, ∀ x ∊ K thì hàm số f đồng biến trên K.
b) Nếu f’(x) < 0, ∀ x ∊ K thì hàm số f nghịch biến trên K.
c) Nếu f’(x) = 0, ∀ x ∊ K thì hàm số f không đổi trên K.
Chú ýChú ý: Khoảng K trong định lí trên ta hoàn toàn có thể thay thế bởi đoạn hoặc một nửa khoảng chừng. Khi đó phải có thêm giả thuyết “Hàm số liên tục trên đoạn hoặc nửa khoảng chừng đó”. Chẳng hạn:
Nếu hàm số f liên tục trên đoạn [a;b] và f’(x) > 0, ∀ x ∊ K thì hàm số f đồng biến trên đoạn [a;b]
Định lý 3Giả sử hàm số f có đạo hàm trên khoảng chừng K. Khi đó:
a) Nếu f’(x) ≥ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
b) Nếu f’(x) ≤ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f nghịch biến trên K.
Quy tắc xét tính đơn điệu của hàm sốGiả sử hàm số f có đạo hàm trên K
– Nếu f’(x) ≥ 0 với mọi x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm x ∊ K thì hàm số f đồng biến trên K.
– Nếu f’(x) ≤ 0 với mọi x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm x ∊ K thì hàm số f nghịch biến trên K.
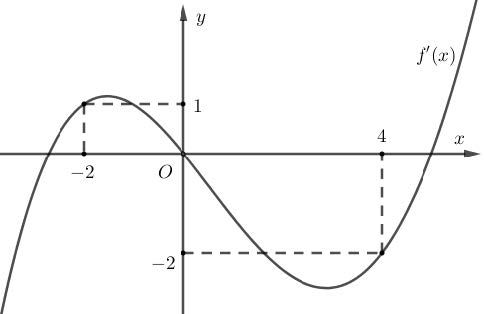
Ví dụ 1. Cho hàm số f(x). Hàm số y = f’(x) có đồ thị như hình sau.Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = 4f(x – m) + x2 – 2mx + 2022 đồng biến trên khoảng chừng (1; 2).
A. 2
B. 3
C. 0
D. 1
Ý tưởng: Phát triển thành bài toán chứa tham số.
Lời giải
Chọn A
Ta có g’(x) = 4f’(x – m) + 2x – 2m
g’(x) ≥ 0 ⇔
Đặt t = x – m thì (*) ⇔
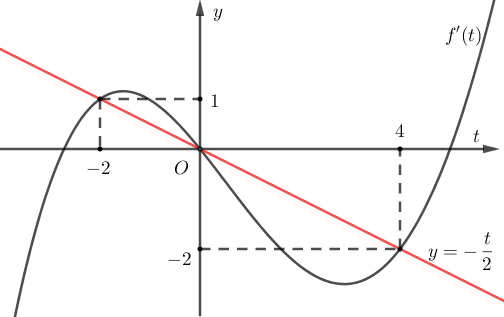
Vẽ đường thẳng trên cùng hệ trục Oxy với đồ thị y = f’(x) như hình vẽ sau:
Từ đồ thị ta có
Hàm số g(x) đồng biến trên khoảng chừng (1; 2) ⇔ g’(x) ≥ 0 ∀ x ∊ (1; 2)
Vì m nguyên dương nên m ∊ 2; 3
Vậy có hai giá trị nguyên dương của m để hàm số g(x) đồng biến trên khoảng chừng (1; 2).
Dạng 6: Tìm m để hàm giá trị tuyệt đối đơn điệu trên khoảng chừng cho trước
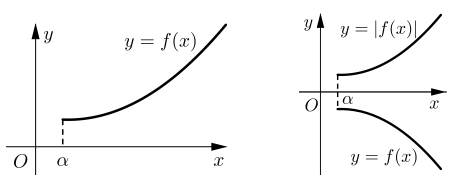
Hàm số y = |f(x)| đồng biến trên [α;+∞) khi và chỉ khi:
Hàm số y = |f(x)| đồng biến trên (α; β) khi và chỉ khi:
Các dạng đồng biến y = |f(x)| trên [α;+∞), (α; β) ta thực hiện tương tự.
Hàm số hỏi nghịch biến làm ngược lại.
Loại 1: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số dạng đa thức đồng biến, nghịch biến trên tập D cho trước.
Ví dụ 1. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = |x5 – 5x2 + 5(m – 1)x – 8| nghịch biến trên khoảng chừng (-∞;1)?A. 2
B. 0
C. 4
D. 1
Lời giải:
Chọn D
Xét hàm số
f(x) = x5 – 5x2 + 5(m – 1)x – 8
TH1: f(x) = 0 có nghiệm x0 ∊ (-∞;1) thì hàm số y = |f(x)| không thể nghịch biến trên khoảng chừng (-∞;1).
TH2: f(x) = 0 không còn nghiệm x0 ∊ (-∞;1)
Ta có: f’(x) = 5x4 – 10x + 5(m – 1)
Khi đó y = |x5 – 5x2 + 5(m – 1)x – 8| = |f(x)| =
Nên
Hàm số nghịch biến trên (-∞;1) khi và chỉ khi y’ ≤ 0 với ∀ x ∊ (-∞;1)
Mà m ∊ ℤ nên m = 3
Ví dụ 2. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |2x3 – mx + 1| đồng biến trên khoảng chừng (1; +∞)?A. 2
B. 6
C. 3
D. 4
Lời giải:
Chọn C
Xét hàm số
f(x) = 2x3 – mx + 1
TH1: f(x) = 0 có nghiệm x0 ∊ (1;+∞) thì hàm số y = |f(x)| không thể nghịch biến trên khoảng chừng (1;+∞).
TH2: f(x) = 0 không còn nghiệm x0 ∊ (1;+∞)
Ta có: f’(x) = 6x2 – m
Khi đó y = |2x3 – mx + 1| = |f(x)| =
Nên
Hàm số nghịch biến trên khoảng chừng (1;+∞) khi và chỉ khi y’ ≥ 0 với ∀ x ∊ (1;+∞)
⇒ m ∊ 1; 2; 3
Ví dụ 3. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số y = |3x4 – 4x3 – 12x2 + m| nghịch biến trên khoảng chừng (-∞; -1)?A. 6
B. 4
C. 3
D. 5
Lời giải
Chọn D
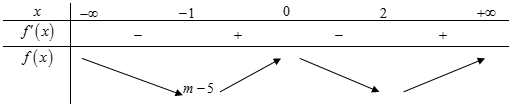
Xét hàm số f(x) = 3x4 – 4x3 – 12x2 + m ⇒ f’(x) = 12x3 – 12x2 – 24x = 12x (x2 – x – 2)
⇒ f’(x) = 0
BBT:
Nhận thấy: Hàm số y = |f(x)| nghịch biến trên khoảng chừng (-∞; -1) ⇔ m – 5 > 0 ⇔ m ≥ 5.
Lại do ⇒ m ∊ 5; 6; 7; 8; 9
Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Loại 2: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số dạng phân thức hữu tỉ đồng biến, nghịch biến trên tập D cho trước.
Ví dụ 1. Tính tổng S tất cả những giá trị nguyên của tham số m trong đoạn [-10; 10] để hàm sốA. S = 55
B. S = 54
C. S = 3
D. S = 5
Lời giải
Chọn B.
Xét hàm số với x ≠ -m – 2, có
Hàm số đồng biến (1; +∞) khi xảy ra một trong hai trường hợp sau:
TH1:
TH2:
Vậy m ∊ (1; +∞), lại do suy ra m ∊ 2; 3; 4; 5; 6; 7; 8; 9; 10
Vậy S = 54
Ví dụ 2. Tìm m để hàm sốA.
B.
C.
D.
Lời giải
Chọn B
Đặt . ĐK: x ≠ -m
Khi đó
Để hàm số đồng biến trên (1;+∞) ⇔
hoặc
Ta có
Vậy ⅓ < m ≤ 1
Ví dụ 3. Có bao nhiêu số nguyên của tham số m để hàm sốA. 4
B. 5
C. Vô số
D. 6
Lời giải
Chọn A
Tập xác định: D = ℝ 1
Xét hàm số
Có
Khi đó
Hàm số đồng biến trên [3; +∞) ⇔ y’ ≥ 0, ∀ x ∊ [3; +∞)
Vì m ∊ ℤ ⇒ m ∊ -2; -1; 0; 1
Vậy có 4 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Loại 3: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số chứa căn đồng biến, nghịch biến trên tập D cho trước.
Ví dụ 1. Cho hàm sốA. 4
B. 2
C. 3
D. 5
Lời giải
Chọn A
Đặt
Ta có
Do hàm số liên tục tại x = 0; x = 1 nên để hàm số nghịch biến trên (0;1) ta xét 2 trường hợp sau:
Trường hợp 1:
Trường hợp 2:
(vô nghiệm)
Do m nguyên nên m nhận những giá trị sau -3; -2; -1; 0
Ví dụ 2. Có bao nhiêu giá trị nguyên của tham số m ∊ (-5; 5) để hàm sốA. 2
B. 3
C. 5
D. 9
Lời giải
Chọn B
Xét hàm số
Ta có
Cho f’(x) = 0
Ta thấy f’(x) < 0, ∀ x ∊ (2; 3) nên hàm số f(x) nghịch biến trên (2; 3)
Để nghịch biến trên (2; 3) thì
f(3) ≥ 0
Do m ∊ (-5; 5) nên m = -2; -3; -4
Ví dụ 3. Có bao nhiêu giá trị nguyên của tham số m ∊ [0; 10] để hàm sốA. 11
B. 10
C. 12
D. 9
Lời giải
Chọn A
Tập xác định D = ℝ
Xét hàm số
Hàm số đồng biến trên khoảng chừng (1;+∞)
TH1:
f’(x) ≥ 0, ∀ x ∊ (1;+∞)
Đặt t = x – 1, t > 0
Xét
Bảng biến thiên:
Từ BBT ta có
TH2:
f’(x) ≤ 0, ∀ x ∊ (1;+∞)
Đặt t = x – 1, t > 0
Mà nên với mỗi giá trị của m luôn có mức giá trị của t dương đủ nhỏ để VT của (*) to hơn 0.
Suy ra không còn mức giá trị nào của m để TH2 thỏa mãn.
Vậy có 11 giá trị nguyên của m thỏa mãn là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
Loại 4: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số lượng giác đồng biến, nghịch biến trên tập D cho trước.
Ví dụ 1. Có bao nhiêu giá trị m nguyên để hàm số y = |f(x)| = |x3 – 3x2 +3(mét vuông + 5) x + (12 – 3m2) cosx| đồng biến trên (0; π)A. 3
B. 5
C. 4
D. Vô số
Lời giải
Chọn B
Đặt h(x) = x3 – 3x2 + 3(mét vuông + 5) x + (12 – 3m2) cosx.
Ta có h’(x) = 3x2 – 6x + 3(mét vuông + 5) – (12 – 3m2) sinx.
⇔ h’(x) = 3(x – 1)2 + 12(1 – sinx) + 3m2(1 + sinx) ≥ 0, ∀ x ∊ (0; π)
Vậy hàm số h(x) luôn đồng biến trên (0; π).
Để y = f(x) đồng biến trên (0; π). Thì h(0) ≥ 0 ⇔ (12 – 3m2) ≥ 0 ⇔ m ∊ [-2; 2]
Kết luận: có 5 giá trị m nguyên thỏa mãn.
Ví dụ 2. Các giá trị của tham số m để hàm số y = |sinx – cosx + m| đồng biến trên khoảng chừngA.
B.
C. m > 1
D. m ≥ 1
Lời giải
Chọn B
Xét hàm số f(x) = sinx – cosx + m =
Khi đó y = |sinx – cosx + m| = |f(x)| = . Nên
Hàm số y = |sinx – cosx + m| đồng biến trên khoảng chừng ⇔ y’ ≥ 0, ∀ x ∊
Với
Nên (1) ⇔ f(x) > 0, ∀ x ∊
A. 1
B. 2
C. 3
D. 0
Lời giải
Chọn A
Trên khoảng chừng , hàm số y = sinx đồng biến
Đặt t = sin x, x ∊ ⇒ t ∊ (0;1)
Khi đó hàm số y = |sin3x – m.sinx + 1| đồng biến trên khoảng chừng khi và chỉ khi
y = g(t) = |t3 – mt + 1| đồng biến trên (0;1)
Xét hàm số y = f(t) = t3 – mt + 1 trên khoảng chừng (0;1) có f’(t) = 3t2 – m.
+) Khi m = 0
f’(t) = 3t2 > 0, ∀ t ⇒ y = f(t) = t3 + 1 đồng biến trên (0;1) và đồng thời y = f(t) = t3 + 1 cắt trục hoành tại điểm duy nhất t = -1
⇒ y = g(t) = |t3 – mt + 1| đồng biến trên (0;1) ⇒ m = 0 thỏa mãn
+) Khi m > 0
f’(t) = 0 có 2 nghiệm phân biệt
Hàm số y = f(t) = t3 – mt + 1 đồng biến trên những khoảng chừng và
TH1: ⇔ 0 < m < 3
Hàm số y = f(t) = t3 – mt + 1 nghịch biến trên khoảng chừng và đồng biến trên khoảng chừng
⇒ Không có mức giá trị của m để y = g(t) = |t3 – mt + 1| đồng biến trên (0;1)
TH2: ⇔ m ≥ 3
Để y = g(t) = |t3 – mt + 1| đồng biến trên (0;1) thì t3 – mt + 1 ≤ 0, ∀ x ∊ (0;1)
⇔ mt ≤ t3 + 1, ∀ x ∊ (0;1)
⇒ Không có mức giá trị của m thỏa mãn
Vậy chỉ có mức giá trị m = 0 thỏa mãn
Ví dụ 4. Có bao nhiêu giá trị nguyên của m thuộc [-5;5] để hàm số y = |cos3x – 3m2cosx| nghịch biến trênA. 1
B. 11
C. 5
D. 6
Lời giải
Chọn B
Đặt t = cos x, vì x ∊ ⇒ t ∊ (0;1)
Vì t =cos x là hàm số nghịch biến trên nên yêu cầu bài toán trở thành tìm m nguyên thuộc [-5;5] để hàm số y = |t3 – 3m2t| đồng biến trên (0;1).
Xét f(t) = t3 – 3m2t, t ∊ (0;1) ⇒ f’(t) = 3t2 – 3m2
TH1: Nếu m = 0 ⇒ f’(t) > 0, ∀ t ∊ (0;1) ⇒ f(t) luôn đồng biến trên (0;1)
Mà f (0) = 0 ⇒ y = |f(t)| luôn đồng biến trên (0; +∞)
⇒ y = |f(t)| luôn đồng biến trên (0;1)
Do đó m = 0 thỏa mãn bài toán (1)
TH2: m ≠ 0 ⇒ f’(t) = 0
*) Với m > 0 , ta có BBT sau:
Từ BBT suy ra hàm số y = |f(t)| luôn đồng biến trên (0; m)
YCBT tương đương (0;1) ⊂ (0; m) ⇔ m ≥ 1 (2)
*) Với m < 0 , ta có BBT sau:
Từ BBT suy ra hàm số y = |f(t)| luôn đồng biến trên (0; -m)
YCBT tương đương (0;1) ⊂ (0; -m) ⇔ m ≤ -1 (3)
Từ (1), (2) và (3) vậy có 11 giá trị nguyên của m thỏa mãn bài toán.
Loại 5: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số mũ đồng biến, nghịch biến trên tập D cho trước.
Ví dụ 1. Có bao nhiêu giá trị nguyên dương của m để y = |9x + 3x – m + 1| đồng biến trên đoạn [0;1]A. 1
B. 4
C. 3
D. 6
Lời giải
Chọn C
Đặt 3x = t ⇒ t ∊ [1;3] vì t ∊ [0;1]
⇒ t = |t2 + t – m + 1| =
Để hàm số đồng biến trên đoạn t ∊ [1;3] thì
Với mọi giá trị của t ∊ [1;3] thì 2t + 1 > 0 nên
Để y’ ≥ 0, ∀ t ∊ [1;3] thì t2 + t – m + 1 ≥ 0, ∀ t ∊ [1;3]
⇒ m – 1 ≤ t2 + t = g(t) , ∀ t ∊ [1;3]
Vậy có 3 giá trị nguyên 1; 2; 3 thỏa mãn yêu cầu bài toán.
Ví dụ 2. Có bao nhiêu giá trị m nguyên dương và nhỏ hơn 2022 để hàm số y = |4x + m.2x+1 + m + 2| đồng biến trên khoảng chừng (0;1)?A. 2022
B. 2022
C. 2
D. 3
Lời giải
Chọn A
Xét hàm số f(x) = 4x + m.2x+1 + m + 2 (1) trên khoảng chừng (0;1)
Đặt t = 2x ⇒ t ∊ (1;2)
Hàm số (1) trở thành h(t) = t2 – 2mt + m + 2 trên khoảng chừng (1;2).
Suy ra h’(t) = 2t – 2m
Ta có y = |f(x)| đồng biến trên khoảng chừng (0;1)
Vì hàm số t = 2x đồng biến trên khoảng chừng (0;1)
Do đó,
Vậy có 2022 số nguyên dương nhỏ hơn 2022 thỏa ycbt.
Ví dụ 3. Cho hàm sốA. 234
B. Vô số
C. 40
D. Không tồn tại m
Lời giải
Chọn C
Đặt
Ta có ⇒ t ∊ (e2; e3), đồng thời x và t sẽ ngược chiều biến thiên.
Khi đó hàm số trở thành y = |t2 + 3t – 2m + 5| = (2)
Ta có:
Hàm số (1) nghịch biến trên khoảng chừng (2;3) ⇔ hàm số (2) đồng biến trên khoảng chừng (e2; e3)
∀ x ∊ (e2; e3)
⇔ t2 + 3t – 2m + 5 > 0 ∀ x ∊ (e2; e3)
∀ x ∊ (e2; e3)
Có ∀ x ∊ (e2; e3)
Với điều kiện m là số nguyên dương ta tìm được 40 giá trị của m.
Ví dụ 4. Có bao nhiêu giá trị nguyên dương m ∊ (-2022; 2022), để hàm số y = |e-x2 + ex2 – m| nghịch biến trên (1;e)?A. 401
B. 0
C. 2022
D. 2022
Lời giải
Chọn A
Đặt f(x) = e-x2 + ex2 – m ⇒ f’(x) = -2xe-x2 + 2ex2
Ta có y = |f (x)| =
Yêu cầu bài toán ⇔ y’ ≤ 0, ∀ x ∊ (1;e) (*)
Vì x ∊ (1;e) nên -2xe-x2 + 2ex2 = , ∀ x ∊ (1;e)
Khi đó, (*) ⇔ f(x) ≤ 0, ∀ x ∊ (1;e)
⇔ e-x2 + ex2 – m ≤ 0, ∀ x ∊ (1;e)
⇔ e-x2 + ex2 ≤ m, ∀ x ∊ (1;e)
Ta có mức giá trị lớn số 1 của hàm số y = e-x2 + ex2 ∀ x ∊ (1;e) là e-x2 + ex2
Nên m ≥ e-x2 + ex2 ≈ 1618,18
Vậy có 401 giá trị nguyên dương m thỏa mãn.
Loại 6: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số logarit đồng biến, nghịch biến trên tập D cho trước.
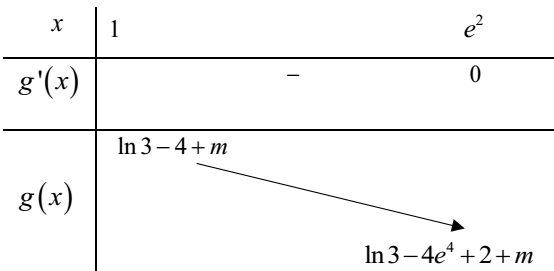
Ví dụ 1. Có bao nhiêu giá trị nguyên thuộc khoảng chừng (-100; 100) của tham số m để hàm số y = |ln3x – 4x2 + m| đồng biến trên đoạn [1;e2]?A. 101
B. 102
C. 103
D. 100
Lời giải
Chọn B
y = |ln3x – 4x2 + m|. Điều kiện x > 0
Xét hàm số g(x) = ln3x – 4x2 + m trên [1;e2]
⇒ g(x) nghịch biến trên [1;e2]
⇒ Hàm số y = |g(x)| = |ln3x – 4x2 + m| đồng biến trên đoạn [1;e2]
⇔ ln3 – 4 + m ≤ 0 ⇔ m ≤ 4 – ln3
Mà m nguyên thuộc khoảng chừng (-100; 100) nên m ∊ -99; -98;…; -1; 0; 1; 2
Vậy có 102 giá trị m nguyên thỏa mãn yêu cầu bài toán.
Ví dụ 2. Có bao nhiêu số nguyên m < 2022 để hàm số y = |ln(mx) – x + 2| nghịch biến trên (1;4)?A. 2022
B. 2022
C. 1
D. Vô số.
Lời giải
Chọn A
Xét f(x) = ln(mx) – x + 2.
Dễ thấy ∀ x ∊ (1;4): mx > 0 ⇔ m > 0
Khi đó
Do đó f(x) luôn nghịch biến trên (1;4)
Yêu cầu bài tóan tương đương với f(4) ≥ 0 ⇔ ln(4m) – 2 ≥ 0
Vậy m ∊ [2; 2019] có 2022 số nguyên thỏa mãn.
Ví dụ 3. Có bao nhiêu số nguyên m thuộc (-2022; 2022) để hàm số y = |ln(x2 + 2x – m) – 2mx2 – 1| luôn đồng biến trên (0;10)?A. 4038
B. 2022
C. 2022
D. 2022
Lời giải
Chọn C
Ta xét hàm số f(x) = ln(x2 + 2x – m) – 2mx2 – 1 trên (0;10)
Điều kiện hàm số nghĩa là x2 + 2x – m > 0, ∀ x ∊ (0;10)
⇔ x2 + 2x > m, ∀ x ∊ (0;10) (1)
Ta lại sở hữu x2 + 2x = x.(x + 2) > 0 với ∀ x ∊ (0;10) nên điều kiện (1) cho ta m ≤ 0 (2)
Đạo hàm do m ≤ 0 và x ∊ (0;10) nên
Suy ra f’(x) > 0 hàm số đồng biến trên (0;10).
Từ đó để hàm số y = |ln(x2 + 2x – m) – 2mx2 – 1| = |f(x)| đồng biến trên (0;10) điều kiện đủ là f(x) ≥ 0 với ∀ x ∊ (0;10) (3)
+) TH1: Xét m = 0
Khi đó f(x) = ln(x2 + 2x) – 1 có không thỏa mãn (3)
+) TH2: Xét m < 0
Do hàm số f(x) đồng biến nên ta chỉ việc f(0) ≥ 0 ⇔ ln(-m) – 1 ≥ 0 ⇔ -m ≥ e ⇔ m ≤ -e
Từ đó ta được:
⇔ m ∊ -2022; -2022; -2022;…; -3 có 2022 giá trị m thỏa mãn bài toán.
Ví dụ 4. Có bao nhiêu số nguyên của tham số m trong đoạn [-3;3] để hàm số y = |ln(x3 + mx + 2)| đồng biến trên nửa khoảng chừng [1;3)?A. 7
B. 4
C. 6
D. 5
Lời giải
Chọn C
Điều kiện xác định: x3 + mx + 2 > 0
Xét hàm số f(x) = ln(x3 + mx + 2)
Ta có:
Hàm số đồng biến trên nửa khoảng chừng [1;3)
Trường hợp 1:
Trường hợp 2:
Từ hai trường hợp trên suy ra m ≥ -2
Mà m ∊ [-3;3] ⇒ m ∊ -2; -1; 0; 1; 2; 3
Vậy có 6 số nguyên m thỏa mãn YCBT.
Tài liệu tìm m để hàm số đồng biến, nghịch biến trên khoảng chừng
tin tức tài liệuTác giảThầy Nguyễn Bảo VươngSố trang59Lời giải chi tiếtCóMục lục tài liệu:
- Dạng 1. Tìm khoảng chừng đơn điệu của hàm số thông qua bảng biến thiên, đồ thịDạng 2. Tìm khoảng chừng đơn điệu của hàm số cho trướcDạng 3. Tìm m để hàm số đơn điệu trên những khoảng chừng xác định của nóDạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng chừng cho trướcDạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng chừng cho trướcDạng 6. Tìm m để hàm số khác đơn điệu trên khoảng chừng cho trướcDạng 7. Tìm khoảng chừng đơn điệu của hàm số f(u) lúc biết đồ thị hàm số f’(x)Dạng 8. Tìm khoảng chừng đơn điệu của hàm số f(u)+g(x) lúc biết đồ thị, bảng biến thiên của hàm số f’(x)
Thầy Dũng dạy toán học từ năm 2010 sau khi nhận bằng sư phạm môn toán tại trường Đại Học Sư Phạm Đà Nẵng. Triết lý dạy học của thầy luôn coi trọng chất lượng hơn số lượng bởi ở một góc nhìn nào đó, tất cả chúng ta sử dụng toán học hằng ngày trong môi trường tự nhiên thiên nhiên sống đời thường và nên phải làm rõ về bản chất của nó thay vì học sơ sài. Thầy cảm hứng rất như mong ước khi được làm sửa đổi và biên tập viên cho môn toán tại VerbaLearn, nơi mà những bài dạy của thầy hoàn toàn có thể tiếp cận nhiều học viên hơn.
[embed]https://www.youtube.com/watch?v=RhYbEVK8oNM[/embed]