Mẹo về Một byte hoàn toàn có thể màn biểu diễn tới đã bao nhiêu số nguyên có dấu Mới Nhất
Bùi Thị Thu Hương đang tìm kiếm từ khóa Một byte hoàn toàn có thể màn biểu diễn tới đã bao nhiêu số nguyên có dấu được Update vào lúc : 2022-04-09 14:55:09 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Câu hỏi: Một byte màn biểu diễn của số nguyên có dấu trong phạm vi từ
A. -127 đến 127 B. -127 đến 128 C. -128 đến 128
D. -128 đến 127
Đáp án A.
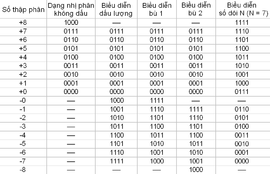
Một byte màn biểu diễn được số nguyên có dấu trong phạm vi từ -127 đến 127. Một byte 8 bit hoàn toàn có thể biểu thị được 256 giá trị rất khác nhau (28 = 256) – đủ để tàng trữ một số trong những nguyên không dấu từ 0 đến 255, hay một số trong những nguyên có dấu từ -127 đến 127.
Trong toán học, những số âm (bất kể thuộc hệ cơ số nào) đều được màn biểu diễn bằng phương pháp thông thường là đặt trước số dương tương ứng một dấu "−" (trừ). Ví dụ: với hệ thập phân, số nguyên âm năm được màn biểu diễn là −5. Tuy nhiên, trong máy tính, khi mọi ký hiệu, số lượng,... đều được màn biểu diễn dưới hệ nhị phân thông qua hai chữ số 0 và 1 thì mọi chuyện lại trở nên phức tạp hơn.
Có nhiều cách thức được sử dụng để màn biểu diễn số âm trong máy tính. Bài này chỉ ra mắt bốn phương pháp đa phần nhất, đó là: phương pháp dấu lượng (sign-and-magnitude), bù 1, bù 2 và số quá N (excess-N).
Các máy tính lúc bấy giờ hầu hết đều sử dụng phương pháp màn biểu diễn số bù 2. Tuy nhiên, trong vài tình huống, những phương pháp khác vẫn hoàn toàn có thể được sử dụng.
Phương pháp dấu lượng dùng bit cực trái làm bit dấu (sign bit) – tức đại diện cho dấu của số – theo quy ước: nếu bit dấu là một trong thì số là số âm (1 tương đương với dấu "-"), ngược lại, nếu nó là 0 thì số là số dương (0 tương đương với dấu "+"). Các bit còn sót lại được dùng để màn biểu diễn độ lớn của số (hay giá trị tuyệt đối – absolute value – của số).
Để màn biểu diễn một số trong những âm về dạng nhị phân có dấu với mẩu K bit là lấy số cần màn biểu diễn thêm vào đó 2K-1 sau đó màn biểu diễn chúng ở hệ nhị phân
Theo phương pháp này, một byte 8 bit sẽ có 7 bit (trừ đi bit dấu) được dùng để màn biểu diễn cho những số có mức giá trị từ 0000000 (010) đến 1111111 (12710). Khi sử dụng bit dấu, ý nghĩa của 7 bit trên sẽ thay đổi, và ta hoàn toàn có thể màn biểu diễn những số từ −12710 đến +12710. Trong phương pháp dấu lượng, số 0 hoàn toàn có thể được màn biểu diễn ở hai dạng, đó là 00000000 (+0) và 10000000 (−0).
Ví dụ: giả sử mẫu 8 bit, khi sử dụng phương pháp dấu lượng, số 510 được màn biểu diễn sang hệ nhị phân là: 0000 0101, còn số −5 là 1000 0101.
So sánh với cách màn biểu diễn số âm mà ta thường sử dụng, ta thấy phương pháp dấu lượng có nhiều điểm tương đồng. Trong hệ thập phân, khi muốn màn biểu diễn số có dấu, ta đặt dấu cần màn biểu diễn ngay trước giá trị tuyệt đối của số. Phương pháp dấu lượng cũng đặt dấu ngay trước giá trị tuyệt đối của số, chỉ có khác ở chỗ thay dấu "+" bằng "0" và "−" bằng "1". Có lẽ vì sự tương đồng này, một vài máy tính thế hệ đầu tiên (như IBM 7090) đã sử dụng phương pháp dấu lượng khi màn biểu diễn số âm.
Phương pháp bù 1 màn biểu diễn số âm theo cách sau:
- Thứ nhất, bit dấu 0 nếu số là số dương, và 1 nếu số là số âm.
Thứ hai, sử dụng toán tử thao tác bit (bitwise) NOT để đảo tất cả những bit của số nhị phân dương (tính bit dấu) để màn biểu diễn số âm tương ứng.
Như vậy, phương pháp bù 1 hoàn toàn in như phương pháp dấu lượng, duy chỉ khác ở cách màn biểu diễn độ lớn của số.
Ví dụ: dạng bù 1 của 00101011 (43) là 11010100(−43) (xem bài chính về bù 1 để biết phương pháp màn biểu diễn số thập phân sang nhị phân bằng phương pháp bù 1).
Giống phương pháp dấu lượng, một byte 8 bit áp dụng phương pháp bù 1 cũng hoàn toàn có thể màn biểu diễn những số từ −12710 đến +12710 (để ý quan tâm: đã mất đi một bit dùng làm bit dấu). Bù 1 cũng luôn có thể có hai dạng màn biểu diễn cho số 0, gồm có: 00000000 (+0) và 11111111 (−0) (mẫu 8 bit).
Khi thực hiện phép cộng giữa hai số màn biểu diễn theo phương pháp bù 1, ta cũng thực hiện theo quy tắc cộng nhị phân thông thường, tuy nhiên, sau khi đã thực hiện xong, nếu còn phát sinh bit nhớ thì phải tiếp tục cộng bit nhớ này vào kết quả vừa thu được. Về vấn đề này, xin xem thêm ở bài chính về bù 1.
Phương pháp màn biểu diễn số bù 1 được sử dụng rộng rãi trong những thế hệ máy tính cũ, điển hình là những dòng máy PDP-1 và UNIVAC 1100/2200.
Trong phương pháp bù 2, những số âm được màn biểu diễn in như phương pháp bù 1, tuy nhiên, phải thêm vào đó 1 vào kết quả (ở hệ nhị phân).
Ví dụ: số −510 được màn biểu diễn sang hệ nhị phân (xét mẫu 8 bit) sử dụng phương pháp bù 1 là 11111010. Để màn biểu diễn theo phương pháp bù 2, ta thêm vào đó 1 vào số nhị phân ở bù 1, tức cộng 1 cho 11111010: 11111010 + 1 = 11111011. Vậy 11111011 là màn biểu diễn bằng bù 2 của −510 trong máy tính.
Phương pháp màn biểu diễn số bù 2 ra đời khi người ta gặp vấn đề với hai phương pháp dấu lượng và bù 1, đó là:
- Có hai cách màn biểu diễn cho số 0.
Bit nhớ phát sinh sau khi đã thực hiện phép tính phải được cộng tiếp vào kết quả.
Với phương pháp bù 2, số 0 chỉ có một cách màn biểu diễn duy nhất là 00000000 (mẫu 8 bit). Việc đổi dấu một số trong những – kể cả từ âm sang dương hay từ dương sang âm – đều được thực hiện theo cùng một cách, đó là: đảo tất cả những bit rồi thêm vào đó một vào kết quả. Việc thực hiện phép cộng với số màn biểu diễn theo phương pháp bù 2 được thực hiện hoàn toàn in như cộng hai số nhị phân thông thường, tuy nhiên, khi phát sinh bit nhớ ở bit dấu, ta hoàn toàn có thể bỏ nó đi. Về vấn đề này, xin xem thêm ở bài chính về bù 2.
Với mẫu 8 bit, phương pháp bù 2 hoàn toàn có thể màn biểu diễn tốt những số nguyên có mức giá trị từ −12810 đến +12710 (so với từ −12710 đến +12710 theo phương pháp dấu lượng và bù 1) do được lợi từ việc tiết kiệm được một cách màn biểu diễn số 0 (không phân biệt giữa −0 và +0).
Phương pháp màn biểu diễn số quá N – còn được gọi là màn biểu diễn số dịch (biased representation) – sử dụng một số trong những nguyên N cho trước làm giá trị dịch ("dịch" hiểu nôm na theo nghĩa "sự dịch chuyển" hay "sự thiên lệch"). Theo phương pháp này, một giá trị thập phân (tức giá trị cần màn biểu diễn) sẽ được màn biểu diễn bằng dạng nhị phân của một số trong những dương nào đó sao cho, giá trị của số dương này to hơn giá trị cần màn biểu diễn N đơn vị.
Ví dụ: giả sử cần màn biểu diễn giá trị 210 theo số quá 5 (mẫu 8 bit):
- Bước 1: ta có:
- Giá trị cần màn biểu diễn: 2.
N = 5.
Vậy 210 sẽ được màn biểu diễn bằng dạng nhị phân của 7: 00000111.
Theo ví dụ trên, ta sẽ có bảng sau:
Số thập phân cần màn biểu diễn Giá trị thập phân của số quá 5 Do đó, số thập phân sẽ được màn biểu diễn thành −5 0 00000000 −4 1 00000001 −3 2 00000010 −2 3 00000011 −1 4 00000100 0 5 00000101 1 6 00000110 2 7 00000111 3 8 00001000 4 9 00001001 5 10 00001010 6 11 00001011 7 12 00001100 8 13 00001101 9 14 00001110 10 15 00001111Ta thấy, 0 được màn biểu diễn bằng nhị phân của 5, và −5 được màn biểu diễn bằng nhị phân của 0. Tổng quát, 0 được màn biểu diễn bằng nhị phân của N, còn −N được màn biểu diễn bằng mẫu có tất cả những bit đều là 0.
Phương pháp này ngày này còn được sử dụng rộng rãi để màn biểu diễn những số chấm động (floating point number), tiêu biểu là chuẩn số chấm động IEEE. Theo chuẩn này, những số chấm động có độ đúng chuẩn đơn (single-precision) 32 bit (như kiểu float của Java) có phần mũ (đó đó là số lượng ký số của phần nằm sau dấu chấm thập phân) được màn biểu diễn bằng số quá 127 với mẫu 8 bit, và những số chấm động có độ đúng chuẩn đôi (double-precision) 64 bit (như kiểu double của Java) có phần mũ màn biểu diễn bằng số quá 1023 với mẫu 11 bit.
- Bù 1
Bù 2
Số quá 3
[embed]https://www.youtube.com/watch?v=Yht0pccYbIk[/embed]