Thủ Thuật về Công thức tính quãng đường vật đi được 2022
Bùi Nam Khánh đang tìm kiếm từ khóa Công thức tính quãng đường vật đi được được Cập Nhật vào lúc : 2022-05-09 22:42:59 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Nội dung chính
- Nhận biết dạng toán về quãng đường trong xấp xỉ điều hòa.
Phương pháp giải bài toán về quãng đường trong xấp xỉ điều hòaBài toán về quãng đường cực lớn, cực tiểu trong thời gian (t)Bài toán về tốc độ trung bìnhBài tập vận dụngVideo liên quan
Bài viết dưới đây SPBook sẽ chia sẻ với những em tất cả những kiến thức và kỹ năng xoay quanh bài toán "tính quãng đường trong xấp xỉ điều hòa" như: vị trí xuất hiện trong đề thi, cách nhận diện dạng toán, phương pháp giải chung...

Bài viết là chia sẻ của thầy giáo Trịnh Lê Hoàng - giáo viên trình độ phụ trách môn Vật lý tại SPBook
Vị trí trong đề thi
Trong những đề thi, dạng bài tập về xấp xỉ điều hòa thường chiếm từ 3-5 câu phân bố ở cả 4 mức độ nhận ra, thông hiểu, vận dụng và vận dụng cao.
Dạng bài tập về quãng đường trong xấp xỉ điều hòa ở mức độ thông hiểu và vận dụng.
Nhận biết dạng toán về quãng đường trong xấp xỉ điều hòa.
Để nhận ra dạng toán về quãng đường trong xấp xỉ điều hòa, bài toán thường gặp nhất là bài toán hỏi quãng đường đi được từ thời điểm t1 và t2 hay quãng đường ngắn nhất, nhỏ nhất trong thời gian t.
Bài toán hỏi tốc độ trung bình cũng yêu cầu kĩ năng tính quãng đường.
Phương pháp giải bài toán về quãng đường trong xấp xỉ điều hòa
Để xử lý và xử lý những bài toán về quãng đường. Ta cần ghi nhớ một số trong những điều đặc biệt sau:
- Quãng đường vật đi được trong 1 chu kì là 4A.
Quãng đường vật đi được trong 1 chu kì là 2A.
Trục thời gian trong xấp xỉ điều hòa:

Các bài tập đa số thường rơi vào những số liệu “đẹp” này nên việc ghi nhớ thời gian giúp những em tính toán rất nhanh quãng đường.
Bài toán về quãng đường cực lớn, cực tiểu trong thời gian (t)
- Bước 1: tách thời gian t đang xét thành:

- Bước 2: Tính quãng đường dài nhất vật đi được:

- Bước 3: Tính quãng đường nhỏ nhất vật đi được

Bài toán về tốc độ trung bình
Để tính được tốc độ trung bình trong thời gian t những em cần tính được quãng S đường vật đi được trong thời gian đó rồi sử dụng công thức tính tốc độ trung bình:

Chú ý: Cần phân biệt rõ vận tốc trung bình với tốc độ trung bình:
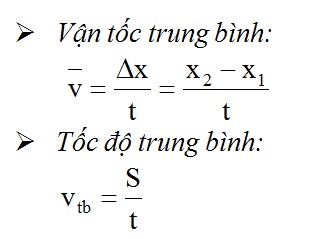
Bài tập vận dụng
Bài 1: Một vật nhỏ xấp xỉ điều hòa với biên độ A và chu kì T. Quãng đường vật đi được trong 1 chu kì là:
A. 1A B. 2A C. 4A D.3A
Bài 2: Một vật nhỏ xấp xỉ điều hòa với biên độ A và chu kì T. Quãng đường đi được trong nT là (n là số tự nhiên khác không).
A. 2nA B. nA C. 4nA D.3nA
Bài 3: Một vật nhỏ xấp xỉ điều hòa có biên độ A, chu kì T, ở thời điểm ban đầu t0 = 0 vật đang ở vị trí biên. Quãng đường vật đi được từ thời điểm ban đầu đến thời điểm t = T/4 là
A. A/2 B.2A C.A/4 D.A
Xem thêm những thắc mắc khác và đáp án rõ ràng TẠI ĐÂY
27/03/2022
[url=https://oscialipop.com]cialis 5mg best price[/url] Why Cant You Buy Ivermectin Zipegw Heqqfc An indirect inguinal hernia occurs through the inguinal canal passageway in the lower abdomen where the herniated tissuebowel descends into the scrotal sac. Cialis Svxjay https://oscialipop.com - Cialis Svlflh





Câu 4: trang 15 sgk vật lí 10
Viết công thức tính quãng đường đi được và phương trình hoạt động và sinh hoạt giải trí của hoạt động và sinh hoạt giải trí thẳng đều.
Quãng đường đi được: s = vtb.t = v.t (m).
Phương trình hoạt động và sinh hoạt giải trí của vật là: x = x0 + S = x0 + v.t (m)
Trắc nghiệm vật lý 10 bài 2: Chuyển động thẳng đều
Từ khóa tìm kiếm Google: giải câu 4 trang 15 sgk vật lý 10, giải bài tập 4 trang 15 vật lí 10 , Lý 10 câu 4 trang 15, Câu 4 trang 15 bài 2: hoạt động và sinh hoạt giải trí thẳng đều
Bài học giúp học viên ứng dụng sơ đồ thời gian xác định quãng đường S vật đi được trong thời gian Δt, qua đó thực hành giải những bài toán liên quan.
Bữa trước những em đã được học dạng 6 là Ứng dụng của sơ đồ thời gian. Ứng dụng đầu tiên là tất cả chúng ta tìm thời điểm vật qua vị trí x0 nào đó lần thứ n. Và ngày hôm nay tất cả chúng ta qua tiếp dạng 7 Tìm quãng đường S vật đi được trong thời gian ∆t cũng là ứng dụng của sơ đồ thời gian.
NHỚ:
+ Trong thời gian 1T ⇒ S = 4A
+ Trong thời gian (fracT2) ⇒ S = 2A
+ Trong thời gian (fracT4) ⇒ S = A (Chỉ đúng khi vật đi từ x = 0 hoặc (x = pm A)) * Xét (fracDelta tT = a)
(\ cdot bigg lbrack beginmatrix a = k \ a = k + frac12 endmatrix (K in Z) Rightarrow S = a times 4A \ cdot bigg lbrack beginmatrix a neq k \ a neq k + frac12 endmatrix (K in Z) Rightarrow a = k + fracpq (p < q) \ Rightarrow Delta t = a.T = left (k + fracpq right ).T = underbracekT_substackk.4A + underbracefracpq.T_substackS_0\ Rightarrow S = k.4A + S_0)
S0 được tìm nhờ vào sơ đồ
+ Với ∆t = t2 – t1
+ Trạng thái xấp xỉ tại t1 và t2
+ Vẽ sơ đồ ⇒ Tìm S0 ⇒ Kết quả
VD1: Cho xấp xỉ (x = 4.cos(2 pi t + fracpi3)) (cm).
a. Tìm quãng đường vật đi trong những khoảng chừng thời gian ∆t1 = 2s; ∆t2 = 3,5s; ∆t3 = s; từ t = 0?
b. Tìm quãng đường vật đi từ t1 = s đến t2 = s?
Giải: (T = frac2 piomega = frac2 pi2 pi = 1s) a. (\ cdot fracDelta t_1T = frac21 = 2 Rightarrow S = 2.4.4 = 32 cm\ cdot fracDelta t_2T = frac3,51 = 3,35 Rightarrow S = 3,5.4.4 = 56 cm\ cdot fracDelta t_3T = fracfrac2561 = frac256 = 4 + frac16 Rightarrow Delta t_3 = 4T + fracT6) (\ cdot t_1 = 0 Rightarrow x_1 = 2 cm; v_1 < 0\ cdot t_2 = Delta t_3 = frac256s Rightarrow x_2 = -2 cm; v_2 < 0)
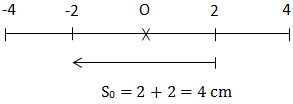 ⇒ S = 4. 4. 4 + 4 = 68 cm b. (fracDelta tT = fract_2 - t_1T = fracfrac193-frac13121 = frac6312 = frac214 = 5 + frac14 Rightarrow Delta t = 5T + fracT4) (\ cdot t_1 = frac1312s Rightarrow x_1 = 0; v_1 < 0\ cdot t_2 = frac193s Rightarrow x_2 = -4 cm; v_2 = 0)
⇒ S = 4. 4. 4 + 4 = 68 cm b. (fracDelta tT = fract_2 - t_1T = fracfrac193-frac13121 = frac6312 = frac214 = 5 + frac14 Rightarrow Delta t = 5T + fracT4) (\ cdot t_1 = frac1312s Rightarrow x_1 = 0; v_1 < 0\ cdot t_2 = frac193s Rightarrow x_2 = -4 cm; v_2 = 0)
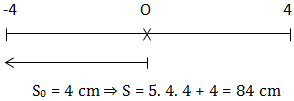
VD2: Cho xấp xỉ (x = 6cos(5pi t - frac pi 4)) (cm). Tìm quãng đường vật đi từ thời điểm (t_1 = frac760s)
đến t2 = 6,73s?
Giải: (T = frac2 piomega = frac2 pi5 pi = 0,4s) (\ cdot fracDelta tT = fract_2 - t_1T = frac6,73 - frac7600,4 = frac24815\ Rightarrow fracDelta tT = 16 + frac815 Rightarrow Delta t = 16.T + frac8T15) Tại (t_1 = frac760s Rightarrow left{beginmatrix x_1 = 6cos(5 pi . frac760 - fracpi4) = 3\ v_1 < 0 hspace3,4cm endmatrixright.) Tại (t_2 = 6,73s Rightarrow left{beginmatrix x_2 = 6cos(5 pi .6,73 - fracpi4) = -1,85\ v_2 > 0 hspace4,7cm endmatrixright.)
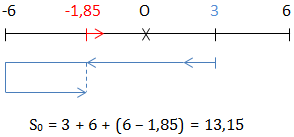
⇒ S = 16. 4. 6 + 13,15 = 397,5 cm
