Thủ Thuật về Có bao nhiêu trường hợp bằng nhau của hai tam giác thường. a. 2 b. 4 c. 3 d. 1 Chi Tiết
Bùi Đình Hùng đang tìm kiếm từ khóa Có bao nhiêu trường hợp bằng nhau của hai tam giác thường. a. 2 b. 4 c. 3 d. 1 được Update vào lúc : 2022-05-27 09:00:10 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.Giới thiệu về cuốn sách này
Nội dung chính- Các trường hợp bằng nhau của tam giác A. 4 Trường hợp bằng nhau của tam giác vuôngB. Bài tập về những trường hợp bằng nhau của tam giácC. Ví dụ minh họa những trường hợp bằng nhau của tam giác vuôngD. Bài tập trường hợp bằng nhau của tam giác vuôngVideo liên quan
Giới thiệu về cuốn sách này
1.687 lượt xem
Các trường hợp bằng nhau của tam giác
GiaiToan.com xin ra mắt đến quý thầy cô và học viên tài liệu Trường hợp bằng nhau của tam giác vuông. Tài liệu gồm có lý thuyết và bài tập được xây dựng dựa theo trọng tâm kiến thức và kỹ năng Toán 7 giúp những em học viên ôn tập những kiến thức và kỹ năng về những trường hợp bằng nhau của tam giác như cạnh - góc - cạnh, cạnh huyền góc nhọn, cạnh huyền cạnh góc vuông, ...để sẵn sàng sẵn sàng cho những bài thi học kì đạt hiệu suất cao nhất. Sau đây mời những bạn học viên cùng tham khảo tải về bản đầy đủ rõ ràng.
A. 4 Trường hợp bằng nhau của tam giác vuông
Trường hợp 1: Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (c – g – c).
Ví dụ:
Xét tam giác vuông ABC và tam giác vuông FHI có:
AB = HF
BC = HI
=> ∆ABC = ∆FHI (c – g – c)
Trường hợp 2: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g – c – g)
Ví dụ:
Xét tam giác vuông ABC và tam giác vuông FHI có:
BC = HI
=> ∆ABC = ∆FHI (g – c - g)
Trường hợp 3: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh huyền – góc nhọn)
Ví dụ:
Xét tam giác vuông ABC và tam giác vuông FHI có:
AC = FI
=> ∆ABC = ∆FHI (cạnh huyền – góc nhọn)
Trường hợp 4: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông kia thì hai tam giác vuông đó bằng nhau (cạnh huyền – cạnh góc vuông)
Ví dụ:
Xét tam giác vuông ABC và tam giác vuông FHI có:
BC = HI
AB = FH
=> ∆ABC = ∆FHI (cạnh huyền – cạnh góc vuông)
B. Bài tập về những trường hợp bằng nhau của tam giác
Bài 1: Cho tam giác ABC vuông tại A, phân giác BE (Điểm E thuộc cạnh AC), đường thẳng qua E vuông góc với BC tại D và cắt tia BA tại F
a. Chứng minh hai tam giác EAB và EDB bằng nhau.
b. So sánh EA và EC va chứng tỏ EC = EF
c. Gọi O là giao điểm của đường thẳng BE và CE. Chứng minh OA = OD
Bài 2: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc BC.
c) Chứng minh AM là phân giác của góc A
Bài 3: Cho hình vẽ, biết
Chứng minh rằng:
a. ∆ABD = ∆ACD
b. ∆DBE = ∆DCH
c. ∆ABH = ∆ACE
Bài 4: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm H sao cho BH = BA.
a) Chứng minh ∆ABD = ∆HBD
b) Chứng minh DH vuông góc với BC
c) Giả sử góc
. Tính số đo góc ADBBài 5: cho tam giác ABC vuông tại B, đường phân giác AD (D thuộc BC). Kẻ BO vuông góc với AD (O thuộc AD), BO cắt AC tại E. Chứng minh:
a. ∆ABO = ∆AEO
b. ∆BAE cân
c. AD là đường trung trực của BE
d. Kẻ BK vuông góc với AC (K ∈ AC). Gọi M là giao điểm của BK và AD. Chứng minh rằng ME// BC
------------------------------------------------------------
Trên đây GiaiToan đã ra mắt đến bạn đọc những kiến thức và kỹ năng quan trọng cần lưu ý về Chuyên đề Tam giác vuông giúp học viên nắm vững kiến thức và kỹ năng, áp dụng vào những bài tập, bài kiểm tra trong học kì sắp tới. Chúc những bạn học tập tốt!
Khách
Hãy nhập thắc mắc của bạn vào đây
Dưới đây là một vài thắc mắc hoàn toàn có thể liên quan tới thắc mắc mà bạn trình lên. Có thể trong đó có câu vấn đáp mà bạn cần!
Chuyên đề Toán học lớp 7
Các trường hợp bằng nhau của tam giác vuông là gì? Dấu hiệu nhận ra những trường hợp bằng nhau của hai tam giác vuông ra làm sao? Là thắc mắc được rất nhiều bạn học viên quan tâm. Chính vì vậy ngày hôm nay Download muốn ra mắt đến quý thầy cô và những bạn toàn bộ kiến thức và kỹ năng về những trường hợp bằng nhau của tam giác vuông.
Tài liệu gồm có khái niệm hai tam giác bằng nhau, những trường hợp bằng nhau của 2 tam giác vuông kèm theo một số trong những ví dụ minh họa và bài tập. Hi vọng thông qua nội dung bài viết này những em học viên củng cố ôn luyện kiến thức và kỹ năng đã học để nhanh gọn giải được những bài tập Hình học 7. Bên cạnh đó những bạn xem thêm một số trong những tài liệu như: tổng hợp kiến thức và kỹ năng môn Toán lớp 7, tính chất trực tâm trong tam giác, Các trường hợp bằng nhau của hai tam giác và rất nhiều tài liệu khác tại phân mục Toán 7.
Hai tam giác bằng nhau là hai tam giác có những cạnh tương ứng bằng nhau, những góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C".
*Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )
*Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )
*Cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)
*Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
C. Ví dụ minh họa những trường hợp bằng nhau của tam giác vuông
Ví dụ 1:
Cho ΔABC cân ở A (∠A < 90o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).
a) Chứng minh rằng AH = HK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A
Trả lời
Vẽ hình minh họa:
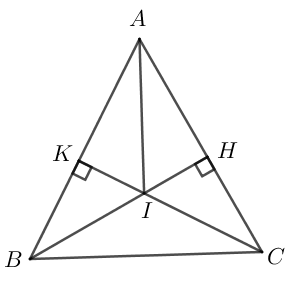
a) ΔABC cân tại A (giả thiết)
Suy ra
AB = AC (tính chất)
(định lí)Xét hai tam giác vuông HAB và KAC, ta có:
AB = AC (chứng tỏ trên)
chung⇒ ΔHAB = ΔKAC (cạnh huyền - góc nhọn)
⇒ AH = AK (cặp cạnh tương ứng)
b) Xét hai tam giác vuông KAI và HAI, ta có:
AH = AK (chứng tỏ trên)
AI cạnh chung
⇒ ΔHAI = ΔKAI (cạnh huyền - cạnh góc vuông)
(cặp góc tương ứng)Hay AI là tia phân giác của
Ví dụ 2: Các tam giác vuông ABC và DEF có góc A = góc D = 90o, AC = DF. Hãy tương hỗ update thêm một điều kiện bằng nhau để ΔABC = ΔDEF.
Trả lời
+ Bổ sung AB =DE thì ΔABC = ΔDEF (cạnh - góc - cạnh)
+ Bổ sung
thì ΔABC = ΔDEF (góc - cạnh - góc)+ Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền - cạnh góc vuông)
Ví dụ 3: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng
a) HB = HC
b) góc BAH = góc CAH
Trả lời
a) Xét hai tam giác vuông ΔABH và ΔACH có:
AB = AC (giả thiết)
AH cạnh chung
⇒ ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)
Suy ra HB = HC (cặp cạnh tương ứng)
b) Ta có ΔABH = ΔACH (chứng tỏ trên)
(cặp góc tương ứng)D. Bài tập trường hợp bằng nhau của tam giác vuông
I. Lý thuyết:
Câu 1: Phát biều những trường hợp bằng nhau của tam giác? Vẽ hình minh họa cho từng trường hợp?
Câu 2: Phát biều những trường hợp bằng nhau của tam giác vuông? Vẽ hình minh họa cho từng trường hợp?
Câu 3: Phát biều định lí một đường thẳng vuông góc với mọt trong hai tuyến đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh họa?
Câu 4: Phát biều định lí hai tuyến đường thẳng cùng vuông góc với một đường thẳng? Ghi giả thiết kết luận? Vẽ hình minh họa?
Câu 5: Phát biều định lí ba đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh?
Câu 6: Các em tự tìm hiểu những t/c, định lí nào có liêu quan đến những trường hợp bằng nhau của tam giác? Kể tên?
II. Bài tập:
Bài 1: Cho tam giác ABC có
. Gọi M là trung điểm của BC. Tính những góc của tam giác AMB và tam giác AMC.Bài 2. Cho tam giác ABC có D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Biết
a) Chứng minh
b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của
c) Giả sử
. Tính những góc còn lai của tam giác DAE.Bài 3. Cho tam giác ABC vuông ở A. TRên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh DABC = DABD
b) Trên tia đối của tia AB, lấy điểm M. Chứng minh DMBD = D MBC.
Bài 4. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a) D AOI = D BOI.
b) AB vuông góc OI..
Bài 5. Cho
có 
. Kẻ tia phân giác 
của 
( D thuộc BC). Trên canh AC lấy điểm E sao cho A E=A B, trên tia A B lấy điểm F sao cho A F=A C. Chứng minh rằng:c) FDE thẳng hàng.
Bài 6. Cho góc nhọn
. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA=OB ;OC=OD. (A nằm giữa O và C; B Nằm giữa O và D).a) Chứng minh
b) So sánh 2 góc
và 
Bài 7. Cho DABC vuông ở A. TRên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh DABC = DABD
b) Trên tia đối của tia AB, lấy điểm M. Chứng minh DMBD = D MBC.
Bài 8. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a) D AOI = D BOI.
b) AB vuông góc OI.
Bài 9. Cho DABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.
a) Chứng minh AC // BE.
b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.
Bài 10. Cho vuông tai
a) Tính
b) Trên canh
, lấy điểm D sao cho BD=BA. Tia phân giác của góc B cắt cạnh AC tai E. Chứng minh 
c) Qua c, vẽ đường thẳng vuông góc với BE tại H, CH cắt AB tại F. Chứng minh
d) Chứng minh
và ba điểm D, E, F thẳng hàngBài 11. Cho , có
và M là trung điểm của BCa) Chứng minh
b) Qua A vẽ
Chứng minh 
và a / / B Cc) Qua C, vẽ b/ / AM. Goi N là giao điểm của hai tuyến đường thẳng a và b. Chứng minh
d) Gọi I là trung điểm của đoạn AC. Chứng minh I là trung điểm của đoạn MN
Bài 12. Cho , gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh rằng:
a)
b) AB = AC và AB//CD
c)
d) Trên những đoạn thẳng AB, CD lần lượt lấy những điểm E, F sao cho AE=AF. Chứng minh E, M, F thẳng hàng
Bài 13. Cho vuông tai
. Tia phân giác của 
cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE= BA. Vẽ 
tại H. Chứng minh rằng:a)
và 
b)
c) Trên tia
lấy điểm K sao cho DK=AH. Gọi M là trung điểm của đoan DHChứng minh A, M, K thẳng hàng
Bài 14. Cho , Gọi D là trung điểm của AB. Qua D kẻ đường thẳng song song với BC cắt AC tại E, qua E kẻ đường thẳng song song với AB cắt BC tại F. Chứng minh rằng:
a) AD = EF
b) AE = EC
Bài 15. Cho . Gọi M, N thứ tự là trung điểm của AB và AC. Lấy P sao cho N là trung điểm của MP. Chứng minh rằng:
b)
, Từ đó suy ra 
Bài 16. Cho
nhọn. Lấy A trên Ox, B trên Oy sao cho OA=OB. Qua A kẻ đưởng thẳng vuông góc với 
cắt Oy tại M, qua B kẻ đt vuông góc Oy cắt Ox tại N. Gọi H là giao điểm của AM và BN, I là trung điểm của MN. Chứng minh rằng:a) ON = OM
b) Ba điểm O, H, I thẳng hàng
Bài 17. Cho có
, kẻ 
là những tia phân giác của 
cắt 
tại Ia) Tính
b) Kẻ IF là những tia phân giác của
. Chứng minh rằng:Bài 18. Cho nhọn. Vẽ về phía ngoài những đoạn thẳng
và 
Kẻ
, EK vuông góc với đường thẳng 
. Chứng minh rằng:Bài 19. Cho . Trên cạnh AB lấy M và N sao cho AM = BN. Qua M và N kẻ những đt song song với BC, cắt AC thứ tự tại D và E. Cmr:
Bài 20 :
Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD = AB; AE = AC
a) Chứng minh BE = DC
b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 21.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 22
Cho tam giác ABC có góc A =350 . Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.
a) Chứng minh ΔAHB = ΔDBH.
b) Chứng minh AB//HD.
c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.
