Thủ Thuật về Cho tam giác abc có ab = 4 ac = 3 và bc = 6 tính độ dài trung tuyến kẻ từ c của tam giác abc 2022
Hoàng Thị Hương đang tìm kiếm từ khóa Cho tam giác abc có ab = 4 ac = 3 và bc = 6 tính độ dài trung tuyến kẻ từ c của tam giác abc được Update vào lúc : 2022-05-09 01:30:36 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Sau đây THPT Sóc Trăng sẽ chia sẻ đến những bạn công thức tính độ dài trung tuyến trong tam giác cực hay và những dạng toán thương gặp. Hãy chia sẻ để nắm chắc hơn phần kiến thức và kỹ năng Hình học 12 vô cùng quan trọng này bạn nhé !
I. LÝ THUYẾT VỀ ĐƯỜNG TRUNG TUYẾN TRONG TAM GIÁC
1. Đường trung tuyến là gì? Đường trung tuyến trong tam giác là gì?
Bạn đang xem: Công thức tính độ dài trung tuyến trong tam giác & những dạng bài tập
Đường trung tuyến của một đoạn thẳng là một trong đường thẳng đi qua trung điểm của đường thẳng đó
Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới những cạnh đối diện nó. Mỗi tam giác có 3 đường trung tuyến.
2. Tính chất của đường trung tuyến trong tam giác
Trong tam giác thường, vuông, cân đều có tính chất của đường trung tuyến rất khác nhau.
Đường trung tuyến trong tam giác thường gồm 3 tính chất như sau:
- 3 đường trung tuyến trong tam giác cùng đi qua 1 điểm, điểm đó cách đỉnh tam giác một khoảng chừng bằng độ dài của đường trung tuyến đi qua đỉnh đó.
Giao điểm của 3 đường trung tuyến được gọi là trọng tâm
Vị trí trọng tâm trong tam giác: Trọng tâm của một tam giác cách mỗi đỉnh 1 khoảng chừng bằng độ dài đường trung tuyến đi qua đỉnh đó.
Tính chất đường trung tuyến của tam giác vuông:
Tam giác vuông là một trường hợp đặc biệt của tam giác, trong đó, tam giác sẽ có một góc có độ lớn là 90 độ, và hai cạnh tạo nên góc này vuông góc với nhau.
– Do đó, đường trung tuyến của tam giác vuông sẽ có đầy đủ những tính chất của một đường trung tuyến tam giác.
Định lý 1: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Định lý 2: Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
Tính chất đường trung tuyến của tam giác đều, tam giác cân
- Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đấy, và chia tam giác thành 2 tam giác bằng nhau
II. CÔNG THỨC TÍNH ĐỘ DÀI ĐƯỜNG TRUNG TUYẾN TRONG TAM GIÁC
Công thức:
Công thức tính độ dài đường trung tuyến của cạnh bất kỳ bằng căn bậc 2 của một phần hai tổng bình phương hai cạnh kề trừ một phần tư bình phương cạnh đối.
Trong số đó: a, b ,c lần lượt là những cạnh trong tam giác
ma, mb, mc lần lượt là những đường trung tuyến trong tam giác
Ví dụ minh họa:
Ví dụ 1:
Cho tam giác ABC, có BC = a, CA = b và AB = c. Chứng minh rằng nếu b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau.
Lời giải:
Gọi D và E lần lượt là trung điểm của AB và AC, G là trọng tâm tam giác ABC.
Đặt BE = mb, CD = mc
Áp dụng công thức trung tuyến trong tam giác ABC ta có:
Vậy b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau. (đpcm)
Ví dụ 2: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài những đường trung tuyến của tam giác ABC.
Lời giải:
Gọi độ dài trung tuyến từ những đỉnh A, B, C của tam giác ABC lần lượt là ma; mb; mc.
Áp dụng công thức trung tuyến ta có:
Vì độ dài những đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương, do đó:
III. BÀI TẬP VẬN DỤNG
Bài 1: Cho tam giác ABC cân tại A, hai tuyến đường trung tuyến BD và CE cắt nhau tại G. Kéo dài AG cắt BC tại H.
a. So sánh tam giác AHB và tam giác AHC.
b. Gọi I và K lần lượt là trung điểm của GA và GC. Chứng minh rằng AK, BD, CI đồng quy.
Lời giải:
a. Ta có BD là đường trung tuyến của tam giác ABC
CE là đường trung tuyến của tam giác ABC
Vậy G là trọng tâm tam giác ABC
Mà AH đi qua G nên AH là đường trung tuyến của tam giác ABC
HB = HC
Xét hai tam giác AHB và tam giác AHC có:
AB = AC (tam giác ABC cân tại A)
AH chung
HB = HC
⇒ ΔAHB = ΔAHC (c – c – c)
b. Ta có IA = IG nên CI là đường trung tuyến của tam giác AGC (1)
Ta lại sở hữu KG = KC nên AK là đường trung tuyến của tam giác AGC (2)
DG là đường trung tuyến của tam giác AGC (3)
Từ (1), (2), (3) suy ra 3 đường trung tuyến CI, AK, DG đồng quy tại I
Bài 2: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài những đường trung tuyến của tam giác ABC.
Lời giải:
Gọi độ dài trung tuyến từ những đỉnh A, B, C của tam giác ABC lần lượt là ma; mb; mc.
Áp dụng công thức trung tuyến ta có:
Vì độ dài những đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương, do đó:
Bài 3: Cho tam giác MNP cân tại M, biết MN = MP = 8cm, NP = 7cm. Kẻ đường tuyến MI. Chứng minh MI ﬩ NP
Lời giải:
Ta có MI là đường trung tuyến của ∆MNP nên IN = IP
Mặt khác ∆MNP là tam giác cân tại M
=> MI vừa là đường trung tuyến vừa là đường cao
=> MI ﬩ NP
Bài 4: Cho tam giác ABC có AB = AC, gọi K là giao điểm của hai tuyến đường trung tuyến BM và CN. Chứng minh rằng:
a. Tam giác BNC và tam giác CMB bằng nhau
b. KB = KC
c. BC < 4KM
Lời giải:
a. Ta có: AB = AC (gt)
⇒ BN = CM
Xét ΔBCN và ΔCBM có:
BC là cạnh chung
BN = CM
Nên tam giác KBC cân tại A
Suy ra KB = KC
c. Xét ΔABC có:
NA = NB (CN là đường trung tuyến)
MA = MC (MB là đường trung tuyến)
Suy ra NM là đường trung bình của tam giác ABC
Xét tam giác NKM có:
NM < NK + KM (bất đẳng thức Cauchy trong tam giác)
NK = CN – CK
⇒ BC/2 < CN – CK + KM (1)
ΔBNC = ΔCMB ⇒ CN = BM (2)
Tam giác KBC cân tai K ⇒ CK = BK (3)
Từ (1), (2), (3) ⇒ BC/2 < BM – BK + KM
⇒ BC/2 < 2KM
⇒ BC < 4KM
Bài 5: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên cạnh AC lấy điểm E sao cho AE = 1/3AC. Tia BE cắt CD ở M. Chứng minh :
a) M là trung điểm của CD
b) AM =
BC.
Hướng dẫn giải
a. Xét tam giác BDC có AB = AD suy ra AC là đường trung tuyến tam giác BCD
Mặt khác
Suy ra E là trọng tâm tam giác BCD
M là giao của BE và CD
Vậy BM là trung tuyến tam giác BCD
Vậy M là trung điểm của CD
b. A là trung điểm của BD
M là trung điểm của DC
Suy ra AM là đường trung bình của tam giác BDC
Suy ra AM = 1/2 BC
Bài 6: Cho tam giác ABC vuông ở A, có AB = 18cm, AC = 24cm. Tính tổng những khoảng chừng cách từ trọng tâm G của tam giác đến những đỉnh của tam giác.
Hướng dẫn giải
Gọi AD, CE, BF lần lượt là những đường trung tuyến nối từ đỉnh A, C, B của tam giác ABC
Dễ dàng suy ra AE = EB = 9cm, AF = FC = 12cm
Ta có tam giác ABC vuông tại A, áp dụng định lý Pitago ta có:
BC2 = AB2 + AC2 ⇒ BC2 = 182 + 242 = 900 ⇒ BC = 30cm
Ta có ABC vuông mà D là trung điểm cạnh huyền nên AD = BD = DC = 15cm
Suy ra: AG = 2/3 AD = 10cm
Xét tam giác AEC vuông tại A, áp dụng định lý Pitago ta có:
EC2 = AE2 + AC2 ⇒ EC2 = 92 + 242 = 657 ⇒ EC = 3√73 cm ⇒ CG = 2/3 EC = 2√73 cm
Tương tự ta xét tam giác AFB vuông tại A, áp dụng định lý Pitago ta có:
BF2 = AB2 + AF2 ⇒BF2 = 182 + 122 = 468 ⇒ BF = 6√13 cm ⇒ BG = 2/3 BF = 4√13 cm
Tổng những khoảng chừng cách từ trọng tâm G của tam giác đến những đỉnh của tam giác là:
AG + BG + CG = 10 + 4√13 + 2√73 (cm)
Bài 7: Gọi S = ma2 + mb2 + mc2 là tổng bình phương độ dài ba đường trung tuyến của tam giác ABC. Khẳng định nào sau đây là đúng? (cho BC = a, CA = b, AB = c)
Lời giải:
Áp dụng công thức trung tuyến trong tam giác ABC ta có:
Đáp án A
Bài 8: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến
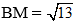. Độ dài AC là:
Hướng dẫn giải:
BM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có:
Đáp án B
Trên đây THPT Sóc Trăng đã ra mắt đến quý thầy cô và những bạn công thức tính độ dài trung tuyến trong tam giác cực hay và những dạng toán thương gặp. Hi vọng, đây là nguồn tư liệu thiết yếu giúp những bạn dạy và học tốt hơn. Xem thêm phương pháp tính tọa độ trọng tâm tam giác nữa bạn nhé !
Đăng bởi: THPT Sóc Trăng
