Kinh Nghiệm về Đồng biến trên từng khoảng chừng xác định là gì Chi Tiết
HỌ VÀ TÊN NỮ đang tìm kiếm từ khóa Đồng biến trên từng khoảng chừng xác định là gì được Cập Nhật vào lúc : 2022-07-19 20:46:03 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.A. 2
B. 0
C. 4
D. 1
Lời giải:
Chọn D
Xét hàm số
f(x) = x5 – 5x2 + 5(m – 1)x – 8
TH1: f(x) = 0 có nghiệm x0 ∊ (-∞;1) thì hàm số y = |f(x)| không thể nghịch biến trên khoảng chừng (-∞;1).
TH2: f(x) = 0 không còn nghiệm x0 ∊ (-∞;1)
Ta có: f’(x) = 5x4 – 10x + 5(m – 1)
Khi đó y = |x5 – 5x2 + 5(m – 1)x – 8| = |f(x)| =

Nên
Hàm số nghịch biến trên (-∞;1) khi và chỉ khi y’ ≤ 0 với ∀ x ∊ (-∞;1)

Mà m ∊ ℤ nên m = 3
Ví dụ 2. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |2x3 – mx + 1| đồng biến trên khoảng chừng (1; +∞)?A. 2
B. 6
C. 3
D. 4
Lời giải:
Chọn C
Xét hàm số
f(x) = 2x3 – mx + 1
TH1: f(x) = 0 có nghiệm x0 ∊ (1;+∞) thì hàm số y = |f(x)| không thể nghịch biến trên khoảng chừng (1;+∞).
TH2: f(x) = 0 không còn nghiệm x0 ∊ (1;+∞)
Ta có: f’(x) = 6x2 – m
Khi đó y = |2x3 – mx + 1| = |f(x)| =
Nên
Hàm số nghịch biến trên khoảng chừng (1;+∞) khi và chỉ khi y’ ≥ 0 với ∀ x ∊ (1;+∞)
⇒ m ∊ 1; 2; 3
Ví dụ 3. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số y = |3x4 – 4x3 – 12x2 + m| nghịch biến trên khoảng chừng (-∞; -1)?A. 6
B. 4
C. 3
D. 5
Lời giải
Chọn D
Xét hàm số f(x) = 3x4 – 4x3 – 12x2 + m ⇒ f’(x) = 12x3 – 12x2 – 24x = 12x (x2 – x – 2)
⇒ f’(x) = 0
BBT:
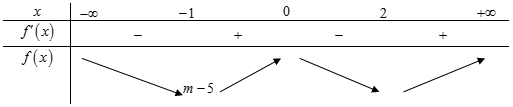
Nhận thấy: Hàm số y = |f(x)| nghịch biến trên khoảng chừng (-∞; -1) ⇔ m – 5 > 0 ⇔ m ≥ 5.
Lại do ⇒ m ∊ 5; 6; 7; 8; 9
Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Loại 2: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số dạng phân thức hữu tỉ đồng biến, nghịch biến trên tập D cho trước.Ví dụ 1. Tính tổng S tất cả những giá trị nguyên của tham số m trong đoạn [-10; 10] để hàm số đồng biến trên (1; +∞).A. S = 55
B. S = 54
C. S = 3
D. S = 5
Lời giải
Chọn B.
Xét hàm số với x ≠ -m – 2, có
Hàm số đồng biến (1; +∞) khi xảy ra một trong hai trường hợp sau:
TH1:
TH2:
Vậy m ∊ (1; +∞), lại do suy ra m ∊ 2; 3; 4; 5; 6; 7; 8; 9; 10
Vậy S = 54
Ví dụ 2. Tìm m để hàm số đồng biến trên (1;+∞)A.
B.
C.
D.
Lời giải
Chọn B
Đặt . ĐK: x ≠ -m
Khi đó
Để hàm số đồng biến trên (1;+∞) ⇔
 hoặc
hoặc Ta có
Vậy ⅓ < m ≤ 1
Ví dụ 3. Có bao nhiêu số nguyên của tham số m để hàm số đồng biến trên [3; +∞)?A. 4
B. 5
C. Vô số
D. 6
Lời giải
Chọn A
Tập xác định: D = ℝ 1
Xét hàm số
Có
Khi đó
Hàm số đồng biến trên [3; +∞) ⇔ y’ ≥ 0, ∀ x ∊ [3; +∞)
Vì m ∊ ℤ ⇒ m ∊ -2; -1; 0; 1
Vậy có 4 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Loại 3: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số chứa căn đồng biến, nghịch biến trên tập D cho trước.Ví dụ 1. Cho hàm số . Có bao nhiêu giá trị m nguyên để hàm số nghịch biến trên (0;1).A. 4
B. 2
C. 3
D. 5
Lời giải
Chọn A
Đặt
Ta có
Do hàm số liên tục tại x = 0; x = 1 nên để hàm số nghịch biến trên (0;1) ta xét 2 trường hợp sau:
Trường hợp 1:
Trường hợp 2:

 (vô nghiệm)
(vô nghiệm)Do m nguyên nên m nhận những giá trị sau -3; -2; -1; 0
Ví dụ 2. Có bao nhiêu giá trị nguyên của tham số m ∊ (-5; 5) để hàm số nghịch biến trên (2; 3)?A. 2
B. 3
C. 5
D. 9
Lời giải
Chọn B
Xét hàm số
Ta có
Cho f’(x) = 0
Ta thấy f’(x) < 0, ∀ x ∊ (2; 3) nên hàm số f(x) nghịch biến trên (2; 3)
Để nghịch biến trên (2; 3) thì
f(3) ≥ 0
Do m ∊ (-5; 5) nên m = -2; -3; -4
Ví dụ 3. Có bao nhiêu giá trị nguyên của tham số m ∊ [0; 10] để hàm số đồng biến trên khoảng chừng (1;+∞)?A. 11
B. 10
C. 12
D. 9
Lời giải
Chọn A
Tập xác định D = ℝ
Xét hàm số
Hàm số đồng biến trên khoảng chừng (1;+∞)
TH1:
f’(x) ≥ 0, ∀ x ∊ (1;+∞)
Đặt t = x – 1, t > 0
Xét
Bảng biến thiên:
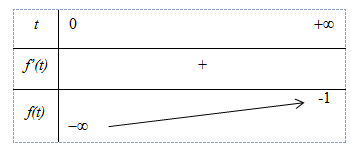
Từ BBT ta có
TH2:
f’(x) ≤ 0, ∀ x ∊ (1;+∞)

Đặt t = x – 1, t > 0
Mà nên với mỗi giá trị của m luôn có mức giá trị của t dương đủ nhỏ để VT của (*) to hơn 0.
Suy ra không còn mức giá trị nào của m để TH2 thỏa mãn.
Vậy có 11 giá trị nguyên của m thỏa mãn là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
Loại 4: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số lượng giác đồng biến, nghịch biến trên tập D cho trước.Ví dụ 1. Có bao nhiêu giá trị m nguyên để hàm số y = |f(x)| = |x3 – 3x2 +3(mét vuông + 5) x + (12 – 3m2) cosx| đồng biến trên (0; π)A. 3
B. 5
C. 4
D. Vô số
Lời giải
Chọn B
Đặt h(x) = x3 – 3x2 + 3(mét vuông + 5) x + (12 – 3m2) cosx.
Ta có h’(x) = 3x2 – 6x + 3(mét vuông + 5) – (12 – 3m2) sinx.
⇔ h’(x) = 3(x – 1)2 + 12(1 – sinx) + 3m2(1 + sinx) ≥ 0, ∀ x ∊ (0; π)
Vậy hàm số h(x) luôn đồng biến trên (0; π).
Để y = f(x) đồng biến trên (0; π). Thì h(0) ≥ 0 ⇔ (12 – 3m2) ≥ 0 ⇔ m ∊ [-2; 2]
Kết luận: có 5 giá trị m nguyên thỏa mãn.
Ví dụ 2. Các giá trị của tham số m để hàm số y = |sinx – cosx + m| đồng biến trên khoảng chừng là.A.
B.
C. m > 1
D. m ≥ 1
Lời giải
Chọn B
Xét hàm số f(x) = sinx – cosx + m =

Khi đó y = |sinx – cosx + m| = |f(x)| = . Nên
Hàm số y = |sinx – cosx + m| đồng biến trên khoảng chừng ⇔ y’ ≥ 0, ∀ x ∊
Với
Nên (1) ⇔ f(x) > 0, ∀ x ∊
Ví dụ 3. Cho hàm số y = |sin3x – m.sinx + 1|. Gọi S là tập hợp tất cả những số tự nhiên m sao cho hàm số đồng biến trên . Tính số phần tử của S .A. 1
B. 2
C. 3
D. 0
Lời giải
Chọn A
Trên khoảng chừng , hàm số y = sinx đồng biến
Đặt t = sin x, x ∊ ⇒ t ∊ (0;1)
Khi đó hàm số y = |sin3x – m.sinx + 1| đồng biến trên khoảng chừng khi và chỉ khi
y = g(t) = |t3 – mt + 1| đồng biến trên (0;1)
Xét hàm số y = f(t) = t3 – mt + 1 trên khoảng chừng (0;1) có f’(t) = 3t2 – m.
+) Khi m = 0
f’(t) = 3t2 > 0, ∀ t ⇒ y = f(t) = t3 + 1 đồng biến trên (0;1) và đồng thời y = f(t) = t3 + 1 cắt trục hoành tại điểm duy nhất t = -1
⇒ y = g(t) = |t3 – mt + 1| đồng biến trên (0;1) ⇒ m = 0 thỏa mãn
+) Khi m > 0
f’(t) = 0 có 2 nghiệm phân biệt
Hàm số y = f(t) = t3 – mt + 1 đồng biến trên những khoảng chừng và
TH1: ⇔ 0 < m < 3
Hàm số y = f(t) = t3 – mt + 1 nghịch biến trên khoảng chừng và đồng biến trên khoảng chừng
⇒ Không có mức giá trị của m để y = g(t) = |t3 – mt + 1| đồng biến trên (0;1)
TH2: ⇔ m ≥ 3
Để y = g(t) = |t3 – mt + 1| đồng biến trên (0;1) thì t3 – mt + 1 ≤ 0, ∀ x ∊ (0;1)
⇔ mt ≤ t3 + 1, ∀ x ∊ (0;1)
⇒ Không có mức giá trị của m thỏa mãn
Vậy chỉ có mức giá trị m = 0 thỏa mãn
Ví dụ 4. Có bao nhiêu giá trị nguyên của m thuộc [-5;5] để hàm số y = |cos3x – 3m2cosx| nghịch biến trên .A. 1
B. 11
C. 5
D. 6
Lời giải
Chọn B
Đặt t = cos x, vì x ∊ ⇒ t ∊ (0;1)
Vì t =cos x là hàm số nghịch biến trên nên yêu cầu bài toán trở thành tìm m nguyên thuộc [-5;5] để hàm số y = |t3 – 3m2t| đồng biến trên (0;1).
Xét f(t) = t3 – 3m2t, t ∊ (0;1) ⇒ f’(t) = 3t2 – 3m2
TH1: Nếu m = 0 ⇒ f’(t) > 0, ∀ t ∊ (0;1) ⇒ f(t) luôn đồng biến trên (0;1)
Mà f (0) = 0 ⇒ y = |f(t)| luôn đồng biến trên (0; +∞)
⇒ y = |f(t)| luôn đồng biến trên (0;1)
Do đó m = 0 thỏa mãn bài toán (1)
TH2: m ≠ 0 ⇒ f’(t) = 0
*) Với m > 0 , ta có BBT sau:
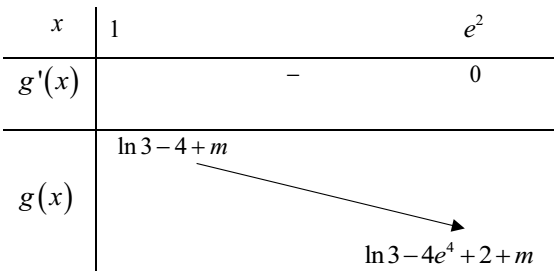
Từ BBT suy ra hàm số y = |f(t)| luôn đồng biến trên (0; m)
YCBT tương đương (0;1) ⊂ (0; m) ⇔ m ≥ 1 (2)
*) Với m < 0 , ta có BBT sau:
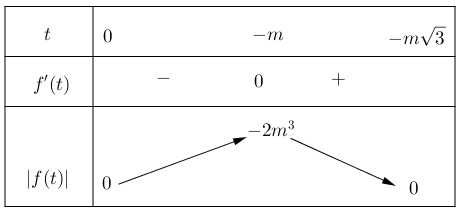
Từ BBT suy ra hàm số y = |f(t)| luôn đồng biến trên (0; -m)
YCBT tương đương (0;1) ⊂ (0; -m) ⇔ m ≤ -1 (3)
Từ (1), (2) và (3) vậy có 11 giá trị nguyên của m thỏa mãn bài toán.
Loại 5: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số mũ đồng biến, nghịch biến trên tập D cho trước.Ví dụ 1. Có bao nhiêu giá trị nguyên dương của m để y = |9x + 3x – m + 1| đồng biến trên đoạn [0;1]A. 1
B. 4
C. 3
D. 6
Lời giải
Chọn C
Đặt 3x = t ⇒ t ∊ [1;3] vì t ∊ [0;1]
⇒ t = |t2 + t – m + 1| =
Để hàm số đồng biến trên đoạn t ∊ [1;3] thì
Với mọi giá trị của t ∊ [1;3] thì 2t + 1 > 0 nên
Để y’ ≥ 0, ∀ t ∊ [1;3] thì t2 + t – m + 1 ≥ 0, ∀ t ∊ [1;3]
⇒ m – 1 ≤ t2 + t = g(t) , ∀ t ∊ [1;3]

Vậy có 3 giá trị nguyên 1; 2; 3 thỏa mãn yêu cầu bài toán.
Ví dụ 2. Có bao nhiêu giá trị m nguyên dương và nhỏ hơn 2022 để hàm số y = |4x + m.2x+1 + m + 2| đồng biến trên khoảng chừng (0;1)?A. 2022
B. 2022
C. 2
D. 3
Lời giải
Chọn A
Xét hàm số f(x) = 4x + m.2x+1 + m + 2 (1) trên khoảng chừng (0;1)
Đặt t = 2x ⇒ t ∊ (1;2)
Hàm số (1) trở thành h(t) = t2 – 2mt + m + 2 trên khoảng chừng (1;2).
Suy ra h’(t) = 2t – 2m
Ta có y = |f(x)| đồng biến trên khoảng chừng (0;1)

Vì hàm số t = 2x đồng biến trên khoảng chừng (0;1)
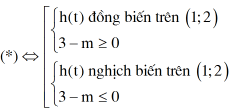
Do đó,

Vậy có 2022 số nguyên dương nhỏ hơn 2022 thỏa ycbt.
Ví dụ 3. Cho hàm số (1). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số nghịch biến trên khoảng chừng (2;4)?A. 234
B. Vô số
C. 40
D. Không tồn tại m
Lời giải
Chọn C
Đặt
Ta có ⇒ t ∊ (e2; e3), đồng thời x và t sẽ ngược chiều biến thiên.
Khi đó hàm số trở thành y = |t2 + 3t – 2m + 5| = (2)
Ta có:
Hàm số (1) nghịch biến trên khoảng chừng (2;3) ⇔ hàm số (2) đồng biến trên khoảng chừng (e2; e3)
∀ x ∊ (e2; e3)
⇔ t2 + 3t – 2m + 5 > 0 ∀ x ∊ (e2; e3)
∀ x ∊ (e2; e3)
Có ∀ x ∊ (e2; e3)
Với điều kiện m là số nguyên dương ta tìm được 40 giá trị của m.
Ví dụ 4. Có bao nhiêu giá trị nguyên dương m ∊ (-2022; 2022), để hàm số y = |e-x2 + ex2 – m| nghịch biến trên (1;e)?A. 401
B. 0
C. 2022
D. 2022
Lời giải
Chọn A
Đặt f(x) = e-x2 + ex2 – m ⇒ f’(x) = -2xe-x2 + 2ex2
Ta có y = |f (x)| =
Yêu cầu bài toán ⇔ y’ ≤ 0, ∀ x ∊ (1;e) (*)
Vì x ∊ (1;e) nên -2xe-x2 + 2ex2 = , ∀ x ∊ (1;e)
Khi đó, (*) ⇔ f(x) ≤ 0, ∀ x ∊ (1;e)
⇔ e-x2 + ex2 – m ≤ 0, ∀ x ∊ (1;e)
⇔ e-x2 + ex2 ≤ m, ∀ x ∊ (1;e)
Ta có mức giá trị lớn số 1 của hàm số y = e-x2 + ex2 ∀ x ∊ (1;e) là e-x2 + ex2
Nên m ≥ e-x2 + ex2 ≈ 1618,18
Vậy có 401 giá trị nguyên dương m thỏa mãn.
Loại 6: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số logarit đồng biến, nghịch biến trên tập D cho trước.Ví dụ 1. Có bao nhiêu giá trị nguyên thuộc khoảng chừng (-100; 100) của tham số m để hàm số y = |ln3x – 4x2 + m| đồng biến trên đoạn [1;e2]?A. 101
B. 102
C. 103
D. 100
Lời giải
Chọn B
y = |ln3x – 4x2 + m|. Điều kiện x > 0
Xét hàm số g(x) = ln3x – 4x2 + m trên [1;e2]
⇒ g(x) nghịch biến trên [1;e2]

⇒ Hàm số y = |g(x)| = |ln3x – 4x2 + m| đồng biến trên đoạn [1;e2]
⇔ ln3 – 4 + m ≤ 0 ⇔ m ≤ 4 – ln3
Mà m nguyên thuộc khoảng chừng (-100; 100) nên m ∊ -99; -98;…; -1; 0; 1; 2
Vậy có 102 giá trị m nguyên thỏa mãn yêu cầu bài toán.
Ví dụ 2. Có bao nhiêu số nguyên m < 2022 để hàm số y = |ln(mx) – x + 2| nghịch biến trên (1;4)?A. 2022
B. 2022
C. 1
D. Vô số.
Lời giải
Chọn A
Xét f(x) = ln(mx) – x + 2.
Dễ thấy ∀ x ∊ (1;4): mx > 0 ⇔ m > 0
Khi đó
Do đó f(x) luôn nghịch biến trên (1;4)
Yêu cầu bài tóan tương đương với f(4) ≥ 0 ⇔ ln(4m) – 2 ≥ 0
Vậy m ∊ [2; 2019] có 2022 số nguyên thỏa mãn.
Ví dụ 3. Có bao nhiêu số nguyên m thuộc (-2022; 2022) để hàm số y = |ln(x2 + 2x – m) – 2mx2 – 1| luôn đồng biến trên (0;10)?A. 4038
B. 2022
C. 2022
D. 2022
Lời giải
Chọn C
Ta xét hàm số f(x) = ln(x2 + 2x – m) – 2mx2 – 1 trên (0;10)
Điều kiện hàm số nghĩa là x2 + 2x – m > 0, ∀ x ∊ (0;10)
⇔ x2 + 2x > m, ∀ x ∊ (0;10) (1)
Ta lại sở hữu x2 + 2x = x.(x + 2) > 0 với ∀ x ∊ (0;10) nên điều kiện (1) cho ta m ≤ 0 (2)
Đạo hàm do m ≤ 0 và x ∊ (0;10) nên
Suy ra f’(x) > 0 hàm số đồng biến trên (0;10).
Từ đó để hàm số y = |ln(x2 + 2x – m) – 2mx2 – 1| = |f(x)| đồng biến trên (0;10) điều kiện đủ là f(x) ≥ 0 với ∀ x ∊ (0;10) (3)
+) TH1: Xét m = 0
Khi đó f(x) = ln(x2 + 2x) – 1 có không thỏa mãn (3)
+) TH2: Xét m < 0
Do hàm số f(x) đồng biến nên ta chỉ việc f(0) ≥ 0 ⇔ ln(-m) – 1 ≥ 0 ⇔ -m ≥ e ⇔ m ≤ -e
Từ đó ta được:
⇔ m ∊ -2022; -2022; -2022;…; -3 có 2022 giá trị m thỏa mãn bài toán.
Ví dụ 4. Có bao nhiêu số nguyên của tham số m trong đoạn [-3;3] để hàm số y = |ln(x3 + mx + 2)| đồng biến trên nửa khoảng chừng [1;3)?A. 7
B. 4
C. 6
D. 5
Lời giải
Chọn C
Điều kiện xác định: x3 + mx + 2 > 0
Xét hàm số f(x) = ln(x3 + mx + 2)
Ta có:
Hàm số đồng biến trên nửa khoảng chừng [1;3)
Trường hợp 1:
Trường hợp 2:
Từ hai trường hợp trên suy ra m ≥ -2
Mà m ∊ [-3;3] ⇒ m ∊ -2; -1; 0; 1; 2; 3
Vậy có 6 số nguyên m thỏa mãn YCBT.
