Mẹo Hướng dẫn Hình vuông có phải đa giác đều không 2022
Khoa Minh Hoàng đang tìm kiếm từ khóa Hình vuông có phải đa giác đều không được Update vào lúc : 2022-07-29 02:40:09 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
LUYỆN TẬP ĐA GIÁC – ĐA GIÁC ĐỀU
(CÓ ĐÁP ÁN)
Bài 1. Hãy vẽ một lục giác lồi và nêu cách nhận ra một đa giác lồi.
HD:
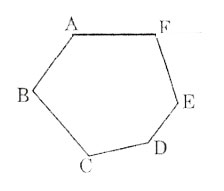
Cách nhận ra một đa giác lồi: Một đa giác lồi là một đa giác thỏa mãn 2 điều kiện sau:
– Các cạnh chỉ cắt nhau tại những đỉnh, nghĩa là không còn hai cạnh nào cắt nhau tại một điểm mà không phải là đỉnh. Một đagiác thỏa mãn điều kiện này là đa giác đơn.
– Đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa một cạnh tùy ý của nó. Một đa giác đơn thỏa mãn thêm điều kiện này là đa giác lồi.
Bài 2: Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:
a) Có tất cả những cạnh bằng nhau.
b) Có tất cả những góc bằng nhau.
Lời giải:
a) Hình thoi có tất cả những cạnh bằng nhau nhưng những góc hoàn toàn có thể không bằng nhau nên hình thoi không buộc phải là đa giác đều.
b) Hình chữ nhật có tất cả những góc bằng nhau nhưng những cạnh hoàn toàn có thể không bằng nhau nên hình chữ nhật không buộc phải là đa giác đều.
Bài 3 trang 115. Cho hình thoi ABCD có ∠A = 600 . Gọi E, F, G, H lần lượt là trung điểm của những cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
Lời giải:
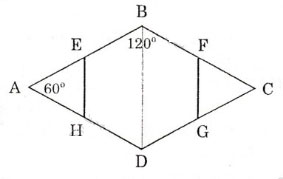
Vì ABCD là hình thoi, ∠A =600 Nên ∠B= 1200và ∠D = 1200
+ Ta có: AB = AD và AE = EB, AH = HD ⇒ AE = AH ⇒ ΔAEH cân tại A.
Mà ∠A =600 nên ΔAEH đều ⇒ ∠HEB = ∠EHD = 1200 (Góc ngoài của Δ đều AEH) và HE = AE = HD.
+ Tương tự: ΔFCG đều ⇒ ∠BFG = ∠FGD = 1200 và FG = FC = BF.
Vậy lục giác EBFGDH có EB = BF = FG = DG = HD = HE.
Và ∠HEB = ∠B = ∠BFG = ∠FGD = ∠D = ∠DHE (cùng bằng 1200)
Suy ra EBFGDH là một lúc giác đều.
Bài 4. Điền số thích hợp vào những ô trống trong bảng
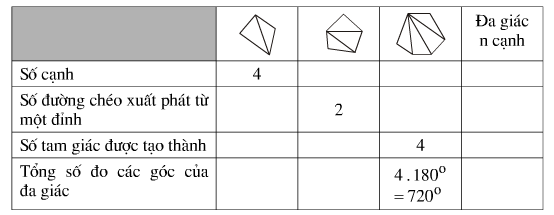
Lời giải:
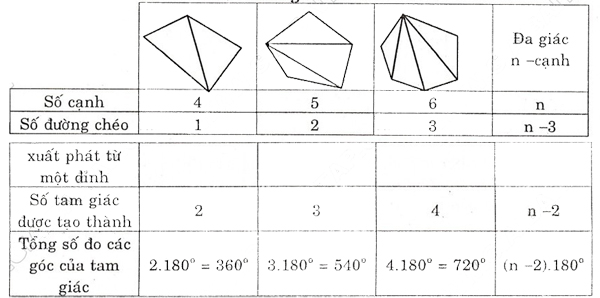
Bài 5. Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n- giác đều.
Lời giải:
Tổng số đo những góc của hình n giác bằng (n – 2).1800 (bằng tổng số đo những góc của số tam giác được tạo thành bởi những cạnh và những đường chéo xuất phát từ 1 đỉnh). Vậy số đo mỗi góc của n – đa giác đều là: (frac(n - 2).180^circ n)
Áp dụng công thức trên, ta có:
– Số đo mỗi góc của ngũ giác đều là (frac(5 - 2).180^circ 5 = 108^circ )
– Số đo mỗi góc của lục giác đều là (frac(6 - 2).180^circ 6 = 120^circ )
Bài 6. Trong những hình dưới đây hình nào là đa giác lồi? Vì sao?
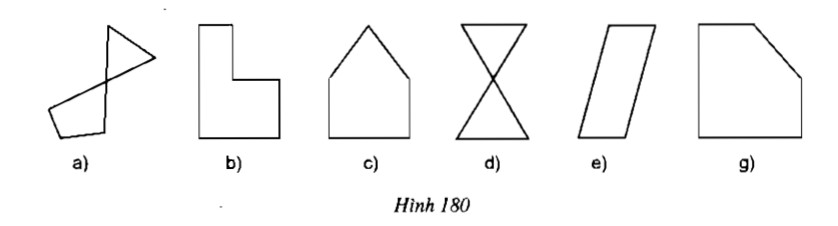
Lời giải:
Các hình c,e,g là những đa giác lồi vì đa giác nằm trên một nửa mặt phẳng với bờ chứa bất kì cạnh nào của đa giác.
Các hình a,b,d không phải là đa giác lồi vì đa giác nằm trên hai nửa mặt phẳng với bờ là đường thẳng chứa cạnh của đa giác.
Bài 7. Hãy vẽ một đa giác (lồi) mà những đỉnh là một điểm trong những điểm đã cho ở hình 181 (trên lưới kẻ ô vuông).
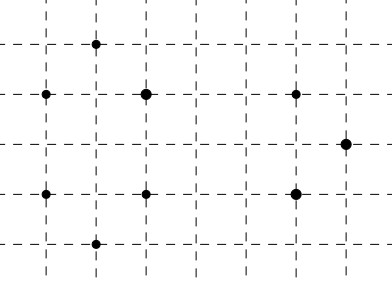
Giải:
Bài 8. Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.
Giải:
Áp dụng công thức tính số đo mỗi góc của đa giác đều có n cạnh bằng (fracleft( n - 2 right).180^0n)
- Đa giác đều 8 cạnh ⇒ n = 8, số đo mỗi góc là : (fracleft( 8 - 2 right).180^08 = 135^0)
- Đa giác đều 10 cạnh ⇒ n = 10, số đo mỗi góc là : (fracleft( 10 - 2 right).180^010 = 144^0)
- Đa giác đều 12 cạnh ⇒ n = 12, số đo mỗi góc là : (fracleft( 12 - 2 right).180^012 = 150^0)
Bài 9.
a. Vẽ hình và tính số đường chéo của ngũ giác, lục giác
b. Chứng minh rằng hình n – giác có tất cả (fracnleft( n - 3 right)2) đường chéo.
Giải:
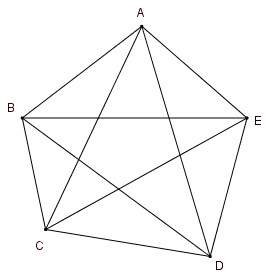
a. Từ mỗi đỉnh của ngũ giác vẽ được hai tuyến đường chéo. Ngũ giác có 5 đỉnh ta kẻ được 5.2 = 10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.
Từ mối đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả là 9 đường chéo.
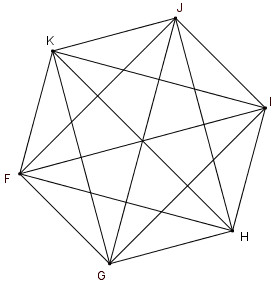
b. Từ mỗi đỉnh của n – giác nối với những đỉnh còn sót lại ta được n – 1 đoạn thẳng , trong đó có hai đoạn thẳng là cạnh của hình n – giác (hai đoạn thẳng nối với hai đỉnh kề nhau). Vậy qua mỗi đỉnh của n – giác vẽ được n – 3 đường chéo. Hình n – giác có n đỉnh kẻ được n(n – 3 ) đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy hình n – giác có tất cả (fracnleft( n - 3 right)2) đường chéo.
Bài 10. Chứng minh rằng tổng những góc ngoài của một đa giác (lồi) có số đo là 360°.
Giải:
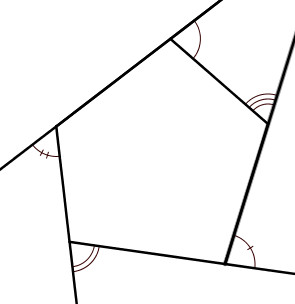
Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n – giác bằng 180°
Hình n – giác có n đỉnh nên tổng số đo những góc trong và góc ngoài của đa giác bằng n . 180°
Mặt khác ta biết tổng những góc trong của hình n – giác bằng (n – 2 ). 180°
Vậy tổng số đo những góc ngoài của hình n – giác là:
n . 180° - (n – 2) . 180° = n . 180° - n .180° +2. 180° = 360°
Bài 11. Đa giác nào có tổng số đo những góc (trong) bằng tổng số đo những góc ngoài ?
Giải:
Hình n – giác lồi có tổng số đo những góc trong bằng ( n – 2 ). 180° và tổng những góc ngoài bằng 360°
Đa giác lồi có tổng những góc trong bằng tổng những góc ngoài bằng 360°
⇒ (n – 2 ).180° = 360° ⇒ n = 4
Vậy tứ giác lồi có tổng những góc trong và góc ngoài bằng nhau.
Bài 12. Một đa giác (lồi) có nhiều nhất là bao nhiêu góc nhọn?
Giải:
Ta có: nếu góc của đa giác lồi là góc nhọn thì góc ngoài tương ứng là góc tù. Nếu đa giác lồi có 4 góc nhọn thì tổng những góc ngoài của đa giác to hơn 360°, xích míc định lý tổng những góc ngoài của đa giác lồi bằng 360°.
Vậy đa giác lồi có nhiều nhất là 3 góc nhọn.
Tất cả nội dung nội dung bài viết. Các em hãy xem thêm và tải file rõ ràng dưới đây:
>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học viên lớp 8 học tốt, hoàn trả học phí nếu học không hiệu suất cao.
Ta biết tam giác là hình gồm ba đoạn thẳng, tứ giác là hình gồm 4 đoạn thẳng và cứ thêm một đoạn thẳng, ta có một hình mới. Các hình đó có một tên gọi chung là đa giác.
Ta biết tam giác là hình gồm ba đoạn thẳng, tứ giác là hình gồm 4 đoạn thẳng và cứ thêm một đoạn thẳng, ta có một hình mới. Các hình đó có một tên gọi chung là đa giác.
1. Khái niệm đa giác
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
2. Định nghĩa đa giác đều
Đa giác đều là đa giác có tất cả những cạnh bằng nhau và tất cả những góc bằng nhau.
3. Góc trong đa giác
Tổng số đo những góc của đa giác n cạnh: (n – 2). 180°
Số đo một góc của đa giác đều n cạnh: [frac(n-2).180^0n]
4. Số đường chéo của đa giác n cạnh
[fracn(n-3)2]
Bài tập tương hỗ update:
1.Cho hình thoi ABCD có [widehatA=60^0].Gọi E,F,G,H lần lượt là trung điểm của những cạnh AB,BC,CD,DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
Lời giải rõ ràng
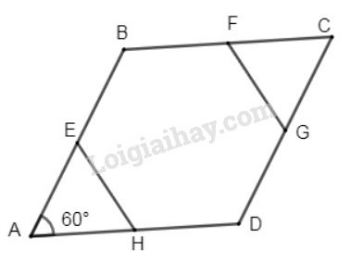
ABCD là hình thoi (gt) và [widehatA=60^0] (gt)
[widehatA+widehatABC=180^0](2 góc trong cùng phía bù nhau)
⇒[widehatABC=180^0=-widehatA=180^0-60^0=120^0]
⇒[widehatABC=widehatADC=120^0] (tính chất hình thoi)
ΔEAH là tam giác đều (vì tam giác cân có một góc [60^0]
⇒[widehatAEH=widehatAHE=60^0] (tính chất tam giác đều)
[widehatAEH+widehatHEB=180^0]
[widehatAHE+widehatEHD=180^0]
(kề bù)
⇒[widehatHEB=widehatEHD=180^0-60^0=120^0]
Tương tự: [widehatBFG=120^0,widehatFGD=120^0]
Vậy đa giác EBFGDH có tất cả những góc bằng nhau, mặt khác EBFGDH cũng luôn có thể có tất cả những cạnh bằng nhau ( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều (tín hiệu nhận ra lục giác đều)
2.Tại sao hình gồm năm đoạn thẳng AB, BC, CD, DE, EA ở hình 118 không phải là đa giác ?
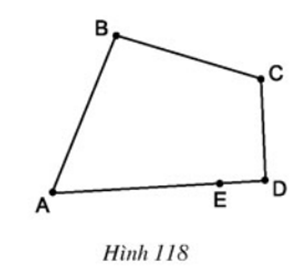
Lời giải
Hình 118 không phải là một đa giác vì DE và EA cùng nằm trên một đường thẳng
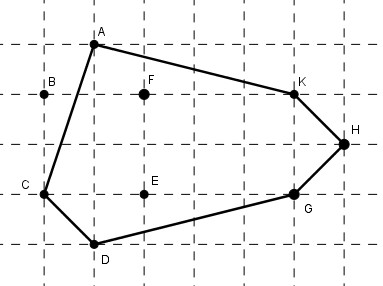
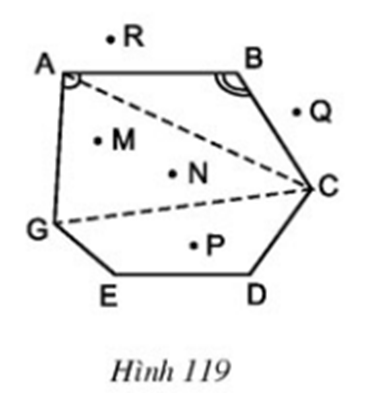
3. Toán 8 Tập 1 Bài 1 trang 114: Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong những câu sau:
Các đỉnh là những điểm: A, B, …
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …
Các cạnh là những đoạn thẳng: AB, BC, …
Các đường chéo là những đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …
Các góc là: ∠A , ∠B , …
Các điểm nằm trong đa giác (những điểm trong của đa giác) là: M, N, …
Các điểm nằm ngoài đa giác (những điểm ngoài của đa giác) là: Q., …
Lời giải
Các đỉnh là những điểm: A, B, C, D, E, G
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A
Các cạnh là những đoạn thẳng: AB, BC, CD, DE, EG, GA
Các đường chéo là những đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, AD, AE, BG, BE, BD, CE, DG
Các góc là: ∠A , ∠B , ∠C , ∠D , ∠E , ∠G
Các điểm nằm trong đa giác (những điểm trong của đa giác) là: M, N, P
Các điểm nằm ngoài đa giác (những điểm ngoài của đa giác) là: Q., R
Bài viết gợi ý: