Kinh Nghiệm Hướng dẫn Các bài toán về phương pháp chia tỉ lệ Chi Tiết
Hoàng Đại Thắng đang tìm kiếm từ khóa Các bài toán về phương pháp chia tỉ lệ được Cập Nhật vào lúc : 2022-08-22 14:36:03 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Một số bài toán.
Bài 1. Đầu năm học nhà trường mua cho khối 4 là 625 vở chia cho ba lớp. Biết 4A có 38 học viên, lớp 4B có 42 học viên, lớp 4C có 45 học viên, mỗi em được mua số vở bằng nhau. Hỏi mỗi lớp mua bao nhiêu vở
Phân tích: Từ số học viên 3 lớp ta tìm được tổng số học viên khối 4. Vì mỗi học viên được số vở bằng nhau nên ta tìm được số vở mỗi học viên được mua, từ đó ta đi tính số vở mỗi lớp được mua.
Giải:
Số học viên 3 lớp là: 38 + 42 + 45 = 125 (học viên)
1 học viên được mua số vở là: 625 : 125 = 5 (vở)
Lớp 4A được mua: 5 x 38 = 190 (vở)
Lớp 4B được mua: 5 x 42 = 210 (vở)
Lớp 4C được mua: 5 x 45 = 225 (vở)
Bài 2. Cô giáo chia 720 quyển vở cho 3 lớp. Biết 3 lần số vở của lớp 4A bằng hai lần số vở của lớp 4B, 5 lần số vở của lớp 4B bằng 3 lần số vở của lớp 4C. Tìm số vở của mỗi lớp.
Giải:
Theo đề bài ta có nếu biểu thị số vở 4B là 3 phần thì số vở của lớp 4A là 2 phần, số vở của lớp 4C là 5 phần. Ta có sơ đồ:
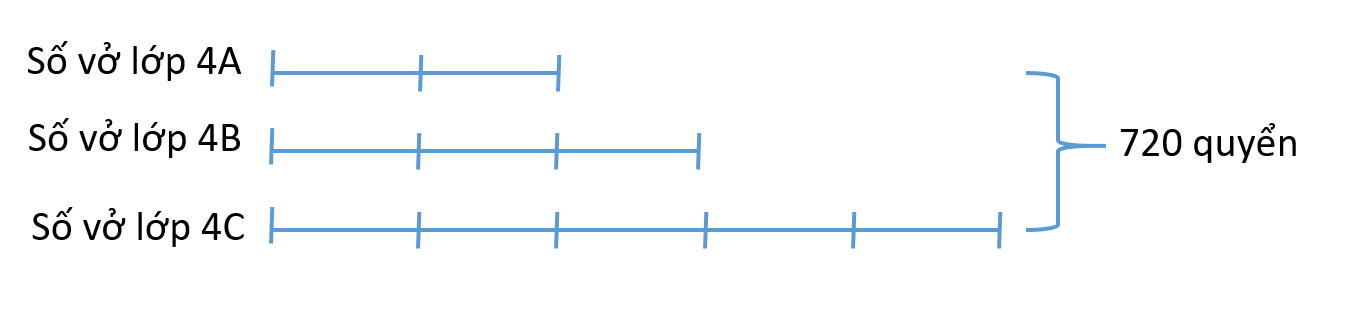
Tổng số phần bằng nhau là: 2 + 3 + 5 = 10 (phần)
Số vở 4A là: 720 : 10 x 2 = 144 (quyển)
Số vở 4B là: 144 : 2 x 3 = 216 (quyển)
Số vở 4C là: 216 : 3 x 5 = 360 (quyển)
Bài 3. Hai đội thiếu niên tiền phong, đội 1 có 4 phân đội, đội 2 có 5 phân đội. Đội 1 kém đội 2 là 12 bạn. Biết số đội viên mỗi phân đội bằng nhau, tính xem cả hai đội có bao nhiêu đội viên?
Phân tích: Vì đội 2 nhiều hơn nữa đội 1 là một trong phân đội, mà đội 2 nhiều hơn nữa đội 1 là 12 bạn nên số bạn 1 phân đội là 12 bạn. Từ đó ta tính được số đội viên mỗi đội.
Giải:
Số phân đội của đội 2 hơn đội 1 là:
5 – 4 = 1 (phân đội)
Đội 1 kém đội 2 là 12 bạn, vậy 1 phân đội có 12 bạn.
Số đội viên đội 1 là: 12 x 4 = 48 (bạn)
Số đội viên đội 2 là: 12 x 5 = 60 (bạn)
Số đội viên của tất cả hai đội là: 48 + 60 = 108 (bạn)
Bai 4. Một shop bán xà phòng, buổi sáng bán được 5 thùng, buổi chiều bán được 5 hộp. Biết buổi sáng bán nhiều hơn nữa buổi chiều 100 gói và số gói ở mỗi thùng buổi sáng nhiều gấp hai số gói ở mỗi hộp buổi chiều. Hỏi buổi sáng, buổi chiều bán được bao nhiêu gói xà phòng?
Giải:
Buổi sáng bán nhiều hơn nữa buổi chiều: 5 x 2 – 5 = 5 (hộp buổi chiều)
1 hộp buổi chiều có số gói là: 100 : 5 = 20 (gói)
Số gói bán buổi sáng là: 20 x 5 x 2 = 200 (gói)
Số gói bán buổi chiều là: 20 x 5 = 100 (gói)
Bài 5. Có 4 đoàn xe, đoàn 1 gồm những xe, mỗi xe chở được 15 tạ, đoàn 2 gồm những xe, mỗi xe chở được 2 tấn, đoàn 3 gồm những xe, mỗi xe chở được 25 tạ và đoàn 4 gồm những xe, mỗi xe chở được 3 tấn. Cả bốn đoàn chở được 450 tạ gạo. Tính xem mỗi đoàn chở bao nhiêu tạ gạo, biết số xe của 4 đoàn bằng nhau.
Giải:
2 tấn = 20 tạ
3 tấn = 30 tạ.
Vì số xe của 4 đoàn bằng nhau nên ta giả sử mỗi đoàn đều có một xe thì số tạ gạo chở được là:
15 + 20 + 25 + 30 = 90 (tạ)
Số xe mỗi đoàn là: 450 : 90 = 5 (xe)
Đoàn 1 chở được: 15 x 5 = 75 (tạ)
Đoàn 2 chở được: 20 x 5 = 100 (tạ)
Đoàn 3 chở được: 25 x 5 = 125 (tạ)
Đoàn 4 chở được: 30 x 5 = 150 (tạ)
Bài 6. Trong một đợt kiểm tra, ba lớp 4A, 4B, 4C được tất cả 130 điểm 10. Biết số điểm 10 của lớp 4B gấp hai số điểm 10 của lớp 4A và gấp rưỡi số điểm 10 của lớp 4C. Tính xem mỗi lớp có bao nhiêu điểm 10.
Giải:
Vì số điểm 10 của lớp 4B gấp hai số điểm 10 của lớp 4A và gấp rưỡi số điểm 10 của lớp 4C và tổng số điểm 10 là 130 nên ta có sơ đồ : ( biểu thị số điểm 10 của lớp 4B là 6 phần bằng nhau), thì số điểm 10 của lớp 4A là 3 phần và số điểm 10 của lớp 4C là 4 phần như vậy.

Số điểm 10 lớp 4A là:
130 : (6 + 4 + 3) x 3 = 30 (điểm)
Số điểm 10 lớp 4B là: 30 x 2 = 60 (điểm)
Số điểm 10 lớp 4C là: 130 – 60 – 30 = 40 (điểm)
Bài 7. Cô giáo mua vở cho học viên 66 000 đồng, gồm ba loại 200 đồng, 400 đồng và 500 đồng một quyển. Số tiền mua vở mỗi loại đều bằng nhau. Hỏi mỗi loại có bao nhiêu quyển vở?
Giải:
Vì số tiền mua mỗi loại vở đều bằng nhau nên:
Số tiền mua mỗi loại vở là: 66 000 : 3 = 22 000 (đồng)
Số vở loại 200 đồng là: 22 000 : 200 = 110 (quyển)
Số vở loại 400 đồng là: 22 000 : 400 = 55 (quyển)
Số vở loại 500 đồng là: 22 000 : 500 = 44 (quyển)
Bài 8. Hai công nhân được thưởng 96 000 đồng. Biết 1/3 tiền thưởng của người thứ nhất bằng 1/5 tiền thưởng của người thứ hai. Hỏi từng người được thưởng bao nhiêu?
Giải:
Vì 1/3 số tiền thưởng của người thứ nhất bằng 1/5 số tiền thưởng của người thứ hai và tổng số tiền thưởng của 2 người là 96 000 đồng nên ta có sơ đồ:

Số tiền thưởng của người thứ nhất là: 96000 : (3 + 5 ) x 3 = 36 000 (đồng)
Số tiền thưởng của người thứ hai là: 96000 – 36000 = 60000 (đồng)
Bài 9. Cho 3 số có tổng bằng 550. Biết số thứ nhất bằng 1/2 số thứ ba, số thứ ba gấp 3 lần số thứ hai. Tìm ba số đó.
Giải:
Vì số thứ nhất bằng 1/2 số thứ 3, số thứ ba gấp 3 lần số thứ 2 nên biểu thị số thứ ba là 6 phần bằng nhau thì số thứ nhất sẽ là 3 phần như vậy, số thứ hai sẽ là 2 phần như vậy.
Tổng của chúng bằng 550 nên ta có sơ đồ:

Tổng số phần bằng nhau: 3 + 2 + 6 = 11 (phần)
Số thứ 1 là: 550 : 11 x 3 = 150
Số thứ 3 là: 150 x 2 = 300
Số thứ 2 là: 300 : 3 = 100
Bài 10. Hai nhà máy sản xuất A và B có 2550 công nhân. Nếu thêm vào nhà máy sản xuất B 200 người và giảm sút ở nhà máy sản xuất A 200 người thì khi đó số công nhân ở nhà máy sản xuất A sẽ bằng 1/2 số công nhân của nhà máy sản xuất B. Tìm xem lúc đầu mỗi nhà máy sản xuất có bao nhiêu công nhân.
Giải:
Thêm vào nhà máy sản xuất B 200 người, giảm nhà máy sản xuất A 200 người thì tổng số công nhân hai nhà máy sản xuất vẫn là 2550 người. Số công nhân ở mỗi nhà máy sản xuất sau khi đã thay đổi biểu thị theo sơ đồ sau:
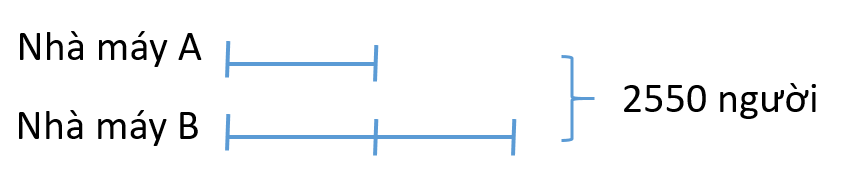
Số công nhân ở nhà máy sản xuất A sau khi giảm 200 người là:
2550 : ( 1 + 2 ) = 850 (người)
Số công nhân lúc đầu ở nhà máy sản xuất A là:
2550 – 1050 = 1500 (người)
Bài tập tự luyện.
Bài 1. An đi từ nhà tới trường mất 20 phút, từ trường đến câu lạc bộ thiếu niên mất 25 phút, quãng đường từ trường đến câu lạc bộ dài hơn thế nữa quãng đường từ nhà đến trường là 325m. Hỏi từ nhà đến trường dài bao nhiêu mét? Từ trường đến câu lạc bộ dài bao nhiêu mét?
Bài 2. Tìm hai số có tổng là 1991 và thương của chúng là 1990.
Bài 3. Mẹ có 10 200 đồng gồm 3 loại tiền : loại 200 đồng, loại 500 đồng và 1000 đồng. Biết số tờ mỗi loại bằng nhau, tính xem mỗi loại có bao nhiêu đồng.
Bài 4. Một shop bán được 150 000 đồng tiền hàng, trong đó 1/3 tiền bán hàng may mặc bằng ½ tiền bán đồ nhôm và bằng 1/5 tiền bán đồ điện. Hỏi shop đó đã bán được bao nhiêu tiền hàng mỗi loại?
Bài 5. Có hai thùng kẹo. Nếu thêm 200 gói vào thùng thứ nhất thì số gói kẹo ở hai thùng bằng nhau, nếu thêm 300 gói vào thùng thứ hai thì số gói kẹo ở thùng thứ hai sẽ gấp hai số kẹo ở thùng thứ nhất. Tìm số gói kẹo ở mỗi thùng.
Bài 6. Hai kho thóc, kho A có 3200 tấn, kho B có 5600 tấn. Nếu chuyển đi ở mỗi kho cùng một số trong những thóc nào đó thì số thóc còn sót lại của kho B gấp hai số thóc ở kho A. Tìm số thóc đã chuyển đi ở mỗi kho.
Bài 7. Lớp 4A và 4B sẵn sàng sẵn sàng 96 000 đồng để mua phần thưởng thời điểm ở thời điểm cuối năm. Lớp 4A đã mua hết 10 000 đồng, lớp 4B mua hết 26 000 đồng khi đó số tiền còn sót lại của lớp 4A gấp hai số tiền còn sót lại của lớp 4B. Hỏi lúc đầu mỗi lớp sẵn sàng sẵn sàng bao nhiêu tiền mua phần thưởng?
Bài 8. Tổ An và Bình mua một số trong những vở. Biết số vở của tổ An ít hơn số vở của tổ Bình là 30 quyển và 1/3 số vở tổ Bình bằng ½ số vở tổ An. Tìm số vở tổ An, tổ Bình đã mua.
Bài 9. An và Bình có một số trong những tiền. Biết số tiền của Bình bằng ½ số tiền của An và Bình nếu thêm 200 đồng, An có thêm 1600 đồng thì lúc đó số tiền của An sẽ gấp 3 lần số tiền của Bình. Tìm số tiền lúc đầu của từng người.
Bài 10. Trong một trường ngoại ngữ học buổi tối số người học tiếng Đức bằng ½ số người học tiếng Pháp, số người học tiếng Pháp bằng 1/3 số người học tiếng Anh. Hỏi mỗi ngoại ngữ có bao nhiêu người học, biết số người học tiếng Anh nhiều hơn nữa số người học tiếng Đức là 100 người?
Bài 11. Ba người đi bằng ba loại xe rất khác nhau từ A đến B. Thời gian người thứ nhất đi bằng 1/3 thời gian người thứ ba đi và bằng 1/2 thời gian người thứ hai đi. Biết 1 giờ người thứ hai đi được 24km và thời gian người thứ ba đi là 135 phút, tính quãng đường AB.
Toán học là một môn học chiếm thời gian đáng kể trong kế hoạch đào tạo của nhà trường Tiểu học. Không ai hoàn toàn có thể phủ nhận kĩ năng ứng dụng rộng rãi những kiến thức và kỹ năng Toán học vào môi trường tự nhiên thiên nhiên sống đời thường, vì thế việc dạy và học toán ra làm sao đã thu hút mọi sự quan tâm của giáo viên, học viên và toàn xã hội. Vì vậy mà Toán học đã thu hút được nhiều nhà khoa học, nhà sư phạm nghiên cứu và phân tích cách dạy và học những mạch kiến thức và kỹ năng Toán học cho hiệu suất cao nhất để vừa đảm bảo được tính phổ thông vừa đảm bảo tính khoa học.
Nhưng Toán học cũng đòi hỏi ở mỗi học viên sự lôi kéo tất cả vốn kiến thức và kỹ năng Toán học vào hoạt động và sinh hoạt giải trí giải toán và để hình thành những kĩ năng giải toán. Đòi hỏi học viên phải có lối tư duy khoa học và có vốn kiến thức và kỹ năng tổng hợp: Tiếng Việt, Tự nhiên- Xã hội. Mỗi bài toán được thể hiện qua những thuật toán và ẩn dưới những dạng toán, mang tính chất chất khối mạng lưới hệ thống có quan hệ mật thiết với nhau.
Để góp thêm phần nâng cao hiệu suất cao dạy học toán ở tiểu học và khắc phục những lỗi sai của học viên tôi đã đầu tư thời gian nghiên cứu và phân tích và mạnh dạn đưa ra vấn đề "Vận dụng phương pháp chia tỉ lệ vào dạy học giải toán".
Bạn đang xem 20 trang mẫu của tài liệu "Sáng kiến kinh nghiệm tay nghề Vận dụng phương pháp chia tỉ lệ vào dạy học giải toán Tiểu học", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ữ số thì được một số trong những mới tăng lên 220 đơn vị và gấp 12 lần số ban đầu. Tìm số tự nhiên đó. Lời giải Gọi số cần tìm là . Khi viết thêm chữ số 4 vào giữa ta được Theo bài ra ta có sơ đồ sau: : 220 : Số tự nhiên cần tìm là: (220 : 11) x 1 = 20 Đáp số: Số tự nhiên đó là 20 IV. Cấu tạo phân số 1. Kiến thức cơ bản. - Khi thêm vào đó cả tử và mẫu của một phân số với cùng một số trong những tự nhiên thì hiệu giữa tử và mẫu của phân số đó không thay đổi. - Khi bớt đi ở cả tử và mẫu của một phân số với cùng một số trong những tự nhiên thì hiệu giữa tử và mẫu của phân số đó không thay đổi. - Nếu ta thêm vào đó vào tử số đồng thời bớt đi ở mẫu số của phân số với cùng một số trong những tự nhiên thì tổng của tử và mẫu của phân số đó không thay đổi. - Nếu ta bớt đi ở tử và thêm vào ở mẫu của phân số với cùng một số trong những tự nhiên thì tổng của tử và mẫu của phân số đó không thay đổi. 2. Bài toán phát triển. Ví dụ 1: Khi thêm vào đó vào cả tử và mẫu của phân số với cùng một số trong những tự nhiên ta được một phân số mới bằng . Tìm số tự nhiên đó. Lời giải Hiệu của mẫu và tử số của phân số đã cho là: 29 - 11 = 18 (đơn vị) Phân số mới nhận được bằng nghĩa là nếu ta chia mẫu số thành 2002 phần bằng nhau thì tử số của nó chiếm 1999 phần như vậy. Mặt khác, khi thêm vào đó vào cả tử và mẫu của phân số với cùng một số trong những tự nhiên thì hiệu giữa tử và mẫu của phân số đó không thay đổi: 18 đơn vị 1999 phần 2002 phần Tử số của phân số mới: Mẫu số của phân số mới: Tử số của phân số mới là: 18 : (2002 - 1999) 1999 = 11994 (đơn vị) Số tự nhiên cần tìm là: 11994 - 11 = 11983. Ví dụ 2: Khi bớt đi ở cả tử và mẫu của phân số với cùng một số trong những tự nhiên ta nhận được một phân số bằng . Tìm số tự nhiên đó. Lời giải Hiệu giữa tử và mẫu của phân số đã cho là: 271 - 151 = 120 (đơn vị). ? 120 Ta có sơ đồ: Tử số mới: Mẫu số mới: Mẫu số của phân số mới là: 120 : (7 - 3) x 3 = 90 (đơn vị) Số tự nhiên cần tìm là: 151 - 90 = 61. Ví dụ 3: Tìm một phân số, biết rằng tổng của tử số và mẫu số của nó bằng 210 và sau khi rút gọn phân số đó bằng . Lời giải Khi rút gọn phân số mới ta được , nghĩa là nếu mẫu số của phân số đó được phân thành 9 phần bằng nhau thì tử số sẽ chiếm 5 phần như vậy. 210 đơn vị ? ? Ta có sơ đồ sau: Tử số: Mẫu số: Tử số của phân số cần tìm là: 210 : (5 + 9) x 5 = 75 (đơn vị) Mẫu số của phân số cần tìm là: 210 - 75 = 135 (đơn vị) Phân số cần tìm là:. Ví dụ 4: Khi thêm vào đó vào tử số và bớt đi ở mẫu số của phân số với cùng một số trong những tự nhiên, ta nhận được một phân số bằng . Tìm số tự nhiên đó. Lời giải Tổng số của tử và mẫu của phân số đã cho là: 43 + 67 = 110 (đơn vị) Phân số mới là . Nếu gọi tử số là 6 phần bằng nhau thì mẫu số sẽ là 5 phần như vậy. ? 110 đơn vị Ta có sơ đồ: Tử số mới: Mẫu số mới: Tử số của phân số mới là: 110 : (6 + 5) x 6 = 60 (đơn vị) Số tự nhiên cần tìm là: 60 - 43 = 17. Ví dụ 5: Khi bớt đi ở tử đồng thời thêm vào đó vào mẫu của phân số với cùng một số trong những tự nhiên ta được một phân số mới . Tìm số tự nhiên đó. Lời giải Tổng của tử số và mẫu số của phân số đã cho là: 151 + 49 = 200 (đơn vị). 13 phần 7 phần ? 200 đơn vị Ta có sơ đồ: Tử số mới: Mẫu số mới: Mẫu số của phân số mới là: 200 : (13 + 7) 7 = 70 (đơn vị). Số tự nhiên cần tìm là: 70 - 49 = 21. V. Cấu tạo số thập phân. 1. Kiến thức cơ bản - Khi dời dấu phẩy của một số trong những thập phân từ phải qua trái một, hai hoặc ba hàng thì số đó giảm sút 10, 100, hoặc 1000 lần. - Khi dời dấu phẩy của một số trong những thập phân từ trái qua phải một, hai hoặc ba hàng thì số đó tăng lên 10, 100 hoặc 1000 lần. 2. Bài toán cơ bản. Ví dụ 1: Khi dời dấu phẩy của một số trong những thập phân sang bên trái một hàng thì số đó giảm sút 319,14 đơn vị. Tìm số đó. Lời giải ? 319,14 Khi lùi dấu phẩy sang bên trái một hàng thì số đó giảm sút 10 lần. Ta có sơ đồ sau: Số cần tìm: Số mới: Số thập phân cần tìm là: 319,14 : (10 - 1) x 10 = 354,6. Vậy số cần tìm là: 354,6. Ví dụ 2: Tìm một số trong những thập phân có hai chữ số ở phần thập phân, biết rằng khi bỏ quên dấu phẩy của số đó thì nó tăng thêm 1221,66 đơn vị. Lời giải ? 100 phần 1221,66 đơn vị Vì số thập phân cần tìm có hai chữ số ở phần thập phân nên khi bỏ quên dấu phẩy thì số đó tăng gấp 100 lần. Ta có sơ đồ biểu thị quan hệ giữa số thập phân cần tìm và số mới nhận được khi bỏ quên dấu phẩy: Số cần tìm: Số mới: Số thập phân cần tìm là: 1221,66 : (100 - 1) = 12,34. Vậy số cần tìm là: 12,34. 3. Bài toán tích hợp. Ví dụ 1: Khi cộng một số trong những tự nhiên với một số trong những thập phân có một chữ số ở phần thập phân, do sơ suất, một học viên đã bỏ quên dấu phẩy của số thập phân và đặt phép cộng như cộng hai số tự nhiên nên kết quả đã tăng thêm 110,7 đơn vị. Tìm số thập phân đó. Lời giải Khi bỏ quên dấu phẩy của số thập phân có một chữ số ở phần thập phân thì số đó tăng gấp 10 lần. Ta có sơ đồ sau: TN TP TN 110,7 Phép tính đúng: Phép tính chép nhầm: Số thập phân cần tìm là: 110,7 : (10 - 1)= 12,3. Vậy số cần tìm là: 12,3. Ví dụ 2: Khi trừ một số trong những tự nhiên cho một số trong những thập phân, do sơ suất, một học viên đã chép nhầm dấu phẩy của số thập phân lùi sang bên trái một hàng nên kết quả đã tăng thêm 48,87 đơn vị. Tìm số thập phân đó. Lời giải Khi dời dấu phẩy của số thập phân qua bên trái một hàng thì số đó giảm sút 10 lần. Ta có sơ đồ: Số TP cần tìm TN 48,87 TP mới Phép tính đúng: Phép tính chép nhầm: Số thập phân cần tìm là: 48,87 : (10 - 1) = 5,43. Vậy số cần tìm là: 5,43. VI. Các bài toán có văn điển hình trên tập phân số. Ví dụ 1: Hai bà đi chợ bán ổi. Sau khi nhẩm tính, một bà bảo: " số ổi của tôi gấp 1,5 lần số ổi của bà và số ổi của tôi nhiều hơn nữa số ổi của bà là 20 quả". Hỏi mỗi bà đã mang bao nhiêu ổi ra chợ bán? Lời giải ? quả 20 quả ? quả Ta có sơ đồ sau: số ổi của bà thứ nhất: số ổi của bà thứ hai: Ba phần năm số ổi của bà thứ nhất là: 20 : (3 - 2) x 3 = 60 (q.ả) Năm phần tám số ổi của bà thứ hai là: 60 - 20 = 40 (quả). Số ổi của bà thứ nhất là: 60 : 3 x 5 = 100 (quả). Số ổi của bà thứ hai là: 40 : 5 x 8 = 64 (quả). Đáp số: Bà thứ nhất có 100 quả ổi Bà thứ hai có 64 quả ổi. Ví dụ 2: Một shop rau quả có hai rổ đựng cam và chanh. Sau khi bán được số cam và số chanh thì người bán hàng thấy còn sót lại 160 quả hai loại, trong đó số cam bằng số chanh. Hỏi lúc đầu shop có bao nhiêu quả mỗi loại? Lời giải Cách 1: Phân số chỉ số cam còn sót lại là: 1 - = . Phân số chỉ số chanh còn sót lại là: 1 - = . ? quả ? quả 160 quả Ta có sơ đồ sau: số cam: số chanh: Ba phần bảy số cam của shop là: 160 : (3 + 5) x 3 = 60 (quả). Bốn phần chín số chanh của shop là: 160 - 60 = 100 (quả). Số cam lúc đầu là: 60 : 3 x 7 = 140 (quả). Sô chanh lúc đầu của shop là: 100 : 4 x 9 = 225 (quả). Đáp số: 140 quả cam 225 quả chanh. Cách 2: ? quả ? quả 160 quả Ta có sơ đồ: Số cam còn sót lại: Số chanh còn sót lại: Số cam còn sót lại là: 180 : (3 + 5) x 3 = 60 (quả). Số chanh còn sót lại là: 160 - 60 = 100 (quả). Tiếp theo ta có sơ đồ: Bán Bán Còn 60 quả Còn 100 quả Số cam lúc đầu: Số chanh lúc đầu: Số cam lúc đầu là: 60 : 3 x 7 = 140 (quả). Số chanh lúc đầu là: 100 : 4 x 9 = 225 (quả). Đáp số: 140 quả cam. 225 quả chanh. VII. Toán có nội dung hình học. 1. Bài toán cơ bản. Một hình chữ nhật có nửa chu vi là 50 mét, trong đó chiều dài gấp 4 lần chiều rộng. Tìm chiều dài và chiều rộng của hình chữ nhật đó. Lời giải ? m ? m 50 m Ta có sơ đồ: Chiều dài: Chiều rộng: Chiều rộng của hình chữ nhật là : 50 : (4 + 1) = 10 (m) Chiều dài của hình chữ nhật là : 10 4 = 40 (m) Đáp số: Chiều rộng: 10m. Chiều dài: 40m. 2. Bài toán phát triển. Ví dụ 1: Một thửa ruộng hình chữ nhật có chu vi 120 mét, trong đó chiều rộng bằng chiều dài. Tìm diện tích s quy hoạnh của thửa ruộng đó. Lời giải Nửa chu vi của thửa ruộng đó là: 120 : 2 = 60 (m) 60 mét ? m ? m Ta có sơ đồ sau: Chiều rộng : Chiều dài : Chiều rộng của thửa ruộng là : 60 : (5 + 7) 5 = 25 (m). Chiều dài của thửa ruộng là : 60 - 25 = 35 (m). Diện tích thửa ruộng là : 25 35 = 875 (mét vuông). Đáp số : 875 mét vuông. Ví dụ 2: Người ta mở rộng một chiếc ao hình vuông vắn về bốn phía như trên hình vẽ. Sau khi mở rộng, diện tích s quy hoạnh ao tăng thêm 300 mét vuông và như vậy diện tích s quy hoạnh ao mới gấp 4 lần diện tích s quy hoạnh ao cũ. Hỏi người ta cần dùng bao nhiêu chiếc cọc để rào đủ xung quanh cái ao mới ? Biết rằng cọc nọ cách cọc kia là một trong mét. 300 mét vuông Lời giải Ta có sơ đồ sau : ? 300 mét vuông Diện tích ao cũ : Diện tích ao cũ : Diện tích ao mới là : 300 : (4 - 1) x 4 = 400 (mét vuông). Suy ra cạnh của ao mới là 20m, vì 20 x 20 = 400. Chu vi của ao mới là : 20 x 4 = 80 (m). Số cọc cần để rào xung quanh ao mới là : 80 : 1 = 80 (chiếc). Đáp số : 80 chiếc cọc. Ví dụ 3 : Hình lớn Hình nhỏ Có hai mảnh bìa hình vuông vắn mà cạnh của mảnh lớn gấp hai cạnh của mảnh nhỏ. Người ta cắt hai mảnh bìa đó thành những mảnh nhỏ rồi ghép lại được một hình vuông vắn có diện tích s quy hoạnh bằng 20 cm2. Tìm cạnh của mỗi mảnh bìa đó. Lời giải Nhìn vào hình vẽ ta thấy diện tích s quy hoạnh của hình vuông vắn lớn gấp 4 lần diện tích s quy hoạnh hình vuông vắn nhỏ. Ta có sơ đồ : ? cm2 ? cm2 20 cm2 Diện tích hình nhỏ : Diện tích hình lớn : Diện tích hình vuông vắn nhỏ là : 20 : (1 + 4) = 4 (cm2). Suy ra cạnh hình vuông vắn nhỏ bằng 2cm, vì 2 x 2 = 4. Diện tích hình vuông vắn là : 20 - 4 = 16 (cm2). Suy ra cạnh hình vuông vắn lớn bằng 4cm, vì 4 x 4 = 16. Đáp số : 2cm và 4cm. VIII. Các bài toán về hoạt động và sinh hoạt giải trí đều 1. Kiến thức cơ bản. - Trên cùng một quãng đường, vận tốc và thời gian là hai đại lượng tỷ lệ nghịch. - Trong cùng thuở nào gian, quãng đường và vận tốc là hai đại lượng tỷ lệ thuận. - Với cùng một vận tốc, quãng đường và thời gian là hai đại lượng tỷ lệ thuận. 2. Các bài toán phát triển. Ví dụ 1 : Một người dự kiến đi xe đạp từ nhà với tốc độ 14km/ giờ để đến huyện lúc 10 giờ. Do trở gió nên xe mỗi giờ chỉ đi được 10km và đến huyện lúc 10 giờ 36 phút. Tính quãng đường từ nhà lên huyện. Lời giải Thời gian người ấy đi lâu hơn so với dự kiến là : 10 giờ 36 phút - 10 giờ = 36 phút. Tỉ số giữa hai vận tốc là : . Trên cùng quãng đường từ nhà lên huyện thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau. Vì vậy nếu ta màn biểu diễn thời gian đi thực là 7 phần bằng nhau thì thời gian dự tính đi sẽ là 5 phần như vậy. ? phút 36 phút Ta có sơ đồ sau : Thời gian thực đi : Thời gian dự kiến đi : Thời gian xe thực đi là: 36 : (7 - 5) 7 = 126 (phút). 126 phút = giờ. Quãng đường từ nhà lên huyện là: 10 = 21 (km). Đáp số: 21km. Ví dụ 2: Lúc 7 giờ sáng, một ô tô xuất phát từ A với vận tốc 45 km/giờ đi về phía tỉnh B. Cùng lúc đó một người đi xe máy xuất phát từ B với vận tốc 35 km/giờ đi về phía tỉnh A. Hỏi lúc mấy giờ thì hai xe gặp nhau và chỗ gặp nhau cách A bao xa? Biết rằng quãng đường từ A đến B dài 160km. Lời giải Cách 1: Tỉ lệ vận tốc của ô tô và xe máy là: Vì trong cùng khoảng chừng thời gian thì quãng đường và vận tốc là hai đại lượng tỉ lệ thuận nên nếu ta chia quãng đường từ A đến địa điểm gặp nhau thành 9 phần bằng nhau thì quãng đường từ B đến địa điểm gặp nhau sẽ chiếm 7 phần. Vậy ta có sơ đồ: ? km 160km Quãng đường từ A đến chỗ gặp nhau : Quãng đường từ B đến chỗ gặp nhau : Quãng đường từ A đến chỗ gặp nhau là : 160 : (9 + 7) x 9 = 90 (km). Thời gian đi từ A đến chỗ gặp nhau là: 7 + 2 = 9 (giờ). Đáp số: 9 giờ, 90 km. Cách 2: Thời gian để hai xe đến chỗ gặp nhau là: 160 : (45 + 35) = 2 (giờ). Thời điểm để hai xe gặp nhau là: 7 + 2 = 9 (giờ). Quãng đường từ A đến chỗ gặp nhau là: 45 x 2 = 90 (km). Ví dụ 3: Lúc 8 giờ sáng một xe khách khởi hành từ Tp Hà Nội Thủ Đô đi về đến Tỉnh Nam Định nghỉ lại 3 giờ để trả và đón khách, sau đó lại về đến Tp Hà Nội Thủ Đô lúc 3 giờ 30 phút chiều cùng trong ngày. Lúc trở về do đường ngược gió nên mỗi giờ đi chậm hơn lúc đi 9 km. Tính quãng đường từ Tp Hà Nội Thủ Đô đến Tỉnh Nam Định, biết rằng thời gian đi nhanh hơn thời gian lúc về 30 phút. Lời giải 3 giờ 30 phút chiều = 15 giờ 30 phút. Thời gian để ô tô đi và về là: 15 giờ 30 phút - 8 giờ - 3 giờ = 4 giờ 30 phút. Thời gian xe đi từ Tp Hà Nội Thủ Đô đến Tỉnh Nam Định là: (4 giờ 30 phút - 30 phút) : 2 = 2 giờ. Thời gian xe đi từ Tỉnh Nam Định về Tp Hà Nội Thủ Đô là: 4 giờ 30 phút - 2 giờ = 2 giờ 30 phút. Tỉ số thời gian lúc đi và lúc về là: 2 giờ : 2 giờ 30 phút = . Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch, suy ra tỉ số giữa vận tốc đi và vận tốc về là . 9 km/giờ ? Ta có sơ đồ sau: Vận tốc đi: Vận tốc về: Vận tốc của ô tô lúc đi là: 9: (5 - 4) x 5 = 45 (km/giờ). Quãng đường dài là: 45 x 2 = 90 (km). Đáp số: 90 km. IX. Tìm ba số lúc biết tổng và tỉ số của chúng. 1. Bài toán cơ bản. Tổng của ba số tự nhiên là 54. Trong số đó số thứ hai gấp 2 lần số thứ nhất, số thứ ba gấp ba lần số thứ 3. Tìm ba số đó. Lời giải Nêu biểu thị số thứ nhất là một phần thì số thứ là 2 phần như vậy. Vì số thứ ba gấp 3 lần số thứ 2 nên nếu số thứ hai được biểu thị bởi 2 đoạn thẳng bằng nhau thì số thứ ba được biểu thị bởi: 2 3 = 6 (phần). Ta có sơ đồ sau: 54 ? ? ? Số thứ nhất: Số thứ hai: Số thứ ba: Số thứ nhất là: 54 : (1 + 2 + 6) = 6. Số thứ hai là: 6 2 = 12. Số thứ ba là: 12 3 = 36. Đáp số: 6, 12, 36. 2. Bài toán phát triển. Ví dụ 1: Tổng của ba số tự nhiên bằng 189. Tỉ số của số thứ nhất so với số thứ hai bằng , tỉ số của số thứ hai so với số thứ ba bằng . Tìm ba số đó. Lời giải Tỉ số của số thứ hai so với số thứ ba bằng . Vì vậy nếu ta chia số thứ ba thành bốn phần bằng nhau thì số thứ hai sẽ chiếm ba phần như vậy. Tỉ số của số thứ nhất với số thứ hai bằng . Vì vậy nếu ta chia số thứ hai thành ba phần bằng nhau thì số thứ nhất sẽ chiếm hai phần như vậy. 189 ? ? ? Ta có sơ đồ sau: Số thứ nhất: Số thứ hai: Số thứ ba: Số thứ nhất là: 189 : (2 + 3 + 4) x 2 = 42. Số thứ hai là: 189 : (2 + 3+ 4) x 3 = 63. Số thứ ba là: 189 - (42 + 63) = 84. Trả lời: Ba số cần tìm là: 42, 63 và 84. Ví dụ 2: Ba xe vận tải được lôi kéo chở 480 tấn hàng cho một xí nghiệp chế biến thực phẩm. Số hàng xe thứ hai chở được bằng số hàng của xe thứ nhất và bằng số hàng của xe thứ ba. Hỏi mỗi xe đã chở được bao nhiêu tấn hàng? Lời giải Theo đề bài thì nếu chia số hàng của xe thứ hai thành 4 phần bằng nhau thì số hàng của xe thứ nhất sẽ chiếm 5 phần và số hàng của xe thứ ba sẽ chiếm 7 phần như vậy. Ta có sơ đồ sau: 480 tấn ? tấn ? tấn ? tấn Số hàng của xe thứ nhất: Số hàng của xe thứ hai: Số hàng của xe thứ ba: Số hàng xe thứ nhất chở được là: 480 : (5 + 4 + 7) 5 = 150 (tấn). Số hàng xe thứ hai chở được là: 480 : (5 + 4 + 7) 4 = 120 (tấn). Số hàng xe thứ ba chở được là: 480 - (150 + 120) = 210 (tấn). Đáp số: Xe thứ nhất chở được 150 tấn Xe thứ hai chở được 120 tấn. Xe thứ ba chở được 210 tấn. X. Tìm ba số lúc biết hiệu và tỉ số của chúng. 1. Bài toán cơ bản. Tìm ba số biết số thứ hai gấp 3 lần số thứ nhất, số thứ ba gấp 4 lần số thứ nhất và hơn số thứ nhất 12 đơn vị. Lời giải 12 ? ? Ta có sơ đồ sau: Số thứ nhất: Số thứ ba: Số thứ nhất là: 12 : (4 - 1)= 4. Số thứ ba là: 4 4 = 16. Số thứ hai là: 4 3 = 12. Đáp số: 4; 12; 16. 2. Bài toán phát triển. Ví dụ 1: Tìm ba số, biết rằng số thứ nhất bằng số thứ ba, bằng số thứ hai và kém số thứ hai 4 đơn vị. Lời giải ? ? 4 đơn vị Ta có sơ đồ sau: Số thứ nhất: Số thứ hai: Số thứ nhất là: 4 : (5 - 3) 3 = 6. Số thứ hai là: 6 + 4 = 10. Số thứ ba là: 6 : 3 4 = 8. Trả lời: Ba số cần tìm là 6, 10 và 8. Ví dụ 2: Tìm ba số, biết rằng số thứ nhất bằng số thứ hai, bằng số thứ ba và kém số thứ ba 21 đơn vị. Lời giải ? ? 21 đơn vị Ta có sơ đồ: Số thứ nhất: Số thứ ba: Số thứ nhất là: 21 : (7 - 4) 4 = 28. Số thứ ba là: 21 + 28 = 49. Số thứ hai là: 28 : 7 9 = 36. Trả lời: Ba số cần tìm là 28, 36 và 49. Ví dụ 3: Trong phong trào thi đua lập thành tích chào mừng ngày sinh nhật Bác Hồ ở một trường tiểu học, số điểm 10 của khối Năm đạt được gấp 3 lần số điểm 10 của khối Bốn. Số điểm 10 của khối Bốn bằng số điểm 10 của khối Ba và kém khối Ba 130 điểm 10. Hỏi mỗi khối đã đạt được bao nhiêu điẻm 10? Lời giải ? điểm ? điểm 140 điểm Ta có sơ đồ sau: Khối Ba: Khối Bốn: Số điểm 10 của khối Ba đạt được là: 140 : (5 - 3) x 5 = 325 (điểm). Số điểm 10 của khối Bốn đạt được là: 325 - 130 = 195 (điểm). Số điểm 10 của khối Năm đạt được là: 195 x 3 = 585 (điểm). Đáp số: Khối 3 đạt được 325 điểm 10. Khối 4 đạt được 195 điểm 10. Khối 5 đạt được 585 điểm 10. XI. Bài toán vui, toán cổ. Ví dụ 1: Một đàn trẻ đang chăn trâu trên cánh đồng. Một em trong bọn hô: "Lên ngựa, mỗi vị một con!". Thế là một em không còn trâu cưỡi. Phi được một đoạn, một em khác trong bọn lại hô: "Sang ngựa, hai vị một con!". Thế là một trâu không còn người cưỡi. Hỏi có bao nhiêu trẻ? Bao nhiêu trâu? Lời giải Sau khi thực hiện lệnh của em thứ hai: "Sang ngựa, hai vị một con" thì số trâu có người cưỡi bằng một nửa tổng số trâu. Mặt khác theo đề bài thì thời điểm hiện nay có một con trâu không còn người cưỡi. Ta có sơ đồ: 1 con Tổng số trâu: Số trâu có người cưỡi: Tổng số trâu là: 1 x 2 = 2 (con). Sau khi thực hiện lệnh của em thứ nhất thì 1 em không còn trâu cưỡi. Vậy số trẻ hơn số trâu là một trong. Vậy số trẻ là: 2 + 1 = 3 (em). Đáp số: 3 trẻ; 2 trâu. Ví dụ 2: Một đàn cò bay đến đậu ở một vườn cây. Nếu mỗi cò đậu một cây thì 3 cò không còn cây đậu. Nếu mỗi cây 3 cò đậu thì 3 cây không còn cò đậu. Hỏi có tất cả bao nhiêu cây? Bao nhiêu cò? Lời giải Cách 1: Giả sử trong vườn có thêm 3 cây. Vậy số cây bằng số cò. Khi 3 cò đậu 1 cây thì số cây có cò đậu bằng tổng số cây. Trong trường hợp này ta hoàn toàn có thể màn biểu diễn bởi sơ đồ sau: 3 cây 3 cây Số cây không còn cò đậu Số cây có cò đậu Số cây thực có là: 3 3 - 3 = 6 (cây). Số cò là: 6 + 3 = 9 ( con). Cách 2: Giả sử có thêm 9 con cò (9 con này đậu vào 3 cây còn thừa thì mỗi cây có 3 cò đậu). Như vậy thời điểm hiện nay số cò gấp 3 lần số cây. Ta có sơ đồ: 3 con 9 con Số cây: Số cò: Số cò thực có là: (9 + 3) : 2 = 6 (con). Số cây là: 6 + 3 = 9 ( cây). Cách 3 : Giả sử bớt đi 3 cò. Như vậy số cò bằng số cây. Nếu 3 cò đậu 1 cây thì ta hoàn toàn có thể màn biểu diễn bởi sơ đồ sau: Cây không còn cò đậu Cây có cò đậu 1 cây 3 cây Số cây: Số cây là: (3 + 1) : 2 x 3 = 6 (cây). Số cò là: 6 + 3 = 9 (con). Đáp số: 6 cây; 9 cò. c/ phÇn kÕt luËn Thực tiễn xây dựng và phát triển sự nghiệp công nghiệp hoá, tân tiến hoá đất nước đang đòi hỏi những con người năng động, sáng tạo, tự lực, tự cường. Thế giới đã chuyển sang thời kì kinh tế tài chính tri thức, cho nên vì thế đầu tư vào chất xám sẽ là cách đầu tư hiệu suất cao nhất cho việc hưng thịnh của mỗi quốc gia. Cũng vì lí do này mà nhu yếu học tập của người dân ngày càng nhiều, trình độ dân trí ngày một tăng, quy mô xã hội học tập đang được hình thành và phát triển. Người dân ngày càng quan tâm tới việc học tập của con em của tớ mình. Chính vì vậy, là giáo viên, tất cả chúng ta phải không ngừng nghỉ nghiên cứu và phân tích, tìm tòi, phát hiện kiến thức và kỹ năng mới và kịp thời vận dụng những kiến thức và kỹ năng đó vào giảng dạy. Đặc biệt, đối với môn toán, giáo viên cần tìm ra phương pháp giải dễ hiểu nhất với học viên, phù phù phù hợp với tư duy trực quan của những em. Việc vận dụng phương pháp chia tỉ lệ vào giải toán đã góp một phần quan trọng vào việc phát triển tư duy cho học viên, từ những bài toán cơ bản đến những bài toán phát triển sẽ giúp học viên đi từ tư duy rõ ràng đến khái quát hoá, trừu tượng hoá. Phương pháp chia tỉ lệ giúp đơn giản hoá những dữ kiện trong bài, giúp học viên dễ hiểu, dễ nhớ, từ đó áp dụng giải nhiều bài toán phức tạp hơn ở lớp trên, bậc học trên. Đề tài này được hoàn thành xong dưới sự hướng dẫn, chỉ bảo của cô Vũ Thị Hoạch. §©y là lần đầu tiên tôi làm đề tài nghiên cứu và phân tích khoa học nên không tránh khỏi những thiếu sót, tôi rất mong nhận được những ý kiến đóng góp chân thành của những thầy cô và những bạn. H¶i D¬ng, ngµy 28 th¸ng 3 n¨m 2010 Sinh viªn thùc hiÖn: Ph¹m ThÞ BÝch TÀI LIỆU THAM KHẢO 1. Phương pháp dạy học giải toán ở tiểu học. Biên soạn: Vũ Quốc Chung (Chủ biên)- Đào Thái Lai- Đỗ Tiến Đạt- Trần Ngọc Lan- Nguyễn Hưng Quang- Lê Ngọc Sơn. 2. Thực hành giải toán tiểu học (Tập 1). Biên soạn: Trần Diên Hiển.
Tải thêm tài liệu liên quan đến nội dung bài viết Các bài toán về phương pháp chia tỉ lệ