Kinh Nghiệm Hướng dẫn Cho hình chóp S ABCD có đáy ABCD là hình thang AD là đáy lớn Chi Tiết
Bùi Xuân Trường đang tìm kiếm từ khóa Cho hình chóp S ABCD có đáy ABCD là hình thang AD là đáy lớn được Cập Nhật vào lúc : 2022-09-17 01:34:25 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.Nội dung chính
- Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD là đáy lớn). Gọi O, I lần lượt là giao điểm của AC và BD, của AB và CD. Giao tuyến của và là:
Bài tập trắc nghiệm 15 phút Bài toán về tìm giao tuyến hai mặt phẳng - Toán Học 11 - Đề số 2Video liên quan
Hay nhất
Xác định giao tuyến của (left(ABNright)) và (left(CDMright).)
Trong (left(ABCDright)), gọi (I=ABcap CD), trong (left(SACright),)
gọi (J=ANcap CM).
Ta có:(left{beginarrayl Iin ABsubset left(ABNright) \ Iin CDsubset left(CDMright) endarrayright. Rightarrow Iin left(ABNright)cap left(CDMright), , , left(1right).)
Mặt khác: (left{beginarrayl Jin ANsubset left(ABNright) \ Jin CMsubset left(CDMright) endarrayright. Rightarrow Jin left(ABNright)cap left(CDMright), , , left(2right).)
Từ (left(1right)) và (left(2right)) suy ra (left(ABNright)cap left(CDMright)=IJ. )
Tìm giao điểm của MN với (left(SBDright).)
Chọn (left(SACright)) chứa MN, trong (left(ABCDright)), gọi (O=ACcap BD).
Ta có: (Sin left(SACright)cap left(SBDright), , , left(3right).)
Mặt khác:( left{beginarrayl Oin ACsubset left(SACright) \ Oin BDsubset left(SBDright) endarrayright. Rightarrow Oin left(SACright)cap left(SBDright), , , left(4right))
Từ (left(3right)) và (left(4right))suy ra (left(SACright)cap left(SBDright)=SO.)
Trong (left(SACright)), gọi (H=MNcap SO.)
Ta có: (left{beginarrayl Hin MN \ Hin SOsubset left(SBDright) endarrayright. Rightarrow MNcap left(SBDright)=leftHright.)
Gọi P là một điểm thuộc cạnh AB.
Xác định thiết diện của hình chóp cắt bởi (left(MNPright). )
Trong (left(SACright)), gọi (K=MNcap AC).
Trong (left(ABCDright)), gọi (left{beginarrayl Q.=PKcap BC \ E=PKcap CD endarrayright. .)
Trong (left(SCDright)), gọi (F=ENcap SD).
Ta có: (left{beginarrayl left(MNPright)cap left(SABright)=MP \ left(MNPright)cap left(ABCDright)=PQ \ left(MNPright)cap left(SBCright)=QN \ left(MNPright)cap left(SCDright)=NF \ left(MNPright)cap left(SDAright)=FM endarrayright. .)
Vậy thiết diện của hình chóp cắt bởi (left(MNPright)) là ngũ giác MPQNF.
Cho hình chóp S.ABCD có đáy ABCD là hình thang,AD là đáy lớn và AD 2BC . Gọi M, N lần lượt là trung điểm của SB, SC, O AC BD .
a) Tìm giao tuyến của ABN và SCD.
b) Tìm giao điểm P của DN và SAB .
c) Gọi K AN DM . Chứng minh 3 điểm S, K, O thẳng hàng. Tính KS KO .
Các thắc mắc tương tự
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.
a) Chứng minh rằng OG // (SBC)
b) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB).
c) Giả sử điểm I nằm trong đoạn SC sao cho SC = 3SI/2. Chứng minh rằng SA // (BID).
Cho hình chóp S.ABCD có đáy là hình thang ( đáy lớn AD). Gọi O la giao điểm của AC và BD, I và J lần lượt là trung điểm của SB và SC.
a) Xác định giao điểm M của AI và (SCD).
b) Chứng minh IJ // (SAD).
c) Xác định thiết diện của hình chóp cắt bởi mp (P) qua I, song song với SD và AC.
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD là đáy lớn). Gọi O, I lần lượt là giao điểm của AC và BD, của AB và CD. Giao tuyến của và là:
A.
A.SI
B.
B.SO
C.
C.

D.
D.

Đáp án và lời giải
Đáp án:A
Lời giải:
 Đáp án A HD:Ta có:
Đáp án A HD:Ta có:  và
và  Vì
Vì  Từ (1) và (2)
Từ (1) và (2) 
Đáp án đúng là A
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 15 phút Bài toán về tìm giao tuyến hai mặt phẳng - Toán Học 11 - Đề số 2
Làm bài
Chia sẻ
Một số thắc mắc khác cùng bài thi.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CD. Giao tuyến của hai mp
 và
và  là đường thẳng song song với đường thẳng nào sau đây?
là đường thẳng song song với đường thẳng nào sau đây?
Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng
 và
và  là:
là:
Cho hình chóp S.ABCD với ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
 và
và  là:
là:
Cho hình chóp S.ABCD với ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
 và
và  là:
là:
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD là đáy lớn). Gọi O, I lần lượt là giao điểm của AC và BD, của AB và CD. Giao tuyến của
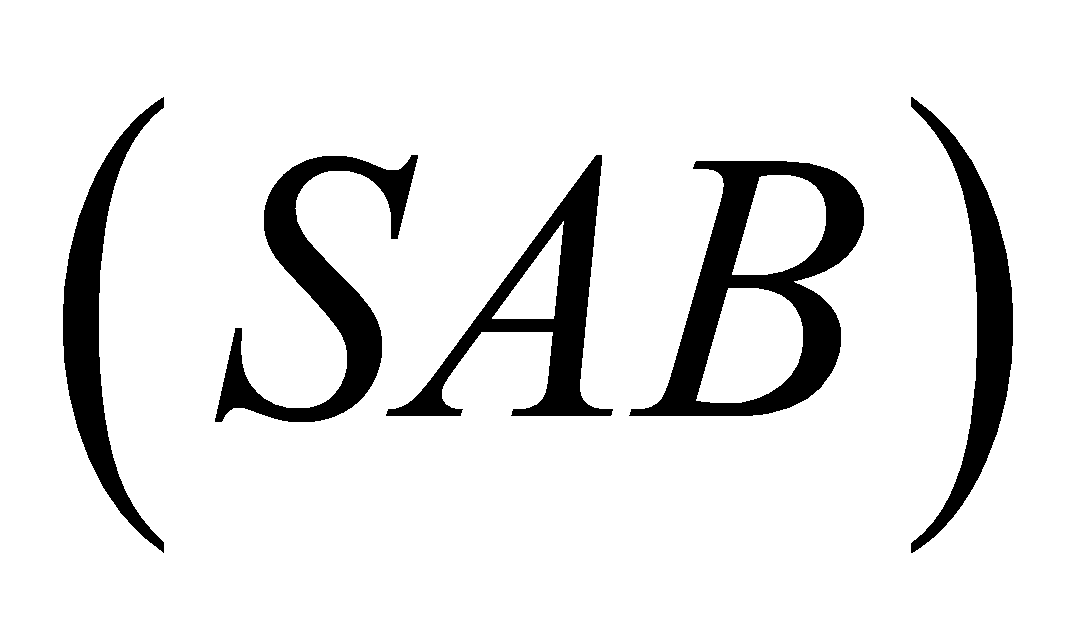 và
và 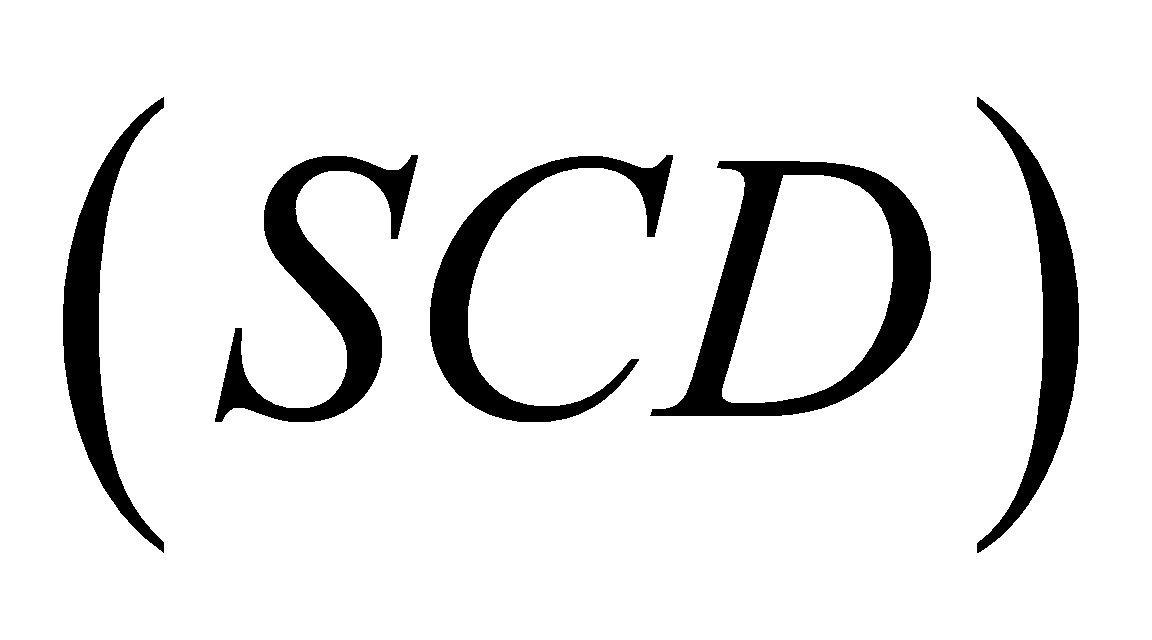 là:
là:
Cho bốnđiểm
 khôngđồngphẳng. Gọi
khôngđồngphẳng. Gọi lầnlượtlàtrungđiểmcủa
lầnlượtlàtrungđiểmcủa và
và Trênđoạn
Trênđoạn lấyđiểm
lấyđiểm saocho
saocho Giaođiểmcủađườngthẳng
Giaođiểmcủađườngthẳng vàmặtphẳng
vàmặtphẳng làgiaođiểmcủa
làgiaođiểmcủa
Cho đường thẳng d song song mặt phẳng
 và d nằm trong mặt phẳng
và d nằm trong mặt phẳng  . Gọi a là giao tuyến của
. Gọi a là giao tuyến của  và
và  . Khi đó:
. Khi đó:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông vắn tâm O. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
Cho hình chóp S.ABCD, I là giao điểm hai tuyến đường chéo của tứ giác ABCD. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CD. Giao tuyến của hai mp
 và
và  là đường thẳng song song với đường thẳng nào sau đây?
là đường thẳng song song với đường thẳng nào sau đây?
Một số thắc mắc khác hoàn toàn có thể bạn quan tâm.
She is terrified _______ snakes.
Điều kiện của tham số thực
 để phương trình
để phương trình  vô nghiệm là
vô nghiệm là
Tất cả những giá trị của tham số m để hàm số y=x4−2mx2+3 có ba cực trị là?
Cho m gam Mg vào dung dịch chứa 0,1mol AgNO3 và 0,25 mol Cu(NO3)2, sau thuở nào gian thu được 19,44 gam kết tủa và dung dịch X chứa 2 muối. Tách lấy kết tủa, thêm tiếp 8,4 gam bột sắt vào dung dịch X, sau khi những phản ứng hoàn toàn thu được 9,36 gam kết tủa. Giá trị của m là:
Cho tập
 có
có  phần tử. Tìm số tập con có
phần tử. Tìm số tập con có  phần tử của tập
phần tử của tập  .
.
_______, we’ll arrive before dark.
Someone had _______ left a window open.
Một tổ có
 học viên nam và
học viên nam và  học viên nữ. Hỏi có bao nhiêu cách chọn
học viên nữ. Hỏi có bao nhiêu cách chọn  học viên đi lao động, trong đó có
học viên đi lao động, trong đó có  học viên nam?
học viên nam?
She is capable ______ solving that problem.
Gọi
 là tập hợp những nghiệm thuộc khoảng chừng
là tập hợp những nghiệm thuộc khoảng chừng  của phương trình
của phương trình  . Tổng những phần tử của
. Tổng những phần tử của  là
là
