Kinh Nghiệm Hướng dẫn Cho tứ diện đều ABCD chứng tỏ AC vuông góc với BD Chi Tiết
Họ và tên đang tìm kiếm từ khóa Cho tứ diện đều ABCD chứng tỏ AC vuông góc với BD được Update vào lúc : 2022-09-11 10:50:10 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.Giới thiệu về cuốn sách này
Nội dung chính- Cho tứ diện (ABCD ) có (AB vuông góc CD ) và (AC vuông góc BD ). Gọi (H ) là hình chiếu vuông góc của (A ) lên (mp(BCD) ). Các xác định sau, xác định nào sai?CÂU HỎI HOT CÙNG CHỦ ĐỀVideo liên quanVideo liên quan
Giới thiệu về cuốn sách này
Cho tứ diện (ABCD ) có (AB vuông góc CD ) và (AC vuông góc BD ). Gọi (H ) là hình chiếu vuông góc của (A ) lên (mp(BCD) ). Các xác định sau, xác định nào sai?
Câu 8648 Vận dụng
Cho tứ diện (ABCD) có (AB bot CD) và (AC bot BD). Gọi (H) là hình chiếu vuông góc của (A) lên (mp(BCD)). Các xác định sau, xác định nào sai?
Đáp án đúng: d
Phương pháp giải
Phương pháp giải những bài toán đường thẳng vuông góc với mặt phẳng --- Xem rõ ràng
...
a. Cho tứ diện ABCD có AB ⊥ CD, AC ⊥ BD. Chứng minh rằng AD ⊥ BC. Vậy, những cạnh đối diện của tứ diện đó vuông góc với nhau. Tứ diện như vậy gọi là tứ diện trực tâm.. Câu 20 trang 103 SGK Hình học 11 Nâng cao – Bài 3: Đường thẳng vuông góc với mặt phẳng
a. Cho tứ diện ABCD có AB ⊥ CD, AC ⊥ BD. Chứng minh rằng AD ⊥ BC. Vậy, những cạnh đối diện của tứ diện đó vuông góc với nhau. Tứ diện như vậy gọi là tứ diện trực tâm.
b. Chứng minh những mệnh đề sau đây là tương đương :
i. ABCD là tứ diện trực tâm.
ii. Chân đường cao của tứ diện hạ từ một đỉnh trùng với trực tâm của mặt đối diện.
iii. (AB^2 + CD^2 = AC^2 + BD^2 = AD^2 + BC^2)
c. Chứng minh rằng bốn đường cao của tứ diện trực tâm đồng quy tại một điểm. Điểm đó gọi là trực tâm của tứ diện nói trên.
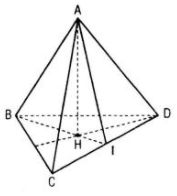
a. Kẻ AH ⊥ (BCD), H ϵ (BCD)
Ta có (left{ matrix CD bot AH cr CD bot AB cr right. Rightarrow CD bot left( ABH right))
Mà BH ⊂ (ABH) nên CD ⊥ BH (1)
Quảng cáoTương tự (left{ matrix BD bot AH cr BD bot AC cr right. Rightarrow BD bot left( ACH right) Rightarrow BD bot CH,left( 2 right))
Từ (1) và (2) suy ra H là trực tâm tam giác BCD.
Ta có: (left[AB2 cos60° + AB2 cos60° - AB2] = 0 Do đó MN 1 AB. Chứng minh tương tự ta có m/ / X / X / X / X / X / / ' X X 0 > X s^ X s' X s' X s' X y' X s' /N CD.MN = j[ÃD - ÃC].[ÃD + AC - ÃẼ Vậy MN 1 CD. BÀI TẬP LÀM THÊM Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm các cạnh AB, CD. Tính độ dài đoạn MN; Tính góc giữa các đường thẳng MN và BC, Chứng minh: MN 1 AB và MN 1 CD. -Hưártỹ iẫn Đặt BA = a, BC = c, BD = b => MN1CD. Cho hình lập phương ABCD.A'B'C'D'. Các điểm M, N lần lượt chia những đoạn thẳng AD' và DB theo cùng tỉ số k [k 0, 1]. Chứng minh rằng MN luôn luôn song song với mp[A'D'BC]; và chứng tỏ rằng nếu k = " thì: MN // A'C; c] MN 1 AD' và MN 1BD. D’ C’ A r B 'Hướng ỉẫn aj Đặt: AA' = a, AB = b, AD = C Theo giả thiết, ta có: MA = kMD' MA = k[MA + AD'] => ÃM = ~ÃẼT=-^-ía+c k-1 k-n —; AD-kAB c-kb 1-k 1-k Suy ra: MN = AN - AM = —77 c-kb + ka + kc AM = — 1-k 1-k k[a-b] + [k + l]c — BA' + ^^BC[l] -k 1-k v 7 1-k Đẳng thức [1] chứng tỏ MN, BA', BC đồng phẳng và do MN không thuộc mp[A'BCD'] nên MN // mp[A'BCD']. Khik = - ị thì [1] trở thành: MN = -^BA^ + ^BC = Ịã7C 2 3 3 3 Và do những đường thẳng MN và A'C cắt mp[ABCD] tại những điểm rất khác nhau nên chúng không trùng nhau. Vậy MN // A'C. Ta có: MN.AD' = “A'C.AD' =-j[b + c-a][c + a] =-^b^c+aj+^c -a ^ = 0 [Vì AB ± mp[ADD'A'] và ^a = c y Vậy MN 1 AD'.
Vẽ AH ⊥ [BCD] tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH
Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC
Vì AH ⊥ BC nên ta suy ra BC ⊥ AD
Cách khác: Trước hết ta hãy chứng tỏ hệ thức:
với bốn điểm A, B, C, D bất kì.
Thực vậy , ta có:
Do đó nếu AB ⊥ CD nghĩa là
Từ hệ thức [4] ta suy ra
do đó AD ⊥ BC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng [ABCD] và SA = a.
a] Chứng minh mặt phẳng [SAD] vuông góc với mặt phẳng [SDC], mặt phẳng [SAC] vuông góc với mặt phẳng [SCB].
b] Gọi φ là góc giữa hai mặt phẳng [SBC] và [ABCD], tính tanφ.
c] Gọi [α] là mặt phẳng chứa SD và vuông góc với mặt phẳng [SAC]. Hãy xác định [α] và xác định thiết diện của hình chóp S.ABCD với [α]
Xem đáp án » 04/05/2022 21,399
Hình hộp ABCD.A'B'C'D' có tất cả những cạnh đều bằng nhau. Chứng minh rằng AC ⊥ B'D', AB' ⊥ CD' và AD' ⊥ CB'. Khi mặt phẳng [AA'C'C] vuông góc với mặt phẳng [BB'D'D]?
Xem đáp án » 04/05/2022 3,640
Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh B và AC = 2a, có cạnh SA vuông góc với mặt phẳng [ABC] và SA = a
a] Chứng minh mặt phẳng [SAB] vuông góc với mặt phẳng [SBC].
b] Trong mặt phẳng [SAB] vẽ AH vuông góc với SB tại H, chứng tỏ AH ⊥ [SBC].
C] Tính độ dài đoạn AH.
d] Từ trung điểm O của đoạn AC vẽ OK vuông góc với [SBC] cắt [SBC] tại K. Tính độ dài đoạn OK.
Xem đáp án » 04/05/2022 3,271
Hình chóp S.ABCD có đáy là hình vuông vắn ABCD tâm O và có cạnh SA vuông góc với mặt phẳng [ABCD]. Giả sử [α] là mặt phẳng đi qua A và vuông góc với cạnh SC, [α] cắt SC tại I.
a] Xác định giao điểm K của SO với mặt phẳng [α].
b] Chứng minh mặt phẳng [SBD] vuông góc với mặt phẳng [SAC] và BD // [α].
c] Xác định giao tuyến d của mặt phẳng [SBD] và mặt phẳng [α]. Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng [α].
Xem đáp án » 04/05/2022 2,355
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng [CDM] có vuông góc với mặt phẳng [ABN] không? Vì sao?
Xem đáp án » 04/05/2022 2,185
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a] Mặt phẳng [ABCD] vuông góc với mặt phẳng [SBD];
b] Tam giác SBD là tam giác vuông tại S.
Xem đáp án » 04/05/2022 1,875
Tải thêm tài liệu liên quan đến nội dung bài viết Cho tứ diện đều ABCD chứng tỏ AC vuông góc với BD