Kinh Nghiệm Hướng dẫn Select the smallest number by which the number 135000 must be divided to make it a perfect cube 2022
Cao Ngọc đang tìm kiếm từ khóa Select the smallest number by which the number 135000 must be divided to make it a perfect cube được Update vào lúc : 2022-10-09 17:50:35 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.Solution:
Nội dung chính- Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube (i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
Find the smallest number by which [135] must be divided, so that the quotient is a perfect cube.A. $3$B.$5$C.$9$D.$15$
Is divided to make 135 a perfect cube?What is least number by which 135 must be divided to obtain perfect cube?How do you find the smallest number to be divided to get a perfect cube?What is the smallest number by which 6912 must be divided to make it a perfect cube?
A number is a perfect cube only when each factor in the prime factorization is grouped in triples. Using this concept, the smallest number can be identified.
(i) 81

81 = 3 × 3 × 3 × 3
= 33 × 3
Here, the prime factor 3 is not grouped as a triplet. Hence, we divide 81 by 3, so that the obtained number becomes a perfect cube.
Thus, 81 ÷ 3 = 27 = 33 is a perfect cube.
Hence the smallest number by which 81 should be divided to make a perfect cube is 3.
(ii) 128
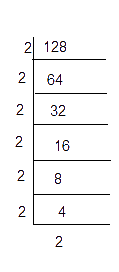
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
= 23 × 23 × 2
Here, the prime factor 2 is not grouped as a triplet. Hence, we divide 128 by 2, so that the obtained number becomes a perfect cube.
Thus, 128 ÷ 2 = 64 = 43 is a perfect cube.
Hence the smallest number by which 128 should be divided to make a perfect cube is 2.
(iii) 135
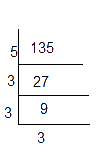
135 = 3 × 3 × 3 × 5
= 33 × 5
Here, the prime factor 5 is not a triplet. Hence, we divide 135 by 5, so that the obtained number becomes a perfect cube.
135 ÷ 5 = 27 = 33 is a perfect cube.
Hence the smallest number by which 135 should be divided to make a perfect cube is 5.
(iv) 192
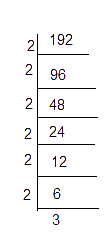
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
= 23 × 23 × 3
Here, the prime factor 3 is not grouped as a triplet. Hence, we divide 192 by 3, so that the obtained number becomes a perfect cube.
192 ÷ 3 = 64 = 43 is a perfect cube
Hence the smallest number by which 192 should be divided to make a perfect cube is 3.
(v) 704

704 = 2 × 2 × 2 × 2 × 2 × 2 × 11
= 23 × 23 × 11
Here, the prime factor 11 is not grouped as a triplet. Hence, we divide 704 by 11, so that the obtained number becomes a perfect cube.
Thus, 704 ÷ 11 = 64 = 43 is a perfect cube
Hence the smallest number by which 704 should be divided to make a perfect cube is 11.
☛ Check: NCERT Solutions for Class 8 Maths Chapter 7
Video Solution:
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube (i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
[embed]https://www.youtube.com/watch?v=FqNogxG_CPc[/embed]
NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.1 Question 3
Summary:
The smallest number by which each of the following numbers must be divided to obtain a perfect cube (i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704 are (i) 3, (ii) 2, (iii) 5, (iv) 3, and (v) 11
☛ Related Questions:
- Which of the following numbers are not perfect cubes?(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656Find the smallest number
by which each of the following numbers must be multiplied to obtain a perfect cube.(i) 243 (ii) 256 (iii) 72 (iv) 675 (v) 100Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?Find the cube root of each of the following numbers by prime factorization method. (i) 64 (ii) 512 (iii) 10648 (iv) 27000 (v) 15625 (vi) 13824 (vii) 110592 (viii) 46656 (ix) 175616 (x) 91125
Find the smallest number by which [135] must be divided, so that the quotient is a perfect cube.A. $3$B.$5$C.$9$D.$15$
Answer
Verified
Hint: We will do prime factorization of 135.Further we will divide 135 to a number, that number is not in triplet form. Then we will convert 135 into a perfect cube.
Complete step by step solution:
Here the given number is $135$
We will use prime factorization method
$3$ $135$ $3$ $45$ $3$ $15$ $5$ $5$ $1$
$135 = 3 times 3 times 3 times 5$
$135 = 3^3 times 5$
Here, one $5$ is left which does not form a triplet
If we divide $135$ by $5$, then it will become a perfect cube.
So, $dfrac1355 = 3^3$
$27 = 3^3$
Hence, the smallest number by which $135$ should be divided to make it a perfect cube is $5$.
Note: In these types of questions usually students get puzzled whether to find HCF or LCM. We note that words like larger, highest etc. are keywords mentioned in the question and they give us ideas to find HCF whereas words like smallest, lowest, least etc. give us direction to find the LCM.
Is divided to make 135 a perfect cube?
Therefore, 135 must be divided by 5 to make it a perfect cube.What is least number by which 135 must be divided to obtain perfect cube?
Hence the smallest number by which 135 should be divided to make a perfect cube is 5.How do you find the smallest number to be divided to get a perfect cube?
Prime factorising 81, we get,. We know, a perfect cube has multiples of 3 as powers of prime factors.. Here, number of 3's is 4.. So we need to divide the factorization by 3 to make 81 a perfect cube.. Hence, the smallest number by which 81 must be divided to obtain a perfect cube is 3..What is the smallest number by which 6912 must be divided to make it a perfect cube?
To do: To find the smallest number by which 6912 must be divided so that the number formed is a perfect cube. Therefore, we should divide 6912 by 22=4 2 2 = 4 , the smallest number to get 1728 which is a cube of 12 . Tải thêm tài liệu liên quan đến nội dung bài viết Select the smallest number by which the number 135000 must be divided to make it a perfect cube