Mẹo What is the smallest number which when divided by 12 16 and 18 gives a remainder of 5 in each case?

Thủ Thuật Hướng dẫn What is the smallest number which when divided by 12 16 and 18 gives a remainder of 5 in each case? Chi Tiết

Hoàng Thị Thanh Mai đang tìm kiếm từ khóa What is the smallest number which when divided by 12 16 and 18 gives a remainder of 5 in each case? được Cập Nhật vào lúc : 2022-10-03 05:26:12 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.

Find the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case.

Nội dung chính

Answer: 95 is the least number which when divided by 6, 15, and 18 leaves a remainder of 5 in each case.Hence, 95 is the least number which when divided by 6, 15, and 18 leaves a remainder of 5 in each case.Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each caseRelated VideosWhat is the smallest number which when divided by 12 and 18 leaves a remainder of 9?What is the least natural number which when divided by 12 and 18?What is the smallest number which when divided by 12 18 and 27 gives a remainder of 5 each time?Which is the least number which when divided by 12 and 16?

Solution

We first find the LCM of 12, 16, 24, and 36 as follows:

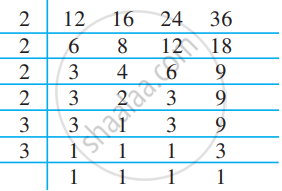
Thus, LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144

144 is the least number which when divided by the given numbers will leave remainder 0 in each case. But we need the least number that leaves remainder 7in each case.
Therefore, the required number is 7 more than 144.

The required least number = 144 + 7 = 151.

Concept: Lowest Common Multiple

Is there an error in this question or solution?

LCM is the smallest positive number that is a multiple of two or more numbers.

Answer: 95 is the least number which when divided by 6, 15, and 18 leaves a remainder of 5 in each case.

To find the least number which when divided by 6, 15, and 18 leaves a remainder of 5 in each case we have to do the following steps:

Find the LCM of 6, 15 and 18Add 5 to the LCM

Explanation:

Below is the LCM shown for 6,15 and 18 using prime factorization.

6 = 2 × 3

15 = 3 × 5

18 = 2 × 3 × 3

Thus, the LCM of 6,15 and 18 = 2 × 3 × 3 × 5 = 90

Now, adding 5 to 90, we get 90 + 5 = 95

Verification:

1) 95/6
Quotient = 15
Remainder = 5

2) 95/15
Quotient = 6
Remainder = 5

3) 95/18
Quotient = 5
Remainder = 5

Hence, 95 is the least number which when divided by 6, 15, and 18 leaves a remainder of 5 in each case.

Solution:

We will be using the concept of LCM(Least Common Multiple) to solve this.

To determine the least number which when divided by 6, 15, and 18 leave the remainder 5 in each case,we need to find the LCM of the three given numbers.

Since, the LCM obtained will be the smallest common multiple of all the three numbers 6, 15, and 18, after getting LCM we need to add 5 to it so as to get 5 as a remainder.

Let's find the LCM of 6, 5 and 18 as shown below.

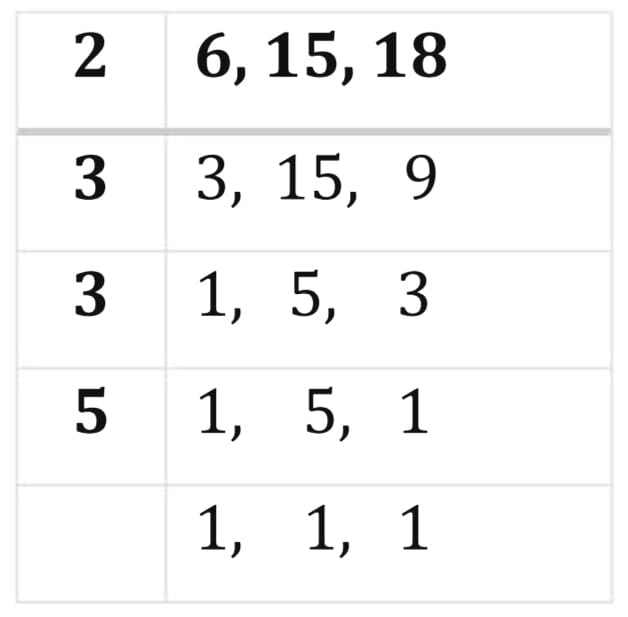
Therefore, LCM of 6, 15 and 18 = 2 × 3 × 3 × 5 = 90.

Thus we can see that, 90 is the least number exactly divisible by 6, 15, and 18.

To get a remainder 5, we need to add 5 to the LCM.

⇒ 90 + 5 = 95.

Thus, when 95 is divided by 6, 15, and 18 we get a remainder of 5 in each case.

Hence, the required number for the given problem is 95.

You can also use the LCM Calculator to solve this.

NCERT Solutions for Class 6 Maths Chapter 3 Exercise 3.7 Question 8

Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case

Summary:

The least number which when divided by 6, 15, and 18 leaving a remainder of 5 in each case will be 95.

☛ Related Questions:

Determine The Smallest 3 Digit Number Which Is Exactly Divisible By 6 8 And 12Determine The Greatest 3 Digit Number Exactly Divisible By 8 10 And 12The Traffic Lights At Three Different Road Crossings Change After Every 48 Seconds 72 Seconds And 108 Seconds Respectively If They Change Simultaneously At 7 Am At What TimeThree Tankers Contain 403 Litres 434 Litres And 465 Litres Of Diesel Respectively Find The Maximum Capacity Of A Container That Can Measure The Diesel Of The Three Containers

The smallest number, which when divided by 12 and 16 leaves remaining 5 and 9 respectively, is :
[A]29
[B]39
[C]41
[D]55

41
Here because, 12 – 5 = 7, 16 – 9 = 7
Since required number = LCM of 12 and 16 – 7
= 48 – 7 = 41.
Hence option [C] is correct answer.

Getting Image
Please Wait...

Course

NCERT

Class 12Class 11Class 10Class 9Class 8Class 7Class 6

IIT JEE

Exam

JEE MAINSJEE ADVANCEDX BOARDSXII BOARDS

NEET

Neet Previous Year (Year Wise)Physics Previous YearChemistry Previous YearBiology Previous YearNeet All Sample PapersSample Papers BiologySample Papers PhysicsSample Papers Chemistry

Download PDF's

Class 12Class 11Class 10Class 9Class 8Class 7Class 6

Exam CornerOnline ClassQuizAsk Doubt on WhatsappSearch DoubtnutEnglish DictionaryToppers TalkBlogJEE Crash CourseAbout UsCareerDownloadGet AppTechnothlon-2022

Logout

+91

trang chủ

English

Class 14

Maths

Chapter

Hcf And Lcm

The least number which when d...

Updated On: 27-06-2022

UPLOAD PHOTO AND GET THE ANSWER NOW!

Text Solution

139144149154

Answer : C

Answer

Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams.

571223276

2.0 K

7.7 K