Thủ Thuật về Nếu tồn tại số h sao cho 2022
Bùi Lam Khê đang tìm kiếm từ khóa Nếu tồn tại số h sao cho được Update vào lúc : 2022-11-22 22:38:05 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.I. KHÁI NIỆM CỰC ĐẠI, CỰC TIỂU
Cho hàm số (y=fleft(xright)) xác định và liên tục trên khoảng chừng (left(a;bright)) (hoàn toàn có thể (a) là (-infty), (b) là (+infty)) và điểm (x_0inleft(a;bright)).
Nội dung chính Show- I. KHÁI NIỆM CỰC ĐẠI, CỰC TIỂUII. ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊIII. QUY TẮC TÌM CỰC TRỊ
a) Nếu tồn tại số (h>0) sao cho (fleft(xright)< fleft(x_0right)) với mọi (xinleft(x_0-h;x_0+hright)) và (xne x_0) thì ta nói hàm số (fleft(xright)) đạt cực lớn tại (x_0).
b) Nếu tồn tại số (h>0) sao cho (fleft(xright)>fleft(x_0right)) với mọi (xinleft(x_0-h;x_0+hright)) và (xne x_0) thì ta nói hàm số (fleft(xright)) đạt cực tiểu tại (x_0).
Chú ý:
1. Nếu hàm số (fleft(xright)) đạt cực lớn (cực tiểu) tại (x_0) thì (x_0) được gọi là vấn đề cực lớn (điểm cực tiểu) của hàm số, (fleft(x_0right)) được gọi là giá trị cực lớn (giá trị cực tiểu) của hàm số, kí hiệu là (f_CĐleft(f_CTright)), còn điểm (Mleft(x_0;fleft(x_0right)right)) được gọi là vấn đề cực lớn (điểm cực tiểu) của đồ thị hàm số.
2. Các điểm cực lớn và cực tiểu được gọi chung là những điểm cực trị. Giá trị cực lớn (giá trị cực tiểu) còn được gọi là cực lớn (cực tiểu) và được gọi chung là cực trị của hàm số.
3. Dễ dàng chứng tỏ được rằng, nếu hàm số (y=fleft(xright)) có đạo hàm trên khoảng chừng (left(a;bright)) và đạt cực lớn hoặc cực tiểu tại (x_0) thì (f'left(x_0right)=0).
II. ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ
Định lí 1:
Giả sử hàm số (y=fleft(xright)) liên tục trên khoảng chừng (K=left(x_0-h;x_0+hright)) và có đạo hàm trên (K) hoặc trên (K)\(leftx_0right\), với (h>0).
a) Nếu (f'left(xright)>0) trên khoảng chừng (left(x_0-h;x_0right)) và (f'left(xright)< 0) trên khoảng chừng (left(x_0;x_0+hright)) thì (x_0) là một điểm cực lớn của hàm số (fleft(xright)).
b) Nếu (f'left(xright)< 0) trên khoảng chừng (left(x_0-h;x_0right)) và (f'left(xright)>0) trên khoảng chừng (left(x_0;x_0+hright)) thì (x_0) là một điểm cực tiểu của hàm số (fleft(xright)).

Ví dụ 1: Tìm những điểm cực trị của đồ thị hàm số (fleft(xright)=-x^2+1).
Giải:
Hàm số xác định với mọi (xin R).
Ta có (f'left(xright)=-2x) , (f'left(xright)=0Leftrightarrow x=0). Bảng biến thiên:

Từ bảng biến thiên suy ra (x=0) là vấn đề cực lớn của hàm số và đồ thị hàm số có một điểm cực lớn là (left(0;1right)).

Ví dụ 2: Tìm những điểm cực trị của hàm số (y=x^3-x^2-x+3).
Giải:
Hàm số xác định với mọi (xin R).
Ta có (y'=3x^2-2x-1) ; (y'=0Leftrightarrowleft[beginmatrixx=1\x=-dfrac13endmatrixright.). Bảng biến thiên:
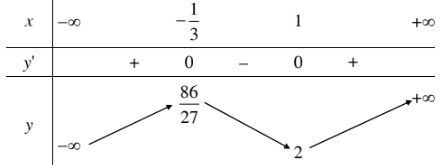
Từ bảng biến thiên ta suy ra (x=-dfrac13) là vấn đề cực lớn, (x=1) là vấn đề cực tiểu của hàm số.
Ví dụ 3: Tìm cực trị của hàm số (y=dfrac3x+1x+1).
Giải:
Hàm số xác định tại mọi (xne-1)
Ta có (y'=dfrac2left(x+1right)^2>0,forall xne-1) . Vậy hàm số đã cho không còn cực trị.
III. QUY TẮC TÌM CỰC TRỊ
Từ định lí 1 ta có Quy tắc 1:
1. Tìm tập xác định.
2. Tính (f'left(xright)). Tìm những điểm tại đó (f'left(xright)=0) hoặc (f'left(xright)) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra những điểm cực trị.
Định lí 2:
GIả sử hàm số (y=fleft(xright)) có đạo hàm cấp hai trong khoảng chừng (left(x_0-h;x_0+hright)) với (h>0). Khi đó:
a) Nếu (f'left(x_0right)=0,f''left(x_0right)>0) thì (x_0) là vấn đề cực tiểu;
b) Nếu (f'left(x_0right)=0,f''left(x_0right)< 0) thì (x_0) là vấn đề cực lớn.
Áp dụng định lí 2, ta có Quy tắc 2:
1. Tìm tập xác định.
2. Tính (f'left(xright)). Giải phương trình (f'left(xright)=0) và kí hiệu (x_ileft(i=1,2,...,nright)) là những nghiệm của nó.
3. Tính (f''left(xright)) và (f''left(x_iright)).
4. Dựa vào dấu của (f''left(x_iright)) suy ra tính chất cực trị của điểm (x_i).
Ví dụ 4. Tìm cực trị của hàm số (fleft(xright)=dfracx^44-2x^2+6).
Giải:
Hàm số xác định với mọi (xin R).
(f'left(xright)=x^3-4x=xleft(x^2-4right)) , (f'left(xright)=0Rightarrow x_1=0,x_2=-2,x_3=2)
(f''left(xright)=3x^2-4)
(f''left(pm2right)=8>0Rightarrow x=-2) và (x=2) là hai điểm cực tiểu;
(f''left(0right)=-4< 0Rightarrow x=0) là vấn đề cực lớn.
Kết luận: (fleft(xright)) đạt cực tiểu tại (x=-2) và (x=2), (f_CT=fleft(pm2right)=2)
(fleft(xright)) đạt cực lớn tại (x=0) và (f_CĐ=fleft(0right)=6).
Ví dụ 5: Tìm những điểm cực trị của hàm số (fleft(xright)=sin2x).
Giải:
Hàm số xác định với mọi (xin R).
(f'left(xright)=2cos2x,f'left(xright)=0Leftrightarrow2x=dfracpi2+lpiLeftrightarrow x=dfracpi4+ldfracpi2left(lin Zright))
(f''left(xright)=-4sin2x)
(f''left(dfracpi4+ldfracpi2right)=-4sinleft(dfracpi2+lpiright)=left{beginmatrix-4left(l=2kright)\4left(l=2k+1right)endmatrixright.left(lin Zright))
Kết luận: (x=dfracpi4+kpileft(kin Zright)) là những điểm cực lớn của hàm số;
(x=dfrac3pi4+kpileft(kin Zright)) là những điểm cực tiểu của hàm số.
Danh sách những phiên bản khác của bài học kinh nghiệm tay nghề này. Xem hướng dẫn
Tải thêm tài liệu liên quan đến nội dung bài viết Nếu tồn tại số h sao cho