Mẹo Hướng dẫn Cho tam giác ABC đều nội tiếp đường tròn (O điểm M trên cung nhỏ AC) 2022
Họ tên bố (mẹ) đang tìm kiếm từ khóa Cho tam giác ABC đều nội tiếp đường tròn (O điểm M trên cung nhỏ AC) được Update vào lúc : 2022-11-13 00:26:08 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Ôn tập chương 3 – Hình học 9 – Bài 3 trang 113 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung nhỏ AC lấy một điểm D. Trên dây
Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung nhỏ AC lấy một điểm D. Trên dây cung BD lấy điểm M sao cho DM = DC.
a) Chứng minh MCD là tam giác đều.
b) Khi điểm D di động trên cung nhỏ AC (D hoàn toàn có thể trùng điểm A hoặc điểm C), tập hợp những điểm M là gì?
a) Chứng minh tam giác MCD là tam giác cân có một góc bằng 600.
b) Chứng minh (widehat BOC = 120^0) không đổi.
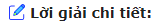
Quảng cáo - Advertisements
a) Ta có: (widehat CDM = widehat CAB = 60^0) (2 góc nội tiếp cùng chắn cung BC).
Xét tam giác MCD có: (left{ beginarraylMC = MD,,left( gt right)\widehat CDM = 60^0,left( cmt right)endarray right. Rightarrow Delta MCD) đều.
b) Do tam giác MCD đều (cmt) ( Rightarrow widehat CMD = 60^0).
Mà (widehat CMD + widehat BMC = 180^0) (2 góc kề bù) ( Rightarrow widehat BMC = 180^0 – widehat CMD = 180^0 – 60^0 = 120^0).
B, C cố định và thắt chặt, do đó M thuộc cung chứa góc 1200 dựng trên đoạn thẳng BC.
Giới hạn: Khi (D equiv B Rightarrow M equiv B;,,D equiv C Rightarrow M equiv C).
Vậy tập hợp những điểm M là cung chứa góc 1200 dựng trên đoạn thẳng BC cùng phía với điểm A.

Khách
Hãy nhập thắc mắc của bạn vào đây
Dưới đây là một vài thắc mắc hoàn toàn có thể liên quan tới thắc mắc mà bạn trình lên. Có thể trong đó có câu vấn đáp mà bạn cần!
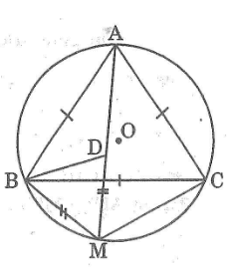
Ta có: ∆ABD = ∆CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Cho đường tròn (O) và hai dây AB,AC bằng nhau.Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròng (O) ở E. Chứng minh rằng : AB2= AD.AE
Xem đáp án » 04/05/2022 5,023
Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn (O). Các đường phân giác của hai góc B và C cắt nhau ở E và cắt đường tròn lần lượt tại F và D. Chứng minh rằng tứ giác EDAF là một hình thoi
Xem đáp án » 04/05/2022 2,960
Cho đường tròn (O) và một điểm M cố định và thắt chặt không nằm trên đường tròn .Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B.Chứng minh rằng tích MA.MB không đổi
Xem đáp án » 04/05/2022 2,346
Cho đường tròn (O) và hai tuyến đường kính AB,CD vuông góc với nhau.Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến với đường tròn (O) tại M.Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng ∠MSD = 2.MBA
Xem đáp án » 04/05/2022 2,339
Cho tam giác ABC nội tiếp trong đường tròn tâm O, biết góc A = 32°, góc B = 84°. Lấy những điểm D, E, F thuộc đường tròn (O) sao cho AD = AB, BE = BC, CF = CA . Hãy tính những góc của tam giác DEF
Xem đáp án » 04/05/2022 1,595
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E. Chứng minh CD song song với AB.
Xem đáp án » 04/05/2022 1,483
Đã gửi 11-02-2014 - 23:38
a)Trên tia MA lấy điểm I sao cho MI=MC
Dễ thấy $Delta CIM$ đều $Rightarrow MC=CI$
Xét 2 tam giác $Delta AIC$$ và Delta BMC$ có
$IC=MC$
$angle IAC=angle MCB$ (vì cùng cộng với $angle BCI = 60^circ$)
$AC=BC$
Do đó $Delta AIC$ = $Delta BMC$
$Rightarrow AI=BM$
$Rightarrow$ Đpcm
b) Dễ thấy $$Delta BAM sim Delta DCM$$ (g.g)
nên $fracAMCM=fracBMDMRightarrow AM.DM=CM.BM$
$Rightarrow fracAMBM.CM=frac1MD$
Áp dụng kết quả câu (a) ta có đpcm
c) Đặt MA=x, MB=y. Ta có
$AM^2+BM^2+CM^2=x^2+y^2+(x-y)^2=2(x^2+y^2-xy)$ (1)
Kẻ $BH$ vuông góc với $AM$
Do $angle BMH =60^circ$ nên $MH = fracy2, BH^2=y^2-(fracy2)^2=frac3y^24$
do đó $AB^2=AH^2+BH^2=x^2+y^2-xy$ (2)
Từ (1) và (2) $Rightarrow MA^2+ MB^2+MC^2=2AB^2$ mà $Delta ABC$ đều
nên $AB=Rsqrt3$
$Rightarrow$ Đpcm
Bài viết đã được sửa đổi nội dung bởi Pham Le Yen Nhi: 12-02-2014 - 00:03
- lý thuyết
trắc nghiệm
hỏi đáp
bài tập sgk
Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm của cung nhỏ BC. Trên MA lấy điểm D sao cho MD = MB.
a) Hỏi tam giác MBD là tam giác gì ?
b) So sánh tam giác BDA và BMC
c) Chứng minh rằng MA = MB + MC
Các thắc mắc tương tự
Chọn xác định đúng. Góc ở tâm là góc
Chọn xác định đúng. Trong một đường tròn, số đo cung nhỏ bằng
Tải thêm tài liệu liên quan đến nội dung bài viết Cho tam giác ABC đều nội tiếp đường tròn (O điểm M trên cung nhỏ AC)
