Kinh Nghiệm Hướng dẫn Bề lõm của parabol là gì 2022
Hoàng Lê Minh Long đang tìm kiếm từ khóa Bề lõm của parabol là gì được Cập Nhật vào lúc : 2022-12-19 19:28:05 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.Parabol là gì ? Bạn đã nắm bắt được những thông tin, nội dung nào liên quan đến đường Parabol rồi ? Cùng chúng tôi mày mò và tìm hiểu những nội dung về chủ đề này dưới nội dung bài viết này nhé !
Nội dung chính Show- Parabol là gì ? Parabol có dạng gì ? Cách lập phương trình Parabol Hướng dẫn cách vẽ Parabol cho hàm số bậc 21. Lý thuyết chung về hàm số bậc 2 lớp 101.1. Định nghĩa 1.2. Chiều biến thiên và bảng biến thiên2.1. Cách vẽ đồ thị hàm số bậc 22.2. Bài tập ví dụ vẽ đồ thị hàm số bậc 2
Tham khảo nội dung bài viết khác:
- Định lý Vi-et trong phương trình bậc 2, bậc 3, bậc 4 Toán Lớp 9Tính giá trị biểu thức lớp 3 từ cơ bản đến nâng cao của Học Kỳ 2
Parabol là gì ?
Parabol là một đường conic được tạo bởi giao của một hình nón và một mặt phẳng song song với đường sinh của hình đó. Một parabol cũng luôn có thể có thế được định nghĩa như một tập hợp những điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
Parabol có dạng gì ?
– Đường parabol là đồ thị của hàm số bậc 2 có dạng: y = ax^2 + bx + c.
– Dạng tổng quát của một phương trình parabol là:
( Ax + By )^2 + Cx + Dy + E = 0
==> được rút ra từ phương trình tổng quát của những đường conic và tính chất của parabol B^2 = 4 AC
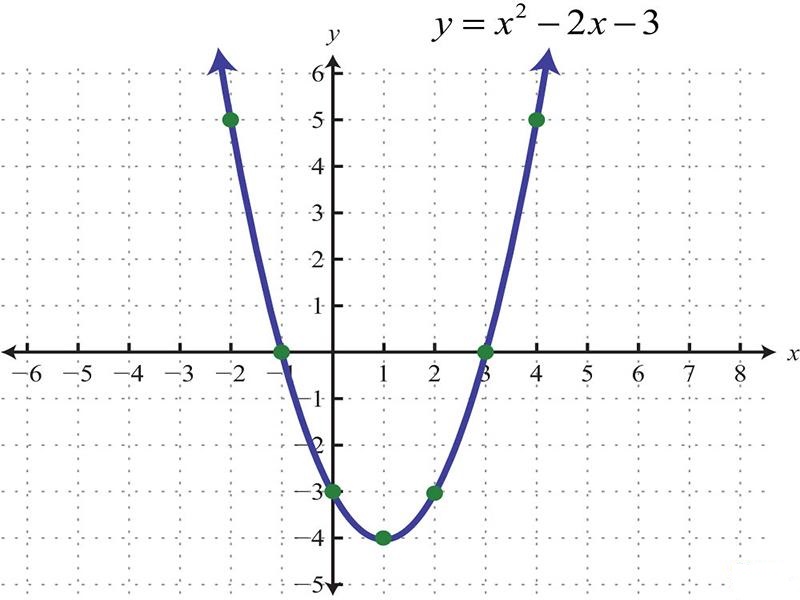
Cách lập phương trình Parabol
– Cho hàm số y = ax^2. Hàm số này xác định trên R :
+) Nếu a > 0 thì hàm số giảm trên (-∞ ; 0) ; tăng trên (0;+ ∞ ),đạt cực tiểu khi x = 0
+) Nếu a < 0 thì hàm số tăng trên (-∞; 0) ;giảm trên (0;+ ∞ ).đạt cực lớn khi x = 0
+) Đồ thị Parabol của hàm số y = ax^ 2 có đỉnh là gốc O và trục đối xứng là Oy.
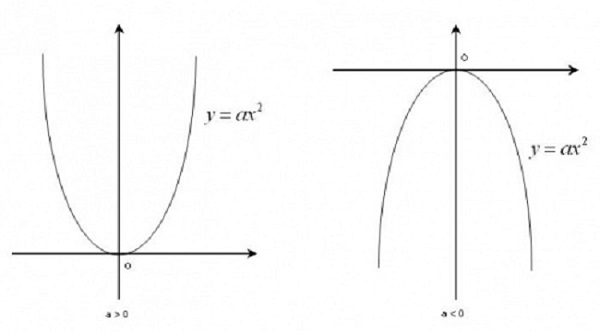
Hướng dẫn cách vẽ Parabol cho hàm số bậc 2
– Để vẽ parabol y=ax^2 + bx + c (a≠0), ta thực hiện tiến trình sau:
+) Bước 1: Xác định tọa độ của đỉnh I(−b/2a;−Δ/4a)
+) Bước 2: Vẽ trục đối xứng x=−b/2a.
+) Bước 3: Xác định tọa độ những giao điểm của parabol với trục tung ( điểm (0;c) ) và trục hoành (nếu có).
+) Bước 4: Vẽ parabol: Chú ý đến dấu của thông số a.
Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
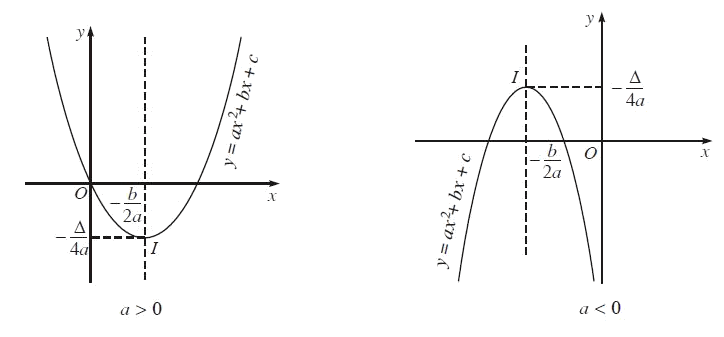
Cám ơn bạn đã theo dõi nội dung bài viết này của chúng tôi, kỳ vọng những nội dung trong nội dung bài viết chúng tôi chia sẻ sẽ đem đến những nội dung hữu ích nhất giành cho bạn nhé !
- Nếu (aTrong chương trình Đại số lớp 10, đồ thị hàm số bậc 2 là phần kiến thức và kỹ năng rất quan trọng. Trong nội dung bài viết này, VUIHOC sẽ ra mắt tới những em học viên lý thuyết chung về hàm số bậc 2 trong chương trình Toán THPT lớp 10 cùng với bộ 20 thắc mắc rèn luyện tinh lọc.
1. Lý thuyết chung về hàm số bậc 2 lớp 10
Trước khi tìm hiểu về đồ thị hàm số bậc 2, những em học viên cần nắm vững những kiến thức và kỹ năng nền tảng của hàm số bậc hai như định nghĩa và chiều biến thiên trước tiên.
1.1. Định nghĩa
Hàm số bậc hai lớp 10 được định nghĩa là dạng hàm số có công thức tổng quát là $y=ax^2+bx+c$, trong đó a,b,c là hằng số cho trước, $aneq 0$.
Tập xác định của hàm số bậc hai lớp 10 là: $D=mathbbR$
Biệt thức Delta: $Delta =b^2-4ac$
1.2. Chiều biến thiên và bảng biến thiên
Xét chiều biến thiên và bảng biến thiên là bước rất quan trọng để vẽ được đồ thị hàm số bậc 2. Cho hàm số bậc 2 $y=ax^2+bx+c$ với $a>0$, chiều biến thiên của hàm só bậc hai lớp 10 khi đó là:
Đồng biến trên khoảng chừng $(frac-b2a;+infty )$
Nghịch biến trên khoảng chừng $(-infty ;frac-b2a)$
Giá trị cực tiểu của hàm số bậc hai lớp 10 đạt tại $(frac-b2a; frac-Delta 4a)$. Khi đó, giá trị nhỏ nhất của hàm số là $frac-Delta 4a$ tại $x=frac-b2a$.
Cho hàm số $y=ax^2+bx+c$ với $a<0$, chiều biến thiên khi đó là:
Đồng biến trên khoảng chừng $(-infty ;frac-b2a)$
Nghịch biến trên khoảng chừng $(frac-b2a;+infty )$
Giá trị cực lớn của hàm số bậc 2 đạt tại $(frac-b2a; frac-Delta 4a)$. Khi đó giá trị lớn số 1 của hàm số là $frac-Delta 4a$ tại $x=frac-b2a$.
Sau khi xét được chiều biến thiên, ta hoàn toàn có thể vẽ được bảng biến thiên như sau:
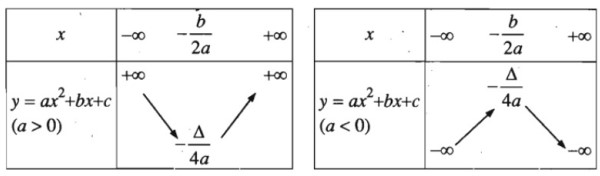
2. Đồ thị hàm số bậc 2 có dạng ra làm sao?
2.1. Cách vẽ đồ thị hàm số bậc 2
Để vẽ đồ thị hàm số bậc 2, những em học viên hoàn toàn có thể tuỳ theo từng trường hợp để sử dụng 1 trong 2 cách sau đây.
Cách 1 (cách này hoàn toàn có thể dùng cho mọi trường hợp):
Bước 1: Xác định toạ độ đỉnh I
Bước 2: Vẽ trục đối xứng của đồ thị
Bước 3: Xác định toạ độ những giao điểm của Parabol lần lượt với trục tung và trục hoành (nếu có).
Cách 2 (sử dụng cách này khi đồ thị hàm số có dạng $y=ax^2$)
Đồ thị hàm số bậc 2 $y=ax^2+bx+c (aneq 0)$ được suy ra từ đồ thị hàm $y=ax^2$ bằng phương pháp:
Nếu $fracb2a>0$ thì tịnh tiến song song với trục hoành $fracb2a$ đơn vị về phía bên trái, về bên phải nếu $fracb2a<0$.
Nếu $frac-Delta 4a>0$ thì tịnh tiến song song với trục tung $-left |fracDelta 4a right |$ đơn vị lên trên, xuống dưới nếu $frac-Delta 4a<0$.
Đồ thị hàm số $y=ax^2+bx+c (aneq 0)$ có dạng như sau:
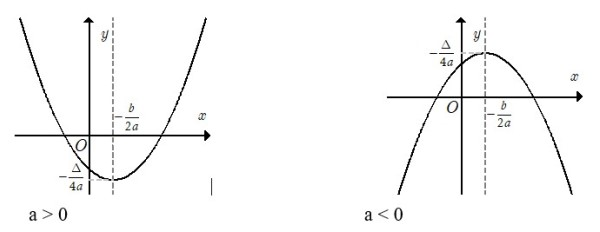
Đồ thị hàm số bậc hai lớp 10 $y=ax^2+bx+c (aneq 0)$ có đặc điểm là đường parabol với:
Đỉnh: $I(frac-b2a;frac-Delta 4a)$
Trục đối xứng: đường thẳng $x=frac-b2a$
Nếu $a>0$, phần lõm của parabol quay lên trên; Nếu $a<0$, phần lõm của parabol quay xuống dưới.
Giao điểm với trục tung: $A(0;c)$
Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình $ax^2+bx+c=0$.
Lưu ý: Để vẽ đồ thị hàm số bậc 2 chứa trị tuyệt đối $y=ax^2+bx+c$ ta tuân theo tiến trình sau:
Trước hết ta vẽ đồ thị $(P): ax^2+bx+c$
Ta có:
Vậy đồ thị hàm số $y=ax^2+bx+c$ gồm có 2 phần:
Phần 1: Chính là đồ thị hàm số bậc 2 (P) lấy phần phái trên trục Ox.
Phần 2: Lấy đối xứng phần đồ thị (P) phía dưới trục Ox qua trục Ox.
Vẽ đồ thị hàm số $(P_1)$ và $(P_2)$, ta được đồ thị hàm số bậc 2 $y=ax^2+bx+c$.
2.2. Bài tập ví dụ vẽ đồ thị hàm số bậc 2
Ví dụ 1: Vẽ đồ thị của hàm số bậc 2 $y=x^2+3x+2$
Hướng dẫn giải:
Ta có:
Bảng biến thiên của hàm số:
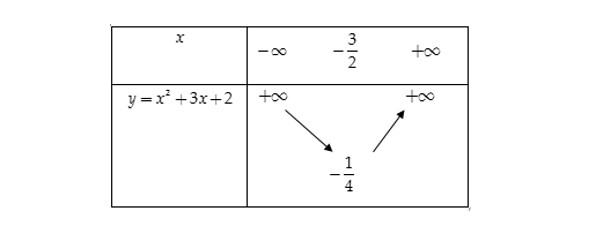
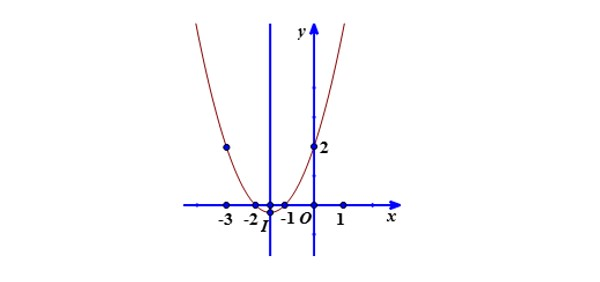
Vậy ta hoàn toàn có thể suy ra: Đồ thị hàm số $y=x^2+3x+2$ có đỉnh I(-3/2;-¼) và đi qua những điểm A(-2;0), B(-1;0), C(0;2), D(-3;2).
Đồ thị hàm số $y=x^2+3x+2$ nhận đường x=-3/2 làm trục đối xứng và có phần lõm hướng lên trên.
Ví dụ 2 (Luyện tập 2 trang 41 Toán lớp 10 tập 1): Vẽ đồ thị mỗi hàm số bậc hai sau:
a) $y=x^2–4x–3$
b) $y=x^2+2x+1$
Hướng dẫn giải:
a) $y=x^2–4x–3$
Ta có: $a=1, b=-4, c=-3, =(-4)^2-4.1.(-3)=28$.
Toạ độ đỉnh: I(2;-7)
Trục đối xứng: $x=2$
Giao điểm của parabol với trục tung: A(0;-3)
Giao điểm của parabol với trục hoành: B(2-7;0) và C(2+7;0)
Điểm đối xứng với A(0;-3) qua trục x=2 là D(4;-3)
Vì a>0 nên phần lõm của đồ thị hướng lên trên.
Đồ thị của hàm số bậc 2 lớp 10 $y=x^2–4x–3$ có dạng như sau:
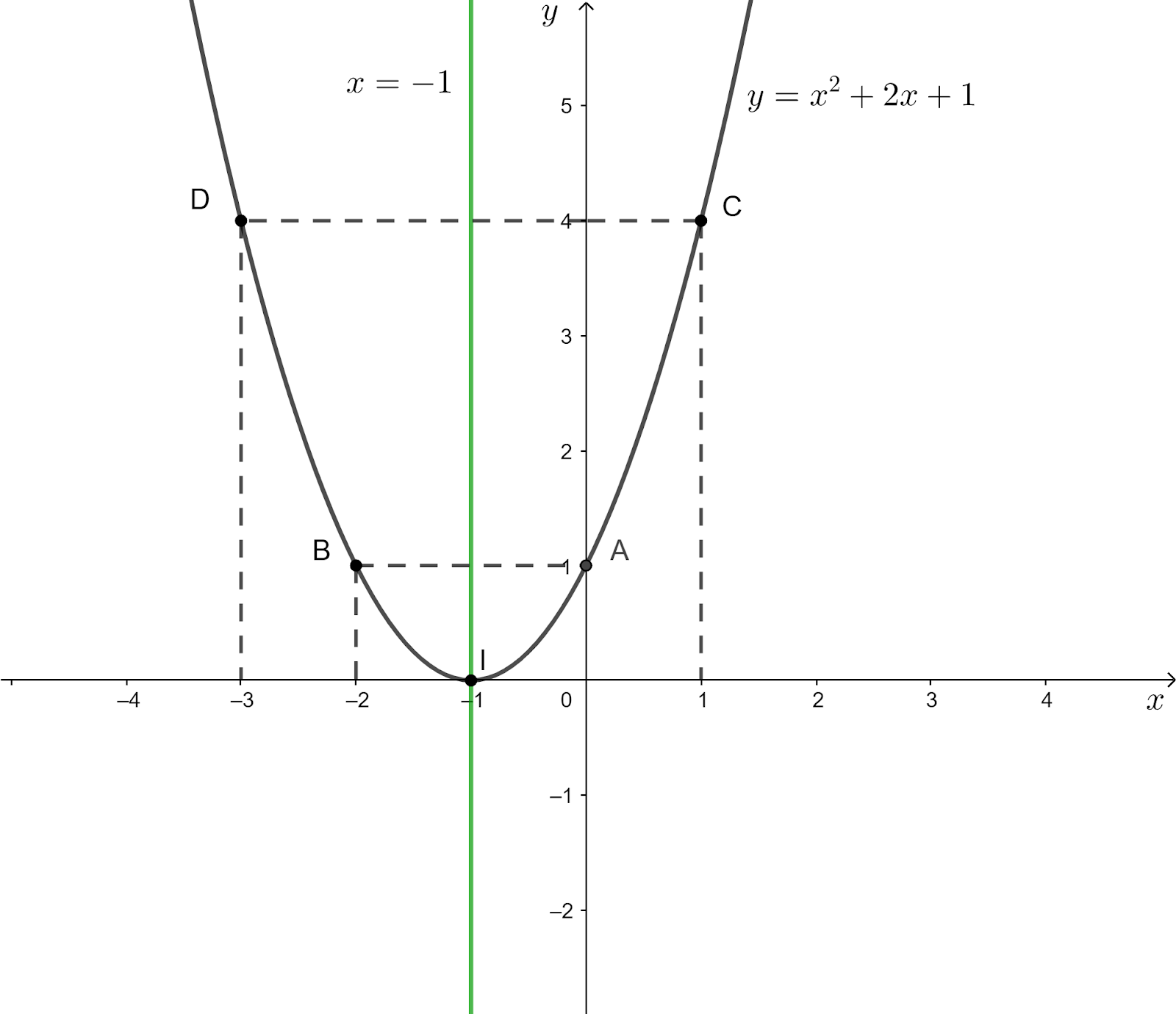
b) $y=x^2+2x+1$
Ta có: a=1; b=2; c=1; =$2^2-4.1+1=0$
Toạ độ đỉnh: I(-1;0)
Trục đối xứng: x=-1
Giao điểm của parabol với trục tung là A(0;1)
Giao điểm của parabol với trục hoành đó đó là đỉnh I.
Điểm đối xứng với A(0;1) qua trục đối xứng x=-1 là B(-2;0)
Lấy điểm C(1;4) thuộc đồ thị hàm số đề bài, điểm đối xứng C qua trục x=-1 là vấn đề D(-3;4)
Vì a>0 nên phần lõi của đồ thị hướng lên phía trên.
Đồ thị hàm số $y=x^2+2x+1$ có dạng sau đây:
Ví dụ 3: Lập bảng biến thiên và vẽ đồ thị hàm số bậc 2 sau:
$y=x^2-3x+2$
$y=-2x^2+4$
Hướng dẫn giải:
Ta có:
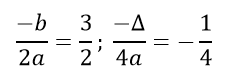
Bảng biến thiên:
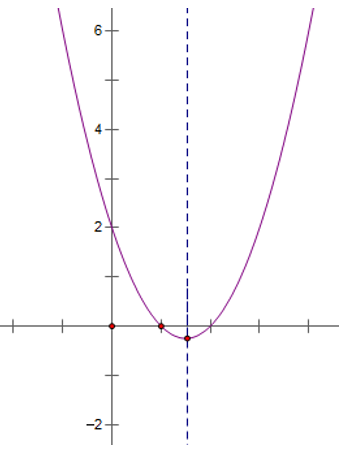
Xét thấy, đồ thị hàm số $y=x^2-3x+2$ có đỉnh là I(3/2; -1/4), đi qua những điểm A(2; 0); B (1; 0), C(0; 2).
Suy ra, đồ thị hàm số nhận đường $x=frac32$ làm trục đối xứng và có bề lõm hướng lên trên.
Đồ thị hàm số bậc 2 $y=x^2-3x+2$ có hình dạng như sau:
Ta có:
Bảng biến thiên:
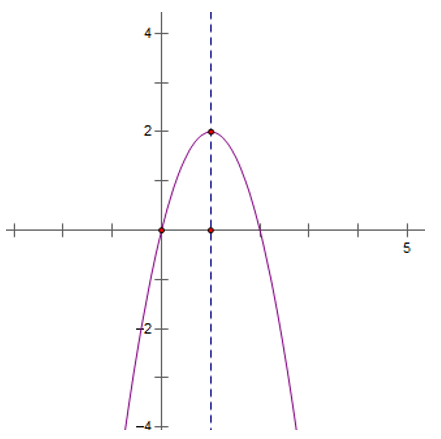
Xét thấy, đồ thị hàm số có $y=-2x^2+4x$ nhận I(1;2) là đỉnh, đi qua những điểm O(0;0), B(2;0).
Suy ra, đồ thị hàm số nhận đường x=1 làm trục đối xứng và có bề lõm hướng xuống dưới.
3. Luyện tập vẽ đồ thị hàm số bậc 2
Để rèn luyện thành thạo những dạng bài tập về đồ thị hàm số bậc 2, những em học viên cùng VUIHOC thực hành với bộ thắc mắc trắc nghiệm sau đây nhé!
Câu 1: Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?
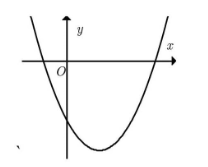
A. $a>0, b<0, c<0$
B. $a>0, b<0, c>0$
C. $a>0, b>0, c>0$
D. $a<0, b<0, c<0$
Câu 2: Parabol $y=-x^2+2x+3$ có phương trình trục đối xứng là:
A. x=-1
B. x=2
C. x=1
D. x=-2
Câu 3: Cho hàm số $y=x^2-2x-1$. Mệnh đề nào dưới đây là sai?
Câu 4: Parabol $(P):y=-2x^2-6x+3$ có hoành độ đỉnh bằng bao nhiêu?
Câu 5: Viết phương trình trục đối xứng của đồ thị hàm số bậc 2 $y=x^2-2x+4$
Câu 6: Trục đối xứng của parabol $y=2x^2+2x-1$ là đường thẳng có phương trình:
Câu 7: Toạ độ đỉnh I của parabol $y=x^2-2x+7$ là:
Câu 8: Cho parabol $(P):y=3x^2-2x+1$. Điểm nào sau đây là đỉnh của (P)?
Câu 9: Cho hàm số bậc hai $y=ax^2+bx+c (aneq 0)$ có đồ thị hàm số bậc 2 (P), đỉnh của (P) được xác định bởi công thức nào sau đây?
Câu 10: Cho hàm số $y=ax^2+bx+c (a>0)$. Khẳng định nào sau đây là sai?
Câu 11: Cho hàm số $y=(m-1)x^2-2(m-2)x+m-3 (mneq 1)$ (P). Đỉnh của (P) là $S(-1;-2)$ thì m bằng bao nhiêu?
Câu 12: Đồ thị phía dưới là đồ thị của hàm số nào?
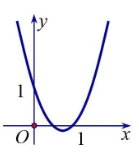
A.$y=-2x^2+3x-1$
B.$y=-x^2+3x-1$
C.$y=2x^2-3x+1$
D.$y=x^2-3x+1$
Câu 13: Đồ thị hình phía dưới là đồ thị của hàm số nào?
Câu 14: Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình vẽ sau đây, dấu những thông số của hàm số đó là:
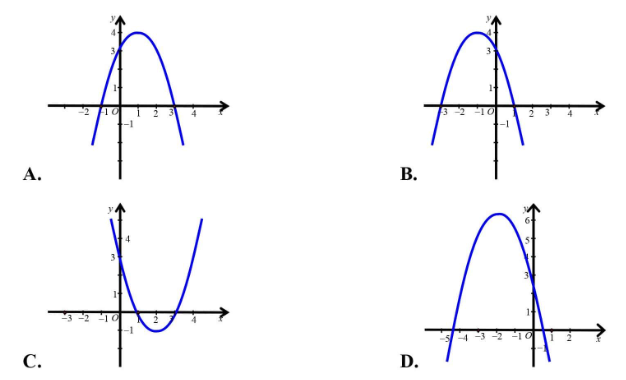
Câu 15: Hàm số $y=-x^2+2x+3$ có đồ thị là hình nào trong những hình sau đây?
Câu 16: Hàm số nào sau đây có đồ thị như hình?
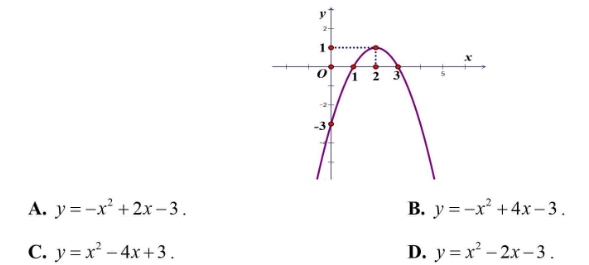
Câu 17: Hàm số nào sau đây có đồ thị như hình?
Câu 18: Đồ thị hàm số bậc 2: $y=x^2-6x+5$
Câu 19: Hàm số $y=ax^2+bx+c$ có đồ thị như hình vẽ sau. Mệnh đề nào dưới đây là đúng?
Câu 20: Cho đồ thị hàm số bậc 2 dạng parabol (P): $y=ax^2+bx+c (aneq 0)$ có đồ thị như hình dưới. Tìm những giá trị m để phương trình $ax^2+bx+c=m$ có 4 nghiệm phân biệt.
Hướng dẫn giải rõ ràng
Câu 1:
Chọn A.
Parabol có bề lõm quay lên trên => $a>0$. Loại D.
Parabol cắt trục tung tại điểm có tung độ âm nên $c<0$. Loại B, C.
Câu 2:
Chọn C.
Parabol $y=-x^2+2x+3$ có trục đối xứng là đường thẳng $x=frac-b2a$ => $x=1$.
Câu 3:
Chọn D.
Trục đối xứng của đồ thị hàm số là đường thẳng $x=frac-b2a=1$.
Câu 4:
Chọn A
Hoành độ đỉnh của parabol (P) được tính như sau:
Câu 5:
Chọn A.
Đồ thị hàm số $y=ax^2+bx+c$ với $aneq 0$ có trục đối xứng là đường thẳng có phương trình x=-b/2a
Vậy đồ thị hàm số $y=x^2-2x+4$ có trục đối xứng là đường thẳng phương trình x=1.
Câu 6:
Chọn D.
Phương trình của trục đối xứng là x=-2/2.2=-½
Câu 7:
Chọn B.
Câu 8:
Chọn B.
Câu 9:
Chọn A.
Đỉnh của parabol $(P): ax^2+bx+c (aneq 0)$ là vấn đề:
Câu 10:
Chọn B.
Dựa bào biến thiên của hàm số $y=ax^2+bx+c (a>0)$ ta thấy những xác định A, C, D đúng.
Khẳng định B là sai vì có những hàm số bậc hai không cắt trục hoành như hàm số $y=-2x^2+3x-9/8$
Câu 11:
Chọn A.
Do đỉnh của (P) là S(-1;-2) nên ta có:
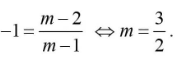
Câu 12:
Chọn C.
Đồ thị cắt trục tung tại điểm có tung độ bằng 1.
Đồ thị cắt trục hoành tại điểm có hoành độ bằng 1, phương trình hoành độ giao điểm phải có nghiệm x=1, ta có phương trình sau đây:
Câu 13:
Chọn B.
Do bề lõm của đồ thị hướng lên trên nên a>0 => Loại đáp án C, D.
Đồ thị giao trục Ox tại điểm (1;0) và (½; 0) =>< Loại A.
Câu 14:
Chọn B.
Đồ thị là parabol có bề lõm hướng xuống dưới nên $a<0$.
Đồ thị cắt chiều dương của trục Oy nên $c>0$.
Trục đối xứng $x=-b/2a>0$, mà $a<0$, nên $b>0$.
Câu 15:
Chọn A.
Do $a=-1$ nên đồ thị có dạng lõm xuống dưới => Loại C
Tính toán được đỉnh của đồ thị có toạ độ $I (1;4)$
Câu 16:
Chọn B.
Quan sát đồ thị ta loại đáp án A và D. Phần đồ thị bên phải trục tung là đồ thị (P) của hàm số $y=-x^2+5x-3$ với $x>0$, toạ độ đỉnh của (P) là (5/2; 13/4), trục đối xứng là x=2,5. Phần đồ thị bên trái trục tung là vì lấy đối xứng phần đồ thị bên phải của (P) qua trục tung Oy. Ta được cả hai phần là đồ thị của hàm số $y=-x^2+5x-3$.
Câu 17:
Chọn B.
Dựa vào đồ thị ta suy được a<0 và hoành độ đỉnh là 2.
$y=-x^2+4x-3 => a=-1; I(2;1)$.
Câu 18:
Chọn D.
Đồ thị © của hàm số $y=x^2-6x+5$ gồm 2 phần:
Phần đồ thị $(C_1)$: là phần đồ thị của hàm số $y_1=x^2-6x+5$ nằm bên phải trục tung.
Phần đồ thị $(C_2)$: là phần đô fthij của hàm số $y_2=x^2-6x+5$ đã có được bằng phương pháp lấy đối xứng phần đồ thị $(C_1)$ qua trục tung.
Ta có đồ thị © có dạng như hình vẽ dưới đây:
Kết luận đồ thị C) có trục đối xứng phương trình x=0.
Câu 19:
Chọn D.
Quan sát đồ thị, ta thấy:
Đồ thị quay bề lõm xuống dưới nên $a<0$; Hoành độ đỉnh $x_1=frac-b2a>0 b/a<0$ => $b>0$.
Ta có: Đồ thị cắt Ox tại điểm có tung độ âm nên $c<0$.
Vậy $a<0, b>0,c<0$.
Câu 20:
Chọn B.
Quan sát đồ thị ta có đỉnh của parabol là $I(2;3)$ nên:
Mặt khác (P) cắt trục tung tại $(0;-1)$ nên $c=-1$. Suy ra:
$(P):y=-x^2+4x-1$ suy ra hàm số $y=-x^2+4x-1$ có đồ thị là phần hình phía trên trục hoành của (P) và phần đã có được do lấy đối xứng phần dưới trục hoành của (P), như hình vẽ:
Phương trình $ax^2+bx+c=m$ hay $-x^2+4x-1=m$ có 4 nghiệm phân biệt khi đường thẳng $y=m$ cắt đồ thị hàm số bậc 2 $y=-x^2+4x-1$ tại 4 điểm phân biệt.
kết luận $0 Trên đây là toàn bộ lý thuyết gồm có khái niệm, tiến trình vẽ đồ thị hàm số bậc 2 lớp 10, đi kèm là bộ 20 thắc mắc trắc nghiệm VUIHOC có giải rõ ràng giúp những em học viên rèn luyện để thành thạo hơn dạng toán này. Để học nhiều hơn nữa về kiến thức và kỹ năng lớp 10, Toán THPT,... truy cập trang web trường học online vuihoc hoặc đăng ký ngay những khoá học cấp 3 môn Toán, Văn, Anh, Lý, Hoá, Sinh siêu có ích nhé!Review Bề lõm của parabol là gì ?
Bạn vừa đọc Post Với Một số hướng dẫn một cách rõ ràng hơn về Clip Bề lõm của parabol là gì tiên tiến nhất
Share Link Cập nhật Bề lõm của parabol là gì miễn phí
Bạn đang tìm một số trong những Chia Sẻ Link Cập nhật Bề lõm của parabol là gì Free.
Thảo Luận thắc mắc về Bề lõm của parabol là gì
Nếu sau khi đọc nội dung bài viết Bề lõm của parabol là gì vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Bề #lõm #của #parabol #là #gì - 2022-12-19 19:28:05
