Thủ Thuật về Giới hạn dãy số có chứa số mũ là n 2022
Dương Thế Tùng đang tìm kiếm từ khóa Giới hạn dãy số có chứa số mũ là n được Update vào lúc : 2022-12-05 08:04:10 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.Ta có: (lim left( n^3 - n^2 + n - 1 right) = lim n^3left( 1 - dfrac1n + dfrac1n^2 - dfrac1n^3 right) = + infty )
Nội dung chính Show- Giới hạn của hàm số, phương pháp tính và bài tập áp dụngGiới hạn hữu hạnBài tập áp dụng tìm giới hạnMối quan hệ giữa số lượng giới hạn một bên và số lượng giới hạn tại một điểmBảng những công thức tính số lượng giới hạn hàm sốMột số phương pháp tính lim thủ côngTính số lượng giới hạn của dãy sốCách tính lim bằng máy tínhChuyên đề số lượng giới hạn và liên tụcCÁCH TÍNH GIỚI HẠN HÀM SỐ NHƯ THẾ NÀO?
Dạng 1: Tính số lượng giới hạn dãy số hữu tỉ
Phương pháp:
- Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
- Bước 2: Tính những số lượng giới hạn của tử và mẫu rồi áp dụng quy tắc tính số lượng giới hạn của thương để tính số lượng giới hạn.
Ví dụ: Tính số lượng giới hạn (lim dfrac2n - 1n + 1).
Ta có: (lim dfrac2n - 1n + 1 = lim dfrac2 - dfrac1n1 + dfrac1n = dfrac21 = 2)
Dạng 2: Giới hạn của dãy số chứa căn thức
Phương pháp:
- Bước 1: Xét xem sử dụng phương pháp ở dạng 1 có dùng được không.
+) Nếu được thì ta dùng phương pháp ở dạng 1.
+) Nếu không ta sẽ chuyển qua bước dưới đây:
- Bước 2: Nhân, chia với biểu thức phối hợp thích hợp và đưa về dạng 1.
Ví dụ: Tính số lượng giới hạn (lim left( sqrt n^2 + 2n - n right)).
Ta có:
$lim left( sqrt n^2 + 2n - n right)=$ $ lim dfracleft( sqrt n^2 + 2n - n right)left( sqrt n^2 + 2n + n right)left( sqrt n^2 + 2n + n right) $ $= lim dfracn^2 + 2n - n^2left( sqrt n^2 + 2n + n right)$ $= lim dfrac2nsqrt n^2 + 2n + n$ $= lim dfrac2sqrt 1 + dfrac2n + 1 = dfrac21 + 1 = 1$
Dạng 3: Dãy số chứa lũy thừa, mũ.
Phương pháp:
- Bước 1: Chia cả tử và mẫu cho lũy thừa với cơ số lớn số 1.
- Bước 2: Sử dụng nhận xét (lim q^n = 1) với (left| q right| < 1).
Ví dụ: (lim dfrac2^n + 5^n2.3^n + 3.5^n = lim dfracleft( dfrac25 right)^n + 12.left( dfrac35 right)^n + 3.1 = dfrac0 + 12.0 + 3 = dfrac13)
Dạng 4: Tính số lượng giới hạn dẫn chứng tỏ hoặc dùng định nghĩa.
Phương pháp:
Sử dụng định lý kẹp: Cho ba dãy số (left( u_n right),left( v_n right),left( w_n right)).
Nếu (u_n < v_n < w_n,forall n) và (lim u_n = lim w_n = L Rightarrow lim v_n = L).
Ví dụ: Tính (lim dfracsin 3nn).
Ta có: ( - 1 le sin 3n le 1 Rightarrow dfrac - 1n le dfracsin 3nn le dfrac1n)
Mà (lim left( - dfrac1n right) = 0;lim left( dfrac1n right) = 0) nên (lim dfracsin 3nn = 0).

3.6/5 - (119 bầu chọn)
Mục Lục
- Giới hạn của hàm số, phương pháp tính và bài tập áp dụng
- Giới hạn hữu hạn
- Giới hạn vô cực, Giới hạn ở vô cựcGiới hạn 1 bên
- Chứng minh một dãy số có giới hạnTính số lượng giới hạn của hàm số
- TÍNH GIỚI HẠN HÀM SỐ DẠNG XÁC ĐỊNHTÌM GIỚI HẠN HÀM SỐ DẠNG BẤT ĐỊNH1. TÌM GIỚI HẠN CỦA HÀM SỐ DẠNG 0 TRÊN 0GIỚI HẠN DẠNG VÔ CÙNG TRÊN VÔ CÙNGGIỚI HẠN DẠNG VÔ CÙNG TRỪ VÔ CÙNGGIỚI HẠN DẠNG 1 MŨ VÔ CÙNGGIỚI HẠN DẠNG 0 NHÂN VÔ CÙNG
Giới hạn của hàm số, phương pháp tính và bài tập áp dụng
Giới hạn hữu hạn

 Giới hạn vô cực, Giới hạn ở vô cực
Giới hạn vô cực, Giới hạn ở vô cực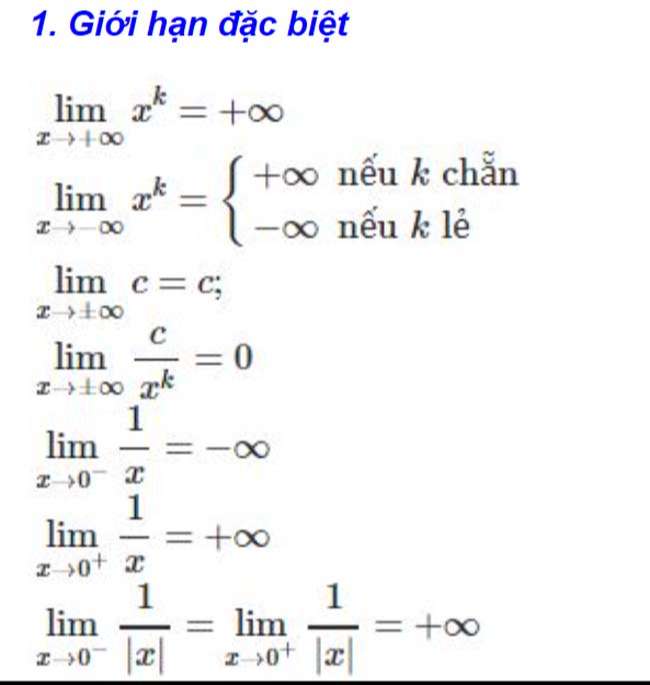

 Giới hạn 1 bên
Giới hạn 1 bên

Bài tập áp dụng tìm số lượng giới hạn











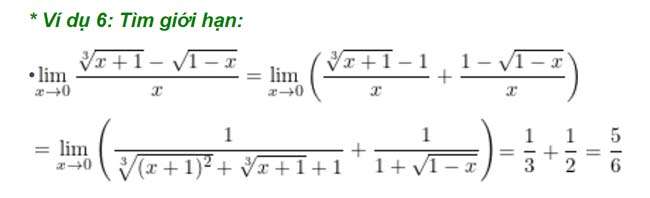






Ví dụ 8: Tìm số lượng giới hạn sau











Mối quan hệ giữa số lượng giới hạn một bên và số lượng giới hạn tại một điểm




Bảng những công thức tính số lượng giới hạn hàm số
Một số phương pháp tính lim thủ công
Tính số lượng giới hạn của dãy số
Cách 1: Sử dụng định nghĩa tìm số lượng giới hạn 0 của dãy số
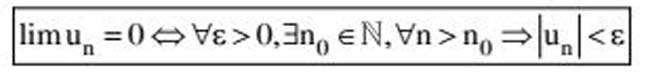
Cách 2: Tìm số lượng giới hạn của dãy số bằng công thức
Một số công thức ta thường gặp khi tính số lượng giới hạn hàm số như sau:

Công thức trên hoàn toàn có thể biến tấu thành những dạng khác tuy nhiên về bản chất thì không thay đổi.
Cách 3: Sử dụng định nghĩa tìm số lượng giới hạn hữu hạn
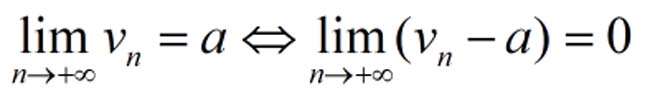
Cách 4: Sử dụng những số lượng giới hạn đặc biệt cùng với định lý để xử lý và xử lý những bài toán tìm số lượng giới hạn dãy số
- Ta thường sử dụng những dạng số lượng giới hạn:
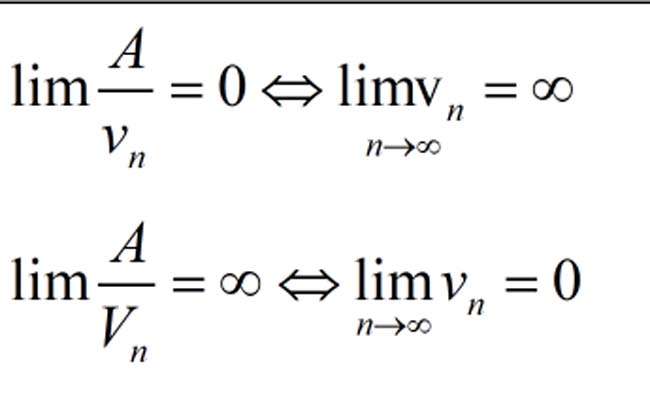
- Nếu biểu thức có dạng phân thức tử số và mẫu số chứa lũy thừa của n thì ta tiến hành chia cả tử và mẫu cho n^k với k là mũ cao nhất ở bậc mẫu.Nếu biểu thức chứa căn thức cần nhân một lượng phối hợp để đưa về dạng cơ bản thì ta có một số trong những lượng liên hợp thiết yếu như sau:
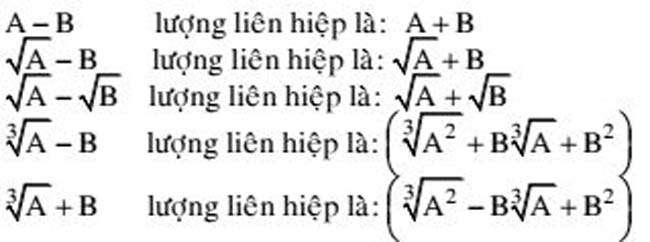
Cách 5: Áp dụng công thức tính tổng cấp số nhân lùi vô hạn, tính số lượng giới hạn, biểu thị một số trong những thập phân vô hạn tuần hoàn thành xong phân số.
- Cấp số nhân lùi vô hạn là cấp số nhân vô hạn và có công bội là |q| < 1Tổng những số hạng của một cấp số nhân lùi vô hạn (Un)
S = u1 + u2 + u3 + u4 + …. + un = u1 / ( 1 – q )
- Mọi số thập phân đều được biểu thị dưới dạng lũy thừa của 10.
Câu 6: Tìm số lượng giới hạn vô cùng của một dãy số bằng định nghĩa
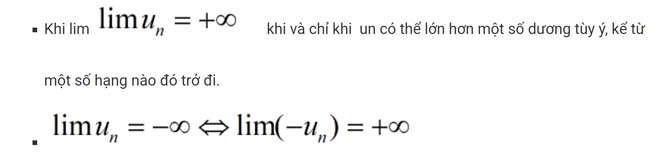
Cách 7: Tìm số lượng giới hạn của một dày số bằng phương pháp sử dụng định lý, quy tắc tìm số lượng giới hạn vô cực
Chứng minh một dãy số có số lượng giới hạnÁp dụng định lý Vâyơstraxơ:
- Nếu dãy số (un) tăng và bị chặn trên thì nó có số lượng giới hạn.Nếu dãy số (un) giảm và bị chặn dưới thì nó có số lượng giới hạn.
Chứng minh tính tăng và tính bị chặn:
Chứng minh một dãy số tăng và bị chặn trên (dãy số tăng và bị chặn dưới) bởi số M ta thực hiện: Tính một vài số hạng đầu tiên của dãy và quan sát mối liên hệ để Dự kiến chiều tăng (chiều giảm) và số M.
Tính số lượng giới hạn của dãy số ta thực hiện theo một trong hai phương pháp sau:
Phương pháp 1
Đặt lim un = a. Từ lim u(n+1) = lim f(un) ta được một phương trình theo ẩn a.
Giải phương trình tìm nghiệm a và số lượng giới hạn của dãy (un) là một trong những nghiệm của phương rình. Nếu phương trình có nghiệm duy nhất thì đó đó đó là số lượng giới hạn cảu dãy cần tìm. còn nếu phương trình có nhiều hơn nữa một nghiệm thì nhờ vào tính chất của dãy số để loại nghiệm.
Chú ý: Giới hạn của dãy số nếu có là duy nhất.
Phương pháp 2: Tìm công thức tổng quát un của dãy số bằng phương pháp Dự kiến. Chứng minh công thức tổng quát un bằng phương pháp quy nạp toán học. Tính số lượng giới hạn của dãy thông qua công thức tổng quát đó.
Tính số lượng giới hạn của hàm sốĐể tính số lượng giới hạn của hàm số ta hoàn toàn có thể thực hiện một số trong những phương pháp như sau:
- Dùng định nghĩa để tìm giới hạnTìm số lượng giới hạn của hàm số bằng công thứcSử dụng định nghĩa tìm số lượng giới hạn một bênSử dụng định lí và công thức tìm giới hạn một bênTính số lượng giới hạn vô cựcTìm số lượng giới hạn của hàm số dạng 0/0Dạng vô định
Dưới đây là một số trong những công thức tính hàm số vô cùng cơ bản:

Cách tính lim bằng máy tính
Bước 1: Trước tiên hãy nhập biểu thức vào máy tính
Bước 2: Sử dụng hiệu suất cao đó là gán số tính giá trị biểu thức
Bước 3: Lưu ý gán những giá trị theo phía dưới:
+) Lim về vô cùng dương thì hãy gán số 100000
+) Lim về vô cùng âm thì hãy gán số -100000
+) Lim về 0 thì hãy gán số 0.00000001
+) Lim về số bất kì ví dụ như về +3 thì gán 3.000000001 còn về 3- thì gán 2.9999999999
Tính lim là một dạng bài tập khá cơ bản, tuy nhiên dạng toán này vẫn chiếm một vài câu trong đề thi trung học phổ thông quốc gia. Các bạn cần đảm bảo tính đúng chuẩn khi làm. Đặc biệt hoàn toàn có thể sử dụng máy tính Casio để hoàn toàn có thể tính toán nhanh và đúng chuẩn nhất.
Chuyên đề số lượng giới hạn và liên tục
CÁCH TÍNH GIỚI HẠN HÀM SỐ NHƯ THẾ NÀO?
TÍNH GIỚI HẠN HÀM SỐ DẠNG XÁC ĐỊNHNếu hàm f(x) xác định tại điểm lấy số lượng giới hạn. Thì ta chỉ việc thay điểm đó vào biểu thức dưới dấu lim sẽ được kết quả cần tìm.
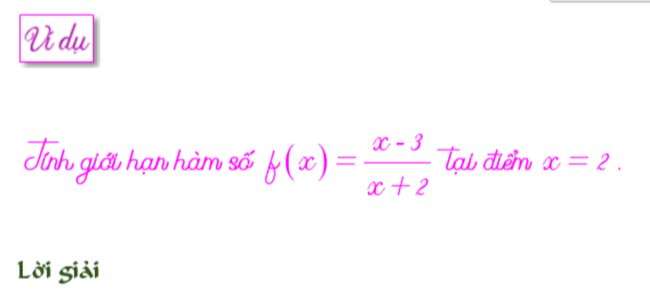
Ta chỉ việc thay x=2 vào biểu thức trong dấu lim ta được -1/4. Và đó đó đó là kết quả của số lượng giới hạn trên.
TÌM GIỚI HẠN HÀM SỐ DẠNG BẤT ĐỊNHĐối với dạng bất định ta quan tâm tới một số trong những dạng thường gặp như sau:
1. TÌM GIỚI HẠN CỦA HÀM SỐ DẠNG 0 TRÊN 0Đối với dạng 0 trên 0 ta lại phân thành 2 loại: Loại số lượng giới hạn không chứa căn và loại chứa căn.
Loại không chứa căn gồm có nhiều chủng loại số lượng giới hạn đặc biệt và loại phân thức mà tử và mẫu là những đa thức.
Giới hạn đặc biệt dạng 0 trên 0 được đề cập đến trong chương trình phổ thông lúc bấy giờ là:

Cách tính số lượng giới hạn dạng 0 trên 0 loại đa thức trên đa thức thì ta phân tích thành nhân tử bằng lược đồ Hoocner.
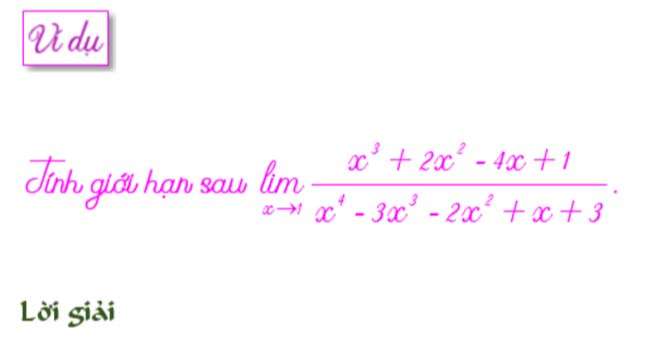
Ta thấy x=1 là nghiệm của tất cả tử số và mẫu số. Ta dùng lược đồ Hoocner để phân tích tử số và mẫu số.

Còn để tính loại chứa căn ta thực hiện nhân cả tử và mẫu với biểu thức phối hợp.
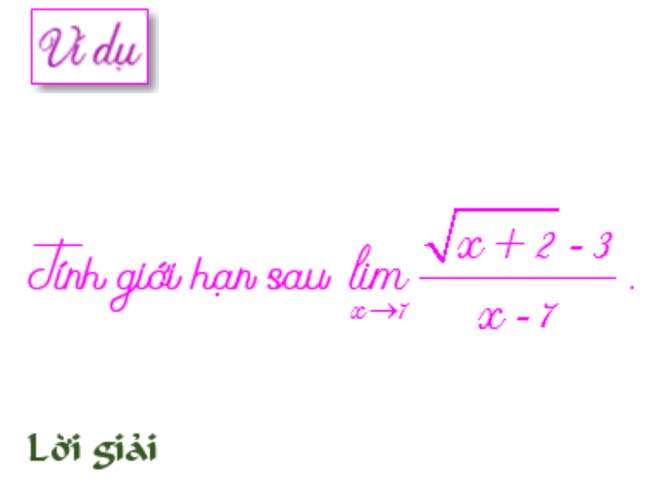

Với căn bậc 3 ta cũng làm tương tự.

Ta có:

Trong trường hợp số lượng giới hạn có cả căn bậc 2 và căn bậc 3 thì ta thêm bớt 1 lượng để đưa về tổng hiệu của 2 số lượng giới hạn dạng 0 trên 0.

 GIỚI HẠN DẠNG VÔ CÙNG TRÊN VÔ CÙNG
GIỚI HẠN DẠNG VÔ CÙNG TRÊN VÔ CÙNGVới dạng số lượng giới hạn vô cùng trên vô cùng ta giải bằng phương pháp chia cả tử và mẫu cho x với số mũ cao nhất của tử hoặc của mẫu. Lưu ý dạng này khi x tiến tới âm vô cùng tất cả chúng ta hay nhầm lẫn về dấu. Cụ thể khi đưa x vào trong căn bậc 2 ta cần để dấu – bên phía ngoài.

 GIỚI HẠN DẠNG VÔ CÙNG TRỪ VÔ CÙNG
GIỚI HẠN DẠNG VÔ CÙNG TRỪ VÔ CÙNGVới dạng vô cùng trừ vô cùng (vô cực trừ vô cực) ta thực hiện theo 2 phương pháp: Nhóm ẩn bậc cao nhất hoặc nhân phối hợp. Cách nào thuận lợi hơn ta tiến hành theo cách đó.
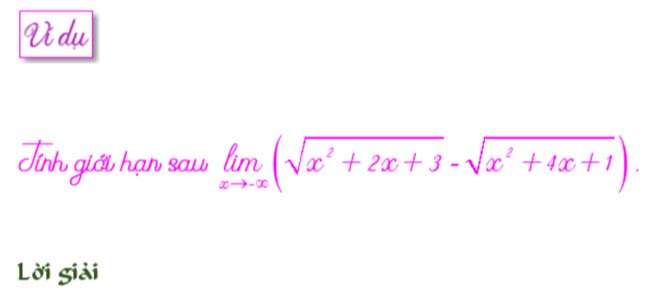
Trường hợp này tất cả chúng ta cần nhân phối hợp chính bới nếu nhóm x thì sẽ lại đưa về dạng bất định 0 nhân vô cùng.


Bài này giống bài trên đều là dạng vô cùng trừ vô cùng. Nhưng ta lại để ý là thông số bậc cao nhất trong 2 căn là rất khác nhau. Vì vậy bài này tất cả chúng ta nên nhóm nhân tử chung.
 GIỚI HẠN DẠNG 1 MŨ VÔ CÙNG
GIỚI HẠN DẠNG 1 MŨ VÔ CÙNGVới số lượng giới hạn dạng 1 mũ vô cùng ta tính thông qua số lượng giới hạn đặc biệt sau:
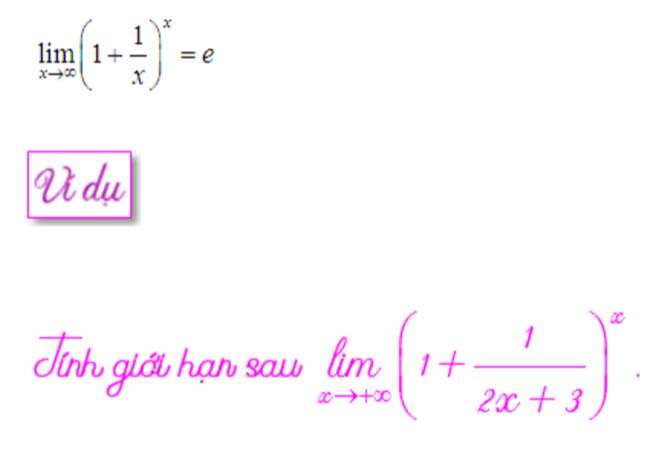
 GIỚI HẠN DẠNG 0 NHÂN VÔ CÙNG
GIỚI HẠN DẠNG 0 NHÂN VÔ CÙNGVề bản chất số lượng giới hạn dạng 0 nhân vô cùng hoàn toàn có thể đưa về dạng 0 trên 0 hoặc dạng vô cùng trên vô cùng qua 1 vài phép biến hóa theo lưu ý ở đầu nội dung bài viết này phần định nghĩa. Với dạng số lượng giới hạn này tất cả chúng ta nên biến hóa về dạng xác định hoặc những dạng số lượng giới hạn vô định đã nêu ra ở trên. Tùy từng bài rõ ràng tất cả chúng ta cần biến hóa cho phù hợp.
Tải thêm tài liệu liên quan đến nội dung bài viết Giới hạn dãy số có chứa số mũ là n