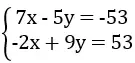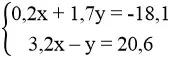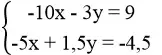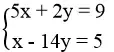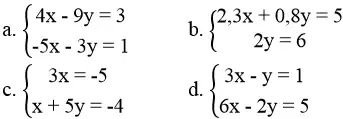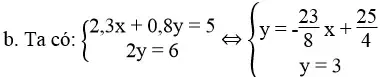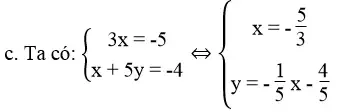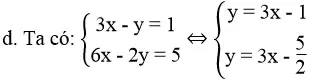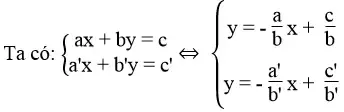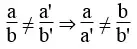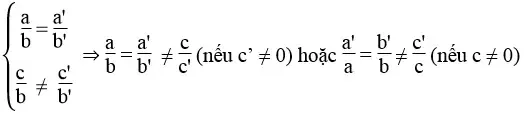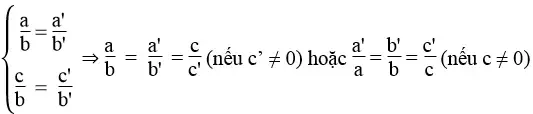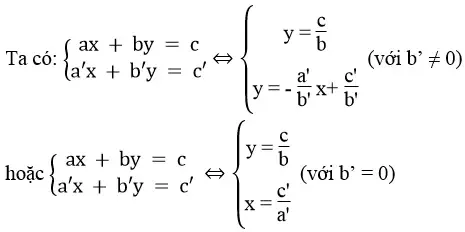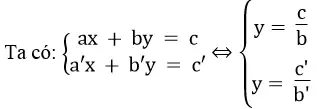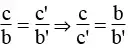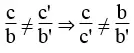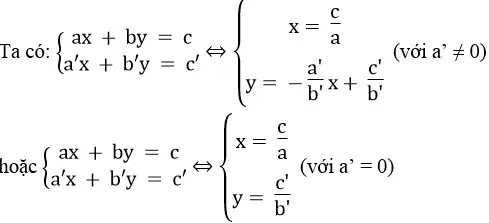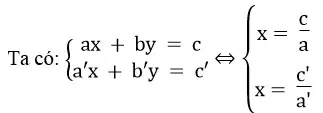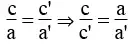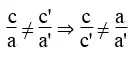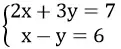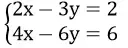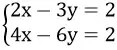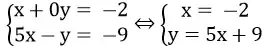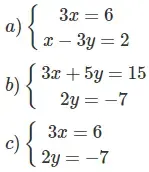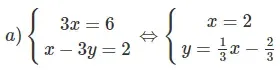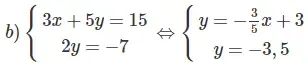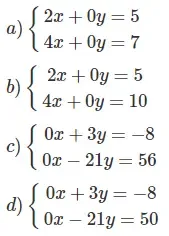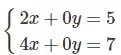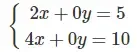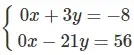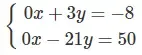Thủ Thuật Hướng dẫn Biểu thức nào sau đây kiểm tra phương trình số 1 có vô số nghiệm 2022
Họ và tên học viên đang tìm kiếm từ khóa Biểu thức nào sau đây kiểm tra phương trình số 1 có vô số nghiệm được Update vào lúc : 2022-03-27 13:17:07 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Sách Giải Sách Bài Tập Toán 9 Bài 2: Hệ hai phương trình số 1 hai ẩn giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 9 sẽ giúp bạn rèn luyện kĩ năng suy luận hợp lý và hợp logic, hình thành kĩ năng vận dụng kết thức toán học vào đời sống và vào những môn học khác:
a. (-4; 5)
b. (3; -11)
c. (1,5; 2), (3; 7)
d. (1; 8)
Lời giải:
a. Thay x = -4, y = 5 vào từng phương trình của hệ:
7.(-4) – 5.5 = -28 – 25 = -53
-2.(-4) + 9.5 = 8 + 45 = 53
Vậy (-4; 5) là nghiệm của hệ phương trình 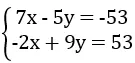
b. Thay x = 3, y = -11 vào từng phương trình của hệ:
0,2.3 + 1,7.(-11) = 0,6 – 18,7 = -18,1
3,2.3 – 1.(-11) = 9,6 + 11 = 20,6
Vậy (3; -11) là nghiệm của hệ phương trình 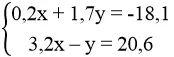
c. * Thay x = 1,5, y = 2 vào từng phương trình của hệ:
10.1,5 – 3.2 = 15 – 6 = 9
-5.1,5 + 1,5.2 = -7,5 + 3 = -4,5
Vậy (1,5; 2) là nghiệm của hệ phương trình 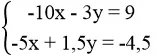
* Thay x = 3, y = 7 vào từng phương trình của hệ:
10.3 – 3.7 = 30 – 21 = 9
-5.3 + 1,5.7 = -15 + 10,5 = -4,5
Vậy (3; 7) là nghiệm của hệ phương trình 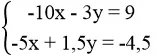
d. Thay x = 1, y = 8 vào từng phương trình của hệ:
5.1 + 2.8 = 5 + 16 = 21 ≠ 9
Vậy (1; 8) không là nghiệm của hệ phương trình 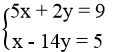
Lời giải:
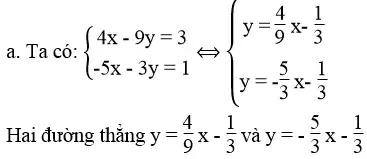
Vậy hệ phương trình có một nghiệm duy nhất.
Vì đường thẳng y = 3 song song với trục hoành còn đường thẳng 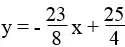
Vậy hệ phương trình có một nghiệm duy nhất.
Vì đường thẳng x = – 5/3 song song với trục tung còn đường thẳng 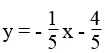 cắt hai trục tọa độ nên chúng cắt nhau.Vậy hệ phương trình có một nghiệm duy nhất.
cắt hai trục tọa độ nên chúng cắt nhau.Vậy hệ phương trình có một nghiệm duy nhất.
Vì hai tuyến đường thẳng có thông số góc đều bằng 3 nhưng tung độ gốc rất khác nhau (-1 ≠ – 5/2 ) nên chúng song song với nhau.
Vậy hệ phương trình vô nghiệm.
a. Hãy cho thêm một phương trình số 1 hai ẩn để được một hệ có nghiệm duy nhất.
b. Hãy cho thêm một phương trình số 1 hai ẩn để được một hệ vô nghiệm.
c. Hãy cho thêm một phương trình số 1 hai ẩn để được một hệ có vô số nghiệm.
Lời giải:
Ta có: 3x – 2y = 5 ⇔ 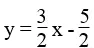
a. Để được một hệ có nghiệm duy nhất thì cần thêm một phương trình số 1 hai ẩn có thông số góc khác 3/2 .
Chẳng hạn: 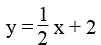 ⇔ -x + 2y = 4
⇔ -x + 2y = 4
Khi đó ta có hệ 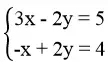
b. Để được một hệ vô nghiệm thì cần thêm một phương trình số 1 hai ẩn có thông số góc bằng 3/2 và tung độ gốc khác – 5/2 .
Chẳng hạn: 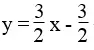 ⇔ 3x – 2y = 3
⇔ 3x – 2y = 3
Khi đó ta có hệ 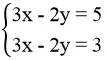
c. Để được một hệ có vô số nghiệm thì cần thêm một phương trình số 1 hai ẩn có thông số góc bằng 3/2 và tung độ gốc bằng – 5/2 .
Chẳng hạn: 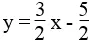 ⇔ 6x – 4y = 10
⇔ 6x – 4y = 10
Khi đó ta có hệ 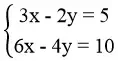
a. Có nghiệm duy nhất
b. Vô nghiệm
c. Có vô số nghiệm
Áp dụng:
a. Lập một hệ hai phương trình số 1 hai ẩn có nghiệm duy nhất.
b. Lập một hệ hai phương trình số 1 hai ẩn vô nghiệm.
c. Lập một hệ hai phương trình số 1 hai ẩn có vô số nghiệm.
Lời giải:
Xét những trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
a. Hệ phương trình có một nghiệm duy nhất lúc hai tuyến đường thẳng cắt nhau. Nghĩa là hai tuyến đường thẳng có thông số góc rất khác nhau:
b. Hệ phương trình vô nghiệm khi hai tuyến đường thẳng song song nhau. Nghĩa là hai tuyến đường thẳng có thông số góc bằng nhau và tung độ gốc rất khác nhau:
c. Hệ phương trình có vô số nghiệm khi hai tuyến đường thẳng trùng nhau. Nghĩa là hai tuyến đường thẳng có thông số góc và tung độ gốc bằng nhau:
*a = 0, a’ ≠ 0
Vì hai tuyến đường thẳng 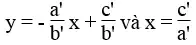
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
Hệ có vô số nghiệm khi hai tuyến đường thẳng trùng nhau, nghĩa là:
Hệ vô nghiệm khi hai tuyến đường thẳng song song nhau, nghĩa là:
*b = 0, b’ ≠ 0
Vì hai tuyến đường thẳng 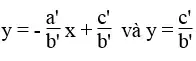
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
Hệ có vô số nghiệm khi hai tuyến đường thẳng trùng nhau, nghĩa là:
Hệ vô nghiệm khi hai tuyến đường thẳng song song nhau, nghĩa là:
Áp dụng:
a. Hệ hai phương trình số 1 hai ẩn có nghiệm duy nhất:
b. Hệ hai phương trình số 1 hai ẩn vô nghiệm:
c. Hệ hai phương trình số 1 hai ẩn có vô số nghiệm:
Lời giải:
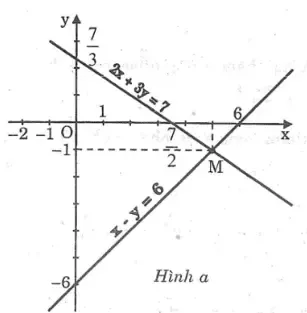
a. *Ta có: 2x + 3y = 7 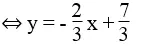
Cho x = 0 thì y = 7/3 ⇒ (0; 7/3 )
Cho y = 0 thì x = 7/2 ⇒ (7/2 ; 0)
*Ta có: x – y = 6 ⇔ y = x – 6
Cho x = 0 thì y = -6 ⇒ (0; -6)
Cho y = 0 thì x = 6 ⇒ (6; 0)
Hai đường thẳng cắt nhau tại M(5; -1) nên nghiệm của hệ phương trình là (x; y) = (5; -1)
Đồ thị: hình a.
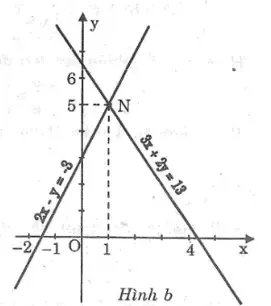
b. *Ta có: 3x + 2y = 13 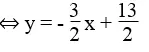
Cho x = 0 thì y = 13/2 ⇒ (0; 13/2 )
Cho y = 0 thì x = 13/3 ⇒ (13/3 ; 0)
*Ta có: 2x – y = -3 ⇔ y = 2x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = – 3/2 ⇒ (- 3/2 ; 0)
Hai đường thẳng cắt nhau tại N(1; 5) nên nghiệm của hệ phương trình là (x; y) = (1; 5).
Đồ thị: hình b.
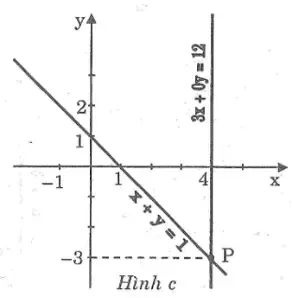
c. *Ta có: x + y = 1 ⇔ y = -x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1 ⇒ (1; 0)
*Ta có: 3x + 0y = 12 ⇔ x = 4
Hai đường thẳng cắt nhau tại P(4; -3) nên nghiệm của hệ phương trình là (x; y) = (4; -3)
Đồ thị: hình c.
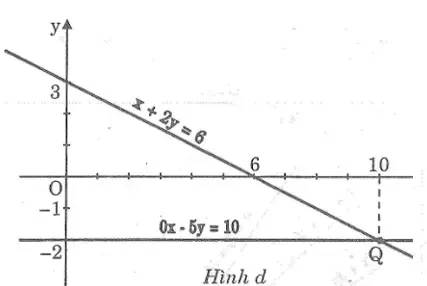
d. *Ta có: x + 2y = 6 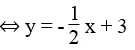
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = 6 ⇒ (6; 0)
*Ta có: 0x – 5y = 10 ⇔ y = -2
Hai đường thẳng cắt nhau tại Q.(10; -2) nên nghiệm của hệ phương trình là (x; y) = (10; -2)
Đồ thị: hình d.
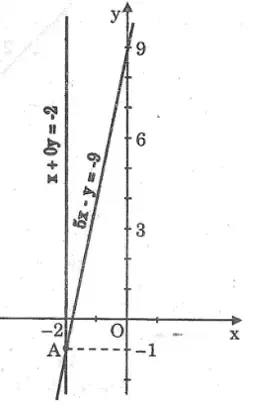
a. Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ.
b. Nghiệm của hệ phương trình này liệu có phải là nghiệm của phương trình 3x – 7y = 1 hay là không?
Lời giải:
a. Ta có:
*Vẽ đường thẳng x = -2 song song với trục tung
*Vẽ đường thẳng y = 5x + 9
Cho x = 0 thì y = 9 ⇒ (0; 9)
Cho y = 0 thì x = – 9/5 = -1,8
Hai đường thẳng y = 5x + 9 và x = -2 cắt nhau tại A(-2; -1). Vậy hệ phương trình có một nghiệm duy nhất (x; y) = (-2; -1).
b. Thay x = -2, y = -1 vào phương trình 3x – 7y = 1, ta có:
3.(-2) – 7.(-1) = -6 + 7 = 1
Vậy x và y thỏa phương trình 3x – 7y = 1 nên (x; y) = (-2; -1) là nghiệm của phương trình 3x – 7y = 1.
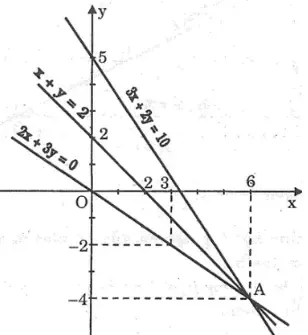
Hỏi đường thẳng (d3): 3x + 2y = 10 có đi qua giao điểm của (d1) và (d2) hay là không?
Lời giải:
Vẽ đường thẳng (d1) là đồ thị hàm số y = -x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2 ⇒ (2; 0)
Vẽ đường thẳng (d2) là đồ thị hàm số 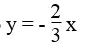
Cho x = 0 thì y = 0 ⇒ (0; 0)
Cho x = 3 thì y = -2 ⇒ (3; -2)
Hai đường thẳng (d1) và (d2) cắt nhau tại A(6; -4). Thay những giá trị x và y này vào phương trình đường thẳng (d3), ta có:
3.6 + 2.(-4) = 18 – 8 = 10.
Vậy x và y thỏa phương trình 3x + 2y = 10 nên (x; y) = (6; -4) là nghiệm của phương trình 3x + 2y = 10.
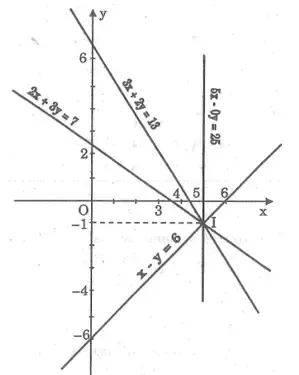
Lời giải:
Ta có: (d3): x – y = 6 ⇔ y = x – 6
(d4): 5x – 0y = 25 ⇔ x = 5
Vẽ đường thẳng (d3) là đồ thị hàm số y = x – 6
Cho x = 0 thì y = -6 ⇒ (0; -6)
Cho y = 0 thì x = 6 ⇒ (6; 0)
Vẽ đường thẳng (d4) là đường thẳng x = 5
Hai đường thẳng (d3) và (d4) cắt nhau tại I(5; -1). Lần lượt thay những giá trị x và y này vào phương trình đường thẳng (d1) và (d2), ta có:
(d1): 3.5 + 2.(-1) = 15 – 2 = 13
(d2): 2.5 + 3.(-1) = 10 – 3 = 7.
Vậy x và y thỏa mãn hai phương trình 3x + 2y = 13 và 2x + 3y = 7 nên (x; y) = (5; -1) là nghiệm của những phương trình trên. Hay là (d1) và (d2) đều đi qua I(5; -1).
Vậy bốn đường thẳng (d1): 3x + 2y = 13, (d2): 2x + 3y = 7, (d3): x – y = 6, (d4): 5x – 0y = 25 đồng quy.
Lời giải:
Ta có đường thẳng x = 2 song song với trục tung. Đường thẳng 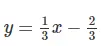 cắt trục tung nên hai tuyến đường thẳng đó cắt nhau. Hệ phương trình có một nghiệm duy nhất.
cắt trục tung nên hai tuyến đường thẳng đó cắt nhau. Hệ phương trình có một nghiệm duy nhất.
Ta có đường thẳng y = -3,5 song song với trục hoành
Đường thẳng 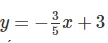 cắt trục hoành nên hai tuyến đường thẳng đó cắt nhau. Hệ phương trình có một nghiệm duy nhất
cắt trục hoành nên hai tuyến đường thẳng đó cắt nhau. Hệ phương trình có một nghiệm duy nhất
Đường thẳng 3x = 6 song song với trục tung. Đường thẳng 2y = -7 cắt trục tung nên hai tuyến đường thẳng đó cắt nhau. Hệ phương trình có một nghiệm duy nhất
Lời giải:
a) Đường thẳng 2x + 0y = 5 ⇔ x = 2,5 song song với trục tung
Đường thẳng 4x + 0 y = 7 ⇔ x = 1,75 song song với trục tung nên chúng cũng song song với nhau.
Vậy hệ
vô nghiệm
b) Đường thẳng 2x + 0y = 5 và đường thẳng 4x + 0y = 10 trùng nhau
Vậy hệ
vô nghiệm
c) Đường thẳng 0x + 3y = -8 ⇔ x = -8/3 và đường thẳng 0x – 21y = 56 ⇔ y = -8/3 trùng nhau. Vậy hệ
có vô số nghiệm
d) Đường thẳng 0x + 3y = -8 là đường thẳng y = -8/3 song song với trục hoành nên chúng song song với nhau. Hệ
vô nghiệm.
[embed]https://www.youtube.com/watch?v=vBjss37U_2A[/embed]