Thủ Thuật về Hình bình hành có hai cặp cạnh đối song song đúng hay sai Chi Tiết
Lê Minh Long đang tìm kiếm từ khóa Hình bình hành có hai cặp cạnh đối song song đúng hay sai được Cập Nhật vào lúc : 2022-04-05 05:37:10 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha.HÌNH BÌNH HÀNH KIẾN THỨC CẨN NHỚ GIỚI THIỆU HÌNH BÌNH HÀNH Hình bình hành là hình tứ giác có hai cặp cạnh đối diện song song và bằng nhau. Hình bình hành ABCD có: D c Hình bình hành ABCD Ví dụ: AB và DC là hai cạnh đối diện; AD và BC là hai cạnh đối diện. Cạnh AB song song với cạnh DC. Cạnh AD song song với cạnh BC. AB = DC và AD = BC. DIỆN TÍCH HÌNH BÌNH HÀNH Diện tích hình bình hành bằng độ dài đáy nhân với độ cao (cùng một dơn vị đo). s = a X h (S là diện tích s quy hoạnh, a là độ dài đáy, h là độ cao của hình bình hành). B • DC là đáy của hình bình hành. AH vuông góc vái DC. Độ dài AH là độ cao của hình bình hành. Độ dài đáy HƯỚNG DẪN GIẢI BÀI TẬP ❖ Bài 1 Trong những hình sau, hình nào là hình bình hành? Hình 4 Hình 1. hình 2 và hình 5 là hình bình hành. cặp cạnh đối diện song song và Giải ❖ Bài 2 Cho biết trong hình tứ giác ABCD: AB và DC là hai cạnh đối diện. AD và BC là hai cạnh đô'i diện. Hình tứ giác ABCD và hình bình hành MNPQ, trong hai hình đó, hình nào có cặp cạnh đối diện song song và bằng nhau? Giải MNPQ là hình bình hành nên có những bằng nhau.
Nội dung chính- Các tín hiệu nhận ra hình bình hànhCách chứng tỏ hình bình hànhBài tập về chứng tỏ hình bình hànhVideo liên quan
Hình bình hành là tứ giác có những cạnh dối song song. Lý thuyết hình bình hành – Hình bình hành
1. Định nghĩa:
Hình bình hành là tứ giác có những cạnh dối song song.
ABCD là hình bình hành ⇔ 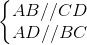
Nhận xét: HÌnh bình hành là một hình thang có hai cạnh bên song song.
2. Tính chất:
Định lí: Trong hình bình hành:
a) Các cạnh đối bằng nhau.
b) Các góc đối bằng nhau.
Quảng cáoc) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận ra
a) Tứ giác có những cạnh đối song song là hình bình hành.
b) Tứ giác có những cạnh đối bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
d) Tứ giác có những góc đối bằng nhau là hình bình hành.
e) Tứ giác có hai tuyến đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Hình bình hành là tứ giác có 2 cặp cánh đối song song với nhau. Đây là một dạng đặc biệt của hình thang. Bài viết này, Boxthuthuat sẽ chia sẻ với những bạn về tín hiệu nhận ra hình bình hành, cách chứng tỏ một tứ giác là hình bình hành.
Các tín hiệu nhận ra hình bình hành
Nếu một tứ giác có những tín hiệu dưới đây thì tứ giác đó là một hình bình hành:
Có hai cặp cạnh đối song song Có những cạnh đối bằng nhau Có một cặp cạnh đối vừa song song và vừa bằng nhau Có góc đối bằng nhau Có hai tuyến đường chéo cắt nhau tại trung điểm của mỗi đườngNếu một hình thang có những tín hiệu dưới đây thì tứ giác đó là một hình bình hành:
6. Có hai cạnh đáy bằng nhau
7. Có hai cạnh bên song song với nhau
Hình thoi, hình chữ nhật, hình vuông vắn là những dạng đặc biệt của hình bình hành.
Cách chứng tỏ hình bình hành
Để chứng tỏ một tứ giác là hình bình hành, tất cả chúng ta sẽ nhờ vào những tín hiệu nhận ra hình bình hành như đã nếu ở trên, hoặc chứng tỏ tứ giác đó là hình thang sau đó nhờ vào những tín hiệu nhận ra hình bình hành qua hình thang để chứng tỏ tiếp.Công thức tính chu vi, diện tích s quy hoạnh hình bình hành
Có thể bạn quan tâm: Công thức tính chu vi, diện tích s quy hoạnh hình bình hành
Bài tập về chứng tỏ hình bình hành
Bài 1: Các câu sau đúng hay sai?
a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành
b) Hình thang có hai cạnh bên song song là hình bình hành
c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành
d) Hình thang có hai cạnh bên bằng nhau là hình bình hành
Lời giải:
a) Đúng, vì hình thang có hai đáy song song lại sở hữu thêm hai cạnh đáy bằng nhau nên là hình bình hành theo tín hiệu nhận ra 5
b) Đúng, vì khi đó ta được tứ giác có những cạnh đối song song là hình bình hành (định nghĩa)
c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.
Bài 2. Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông như hình phía dưới có là hình bình hành hay là không?
Lời giải:
Cả ba tứ giác trên đề là hình bình hành vì:
– Tứ giác ABCD có AB // CD và AB=CD=3 ⇒ tứ giác này là hình bình hành (tín hiệu nhận ra 3)
– Tứ giác EFGH có EH // FG và EH=FH =3 ⇒ tứ giác này là hình bình hành (tín hiệu nhận ra 3)
– Tứ giác MNPQ có MN=PQ và MQ=NP ⇒ tứ giác này là hình bình hành (tín hiệu nhận ra 2)
(Chú ý:
– Hai tứ giác ABCD, EFGH còn tồn tại thể nhận ra là hình bình hành bằng tín hiệu nhận ra 2 (AB=CD, BC=AD; EF=GH, FG=EH)
– Tứ giác MNPQ còn tồn tại thể nhận ra là hình bình hành bằng tín hiệu nhận ra 5
Bài 3: Cho hình bình hành ABCD. Gọi E, F là trung điểm của AD, BC. Chứng minh rằng BE = DF
Lời giải:
Ta có:
DE = 1/2.AD; BF = 1/2.BC
ABCD là hình bình hành ⇒ AD = BF
=> DE = BF
Tứ giác BEDF có:
DE // BF (vì AD // BC)
DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF
Bài 4: Cho hình bình hành ABCD (AB>BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF
b) Tứ giác DEBF là hình gì? Vì sao?
Lời giải:
b) Tứ giác DEBF có:
DE // BF (chứng tỏ ở câu a)
BE // DF (vì AB // CD)
⇒ Tứ giác DEBF là hình bình hành.
Bài 5: Cho hình phía dưới. Trong số đó ABCD là hình bình hành, AH, CH cùng vuông góc với BD
a) Chứng minh rằng AHCK là hình bình hành
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
Lời giải:
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
∠D1 = ∠B1 (so le trong)
⇒ ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
⇒ AH = CK
Tứ giác AHCK có AH // CK, AH = CK ⇒ AHCK là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành. Do đó ba điểm A, O, C thẳng hàng.
Bài 6: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của những cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
Lời giải:
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (giả thiết)
Nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
⇒ EF // HG (1)
Chứng minh tương tự ⇒ EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận ra 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = 1/2.AC.
HG là đường trung bình của ∆ACD nên HG = 1/2 AC.
Suy ra EF = HG
Lại có EF // HG ( chứng tỏ trên)
Vậy EFGH là hình-bình-hành (tín hiệu nhận ra 3).
Bài 7: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Lời giải:
a) Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.
Tứ giác AICK có AK // IC, AK = IC nên là hình bình hành.
Do đó AI // CK
b) ∆DCN có DI = IC, IM // CN.
(vì AI // CK) nên suy ra DM = MN
Chứng minh tương tự đối với ∆ABM ta có MN = NB.
Vậy DM = MN = NB
Trên đây là chia sẻ về những tín hiệu nhận ra hình bình hành kèm hướng dẫn cách chứng tỏ tứ giác là hình bình hành, có ví dụ minh họa. Nếu có bất kỳ thắc mắc gì về phần kiến thức và kỹ năng này, hãy comment phía dưới nội dung bài viết nhé!
ID nội dung bài viết: 141656
[embed]https://www.youtube.com/watch?v=dBNhJH_U-uQ[/embed]
