Thủ Thuật về Tính thể tích khối chóp đáy là hình thang vuông Mới Nhất
Lê My đang tìm kiếm từ khóa Tính thể tích khối chóp đáy là hình thang vuông được Cập Nhật vào lúc : 2022-04-30 15:43:05 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và [B,AB=BC=2,AD=3] Cạnh bên [SA=2] và vuông góc với đáy. Tính thể tích khối chóp S.ABCD.
Nội dung chính- Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, , và khoảng chừng cách từ điểm A đếnmp(SCD) bằng a. Tính thể tích của khối chóp S.ABCD.
Bài tập trắc nghiệm 60 phút Thể tích khối chóp - Khối đa diện và thể tích - Toán Học 12 - Đề số 34Video liên quan
[V=frac10sqrt33]
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, , và khoảng chừng cách từ điểm A đếnmp(SCD) bằng a. Tính thể tích của khối chóp S.ABCD.
A.
.
B.
.
C.
.
D.
.
Đáp án và lời giải
Đáp án:D
Lời giải:
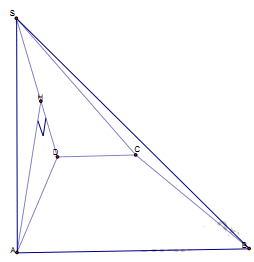
Kẻ AH vuông góc với SD.
.
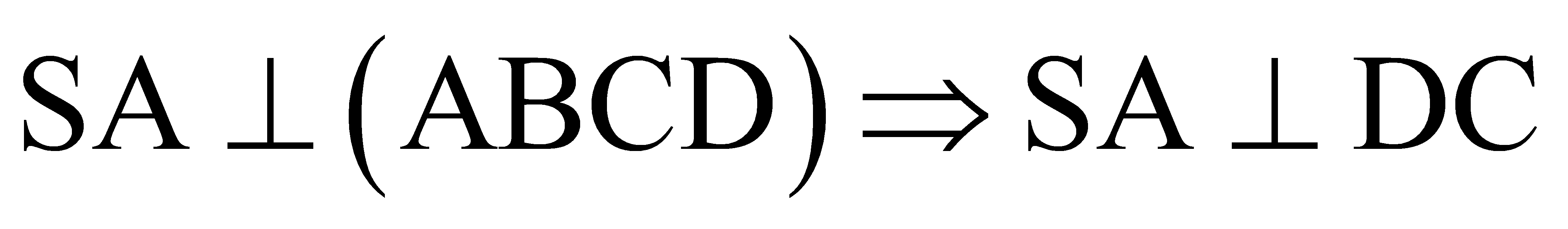
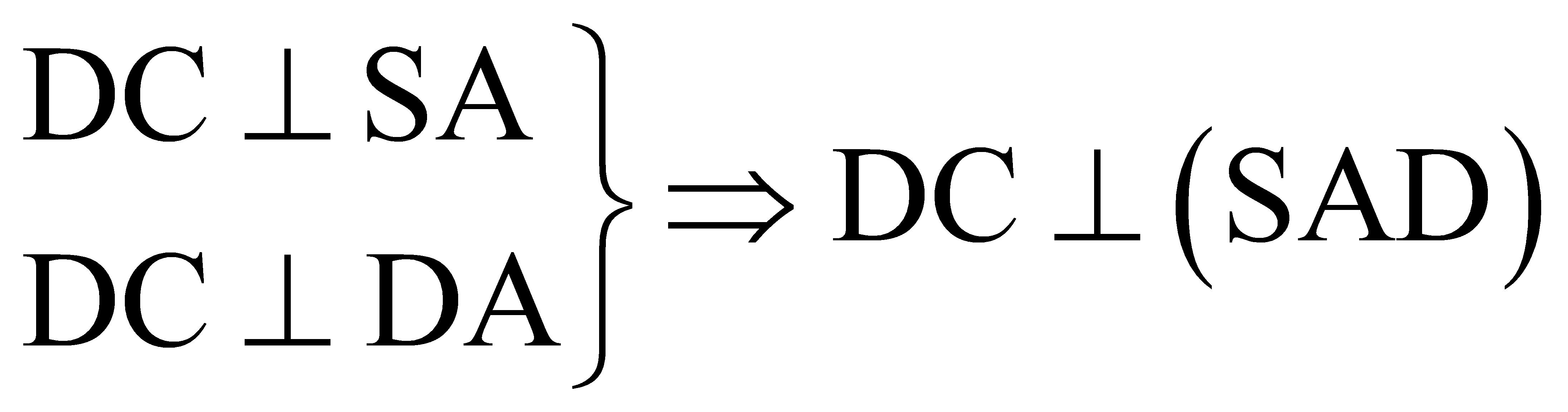
Vậy đáp án đúng là: D.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 60 phút Thể tích khối chóp - Khối đa diện và thể tích - Toán Học 12 - Đề số 34
Làm bài
Chia sẻ
Một số thắc mắc khác cùng bài thi.
Cho hình chóp S.ABCD xuất hiện phẳng (SAB) vuông góc với mặt phẳng (ABCD), đáy ABCD là hình vuông vắn,
. Gọi M là trung điểm của CD. Thể tích của khối chóp S.ABCM là:
Cho hình chóp S.ABCD có đáy là hình bình hành với
; góc 
. SA vuông góc với đáy; góc giữa SC và mặt phẳng đáy là 60 độ. Thể tính khối chóp S.ABCD là V. Tỉ số 
là:
Cho hìnhchóptứgiácđềuS.ABCD cócạnhđáybằng2a, gócgiữamặtbênvàmặtđáybằng
GọiM, N lầnlượtlàtrungđiểmcủacáccạnhSD, DC. ThểtíchkhốitứdiệnACMN là
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D,
, 
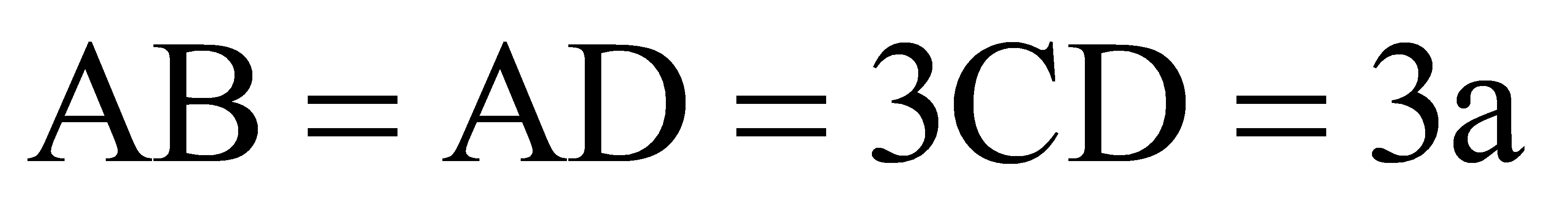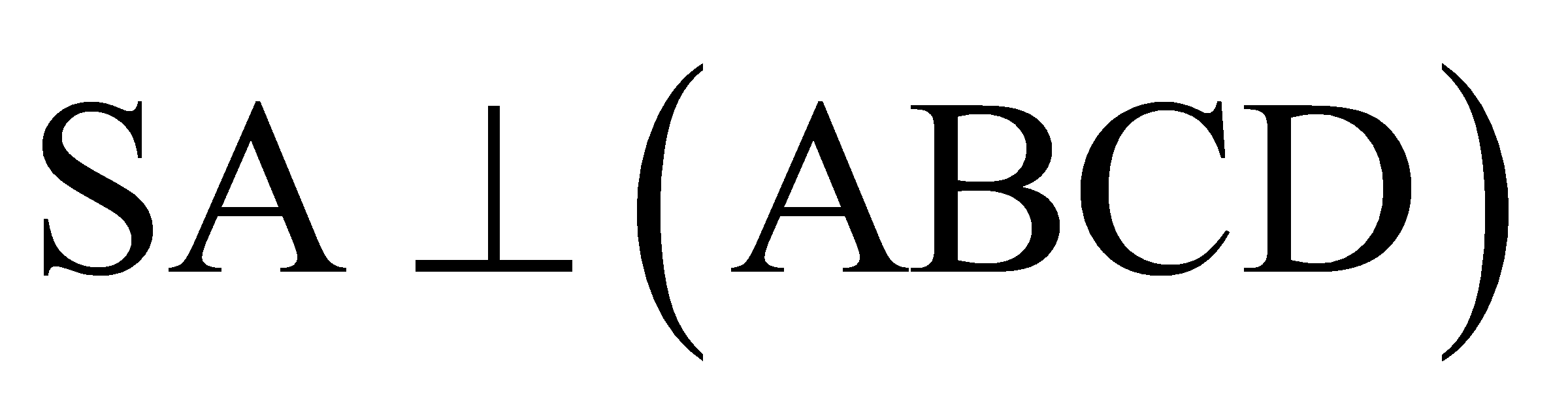và khoảng chừng cách từ điểm A đếnmp(SCD) bằng a. Tính thể tích của khối chóp S.ABCD.
Cho khối chóp
có cạnh bên 
vuông góc với đáy, đáy 
là hình chữ nhật, 
. Thế tích khối chóp 
bằng
Cho khối tứ diện ABCD có
, khoảng cách giữa hai đường thẳng AB và CD là 8cm, góc giữa hai đường thẳng AB và CD là 
.
Thể tích của khối tứ diện ABCD là:
Cho hìnhchópS.ABCcóđáyABClà tam giácvuôngtại A, mặtbênSABlà tam giácđềuvànằmtrongmặtphẳngvuônggócvớimặtphẳng (ABC), gọiMlàđiểmthuộccạnhSCsaochoMC = 2MS. Biết
, tínhkhoảngcáchgiữahaiđườngthẳngACvàBM?
Cho lăng trụ tam giác
có 
, góc giữa đường thẳng 
và 
bằng 
, tam giác 
vuông tại 
và góc 
. Hình chiếu vuông góc của điểm 
lên 
trùng với trọng tâm của 
. Thể tích của khối tứ diện 
theo 
bằng
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Cạnh bên SC phù phù hợp với đáy một góc
. Thể tích của khối chóp S.ABC là:
Cho hình chóp S.ABCD có đáy ABCDlà hình thoi tâm Ocạnh a, góc 
. Các mặt phẳng 
và 
cùng vuông góc với mặt đáy. Gọi Mlà trung điểm SD, thể tích khối chóp S.ABCD là 
. Hãy tính khoảng chừng cách htừ Mtới mặt phẳng 
theo a.
Cho hình chóp tứ giác đều
có cạnh đáy bằng a và mặt bên tạo với đáy một góc 
. Thể tích 
khối chóp 
là:
Cho hình chóp
có đáy là tam giác vuông tại 
, 
, 
. Cạnh bên 
và vuông góc với mặt phẳng 
. Thể tích khối chóp 
bằng:
Tínhthểtích V củakhốichóp S.ABC cóđộdàicáccạnh
Cho hình chóp 
có đáy 
là hình thang vuông tại 
và 
. Hai mặt phẳng 
và 
cùng vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng 
và 
bằng 
. Thểtích khối chóp 
bằng
Cho hình chóp 
có 
, góc giữa 
và 
là 
, 
đều cạnh 
. Thể tích khối chóp bằng
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, mặt bên tạo với đáy góc
. Thể tích khối chóp S.ABC là ?
Cho hình chóp tứ giác đều
, 
là giao điểm của 
và 
. Biết mặt bên của hình chóp là tam giác đều và khoảng chừng từ 
đến mặt bên là
. Tínhthểtíchkhốichóp
theo
.
Cho hình chóp tứ giác S.ABCDcó đáy là hình chữ nhất AB = a,
góc giữa SCvà đáy bằng 
. Thể tích của khối chóp S.ABCDbằng:
Cho hình chóp S.ABCD cóđáy ABCD là hình chữ nhật, hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) trùng với giao điểm O của hai tuyến đường chéo AC vàBD. Biết
, 
, 
, với M là trung điểm cạnh AB. Tính theo a thể tích khối chóp S.ABCD.
Cho hình chóp
sao cho 
,và chúng đôi một vuông góc với nhau. Khoảng cách từ 
đến mp
là
Khối chóp
có đáy 
là hình thoi cạnh 
. 
, Cạnh 
thay đổi. Thể tích lớn số 1 của khối chóp 
là:
Cho hình chóp
có đáy 
là tam giác đều cạnh 
, cạnh bên 
vuông góc với đáy. Tính thể tích khối chóp 
biết 
Cho hình chóp S.ABCD cóđáy ABCD là hình chữ nhật, hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) trùng với giao điểm O của hai tuyến đường chéo AC vàBD. Biết
, 
, 
, với M là trung điểm cạnh AB. Tính theo a thể tích khối chóp S.ABCD.
Cho hình lập phương
. I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
Cho hình nón đỉnh S có đường tròn đáy bán kính 1cm, nội tiếp trong hình vuông vắn ABCD. Biết 
cm. Tính thể tích của khối chóp S.ABCD
Cho lăng trụ ABC.A’B’C’ cóđáy ABC là tam giác đều cạnh a, và
. Thể tích khối lăng trụ ABC.A’B’C’ theo a là ?
Cho khốichópcóthểtích
vàdiệntíchmặtđáy
Tínhchiềucaocủakhốichóp.
Cho hình chóp lục giác đều SABCDEF có
. Tính thể tích khối chóp SABCDE.
Hình cóp S.ABC có đáy ABC là tam giác vuông cân (
), cạnh bên SA vuông góc với mặt phẳng đáy và có độ dài là 
, cạnh bên SB tạo với đáy một góc 
. Tính diện tích s quy hoạnh toàn phần của hình chóp.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng
. Tính thể tích khối chóp S.ABCD.
Khi tăng độ dài cạnh đáy của một khối chóp tam giác đều lên
lần và giảm độ cao của hình chóp đó đi 
lần thì thể tích khối chóp thay đổi ra làm sao?
Cho hình chóp S.ABCD có ABCD là hình vuông vắn cạnh a, SA vuông góc với mặt phẳng đáy (ABCD). Biết góc giữa SC và mặt phẳng (ABCD) bằng 60. Tính thể tích khối chóp S.ABCD.
Cho hình chóp
có đáy 
là hình vuông vắn cạnh bằng 
. Cạnh bện 
vuông góc với mặt phẳng 
và 
. Tính thể tích khối chóp 
.
Cho hình chóp tứgiác đều 
có cạnh đáy bằng 
. Gọi 
là vấn đề trên cạnh 
sao cho 
. Góc giữa 
và mặt phẳng đáy một góc 
. Tính thểtích 
của khối chóp 
.
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng
. Tính thể tích khối chóp S.ABC.
Cho hình chóp
có đáy ABC là tam giác vuông tại A,
,
, 
. SA vuông góc với đáy (ABC). Thể tích khối chóp 
là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông vắn cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450 và
. Tính thể tích V của khối chóp S.ABCD.
Cho khối chóp
có đáy 
là hình vuông vắn cạnh a, mặt bên 
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi M là trung điểm của cạnh SB. Tính thể tích V của khối chóp 
Cho hình tứ diện đều. Mệnh đề nào dưới đây sai?
Cho hình trụ có những đáy là hai tuyến đường tròn tâm
và 
, bán kính bằng độ cao bằng 
. Trên đường tròn đáy tâm 
lấy điểm 
, trên đường tròn tâm 
lấy điểm 
sao cho 
. Tính thể tích khối tứ diện 
theo 
?
Một số thắc mắc khác hoàn toàn có thể bạn quan tâm.
Cho
và 
là 3 cạnh của tam giác
. Số giá trị n thỏa mãn là ?
Tính giá trị của
.
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho biểu thức
, trong đó 
là phân số tối giản. Gọi 
. Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
Biểu thức
rút gọn là:
Với số dương
và những số nguyên dương 
, 
bất kì. Mệnh đề nào dưới đây đúng?
Giá trị của biểu thức
bằng
Rút gọn biểu thức
với 
?
Với
thì 
sẽ ra làm sao so với 
