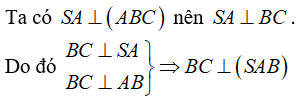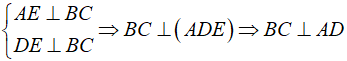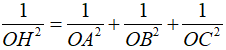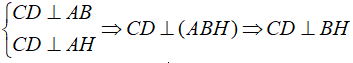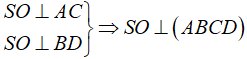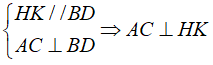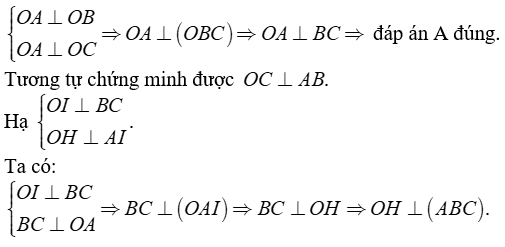Thủ Thuật về Cho hình chóp có đáy là hình vuông vắn tâm vuông góc với mặt phẳng gọi là trung điểm chọn xác định sai Mới Nhất
Dương Anh Sơn đang tìm kiếm từ khóa Cho hình chóp có đáy là hình vuông vắn tâm vuông góc với mặt phẳng gọi là trung điểm chọn xác định sai được Update vào lúc : 2022-04-04 22:25:13 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
 Tải app VietJack. Xem lời giải nhanh hơn!
Tải app VietJack. Xem lời giải nhanh hơn! Quảng cáo
* Cách chứng tỏ đường thẳng vuông góc với mặt phẳng cực hay
Muốn chứng tỏ đương thẳng d ⊥ (α) ta hoàn toàn có thể dùng môt trong hai cách sau.
Cách 1. Chứng minh d vuông góc với hai tuyến đường thẳng a; b cắt nhau trong (α) .
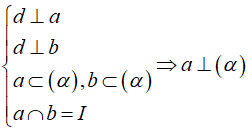
Cách 2. Chứng minh d vuông góc với đường thẳng a mà a vuông góc với (α) .
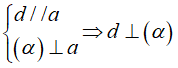
Cách 3. Chứng minh d vuông góc với (Q.) và (Q.) // (P).
* Chứng minh hai tuyến đường thẳng vuông góc
- Để chứng tỏ d ⊥ a, ta hoàn toàn có thể chứng tỏ bởi một trong những phương pháp sau:
+ Chứng minh d vuông góc với (P) và (P) chứa a.
+ Sử dụng định lí ba đường vuông góc.
+ Sử dụng những phương pháp chứng tỏ đã biết ở phần trước.
Ví dụ 1: Cho hình chóp S. ABC có SA ⊥ (ABC) và tam giác ABC vuông ở B , AH là đường cao của tam giác SAB. Khẳng định nào sau đây sai?
A. SA ⊥ BC
B. AH ⊥ BC
C. AH ⊥ AC
D. AH ⊥ SC
Hướng dẫn giải
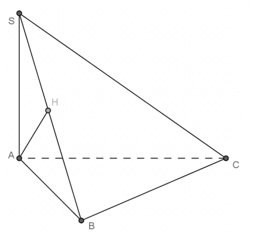
Chọn C

Vậy câu C sai.
Ví dụ 2: Cho tứ diện SABC có ABC là tam giác vuông tại B và SA ⊥ (ABC). Khẳng định nào sau đây là đúng nhất.

Hướng dẫn giải
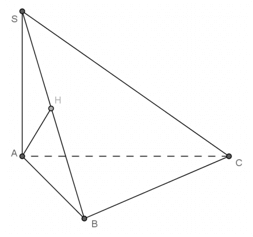
Chọn A
Quảng cáo
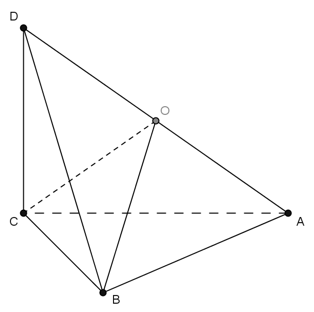
Ví dụ 3: Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
A. AB ⊥ (ABC)
B. AB ⊥ BD
C. AB ⊥ (ABD)
D. BC ⊥ AD
Hướng dẫn giải
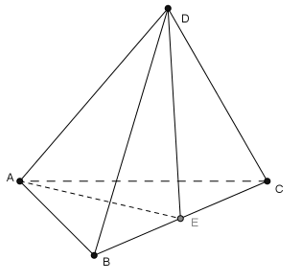
Chọn D
Gọi E là trung điểm của BC.
Tam giác DCB cân tại D có DE là đường trung tuyến nên đồng thời là đường cao: DE ⊥ BC.
Tam giác ABC cân tại A có AE là đường trung tuyến nên đồng thời là đường cao : AE ⊥ BC
Khi đó ta có
Ví dụ 4: Cho hình chóp S.ABC có SA ⊥ (ABC) và AB ⊥ BC Số những mặt của tứ diện S.ABC là tam giác vuông là:
A. 1 B. 2 C. 3 D. 4
Hướng dẫn giải
Có AB ⊥ BC ⇒ ΔABC là tam giác vuông tại B
Ta có SA ⊥ (ABC) ⇒ 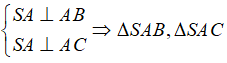
Mặt khác 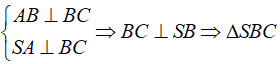
Vậy bốn mặt của tứ diện đều là tam giác vuông. Nên đáp án D đúng
Chọn D
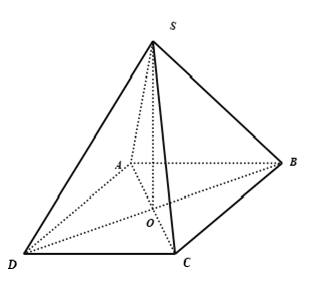
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
A. SO ⊥ (ABCD)
B. CD ⊥ (SBD)
C. AB ⊥ (SAC)
D. CD ⊥ AC
Hướng dẫn giải
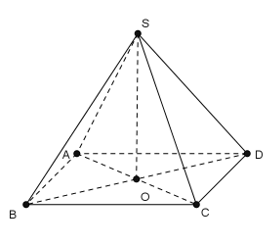
Chọn B
Tam giác SAC cân tại S có SO là trung tuyến nên SO cũng là đường cao ⇒ SO ⊥ AC .
Tam giác SBD cân tại S có SO là trung tuyến nên SO cũng là đường cao ⇒ SO ⊥ BD .
Từ đó suy ra SO ⊥ (ABCD) .
Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD)
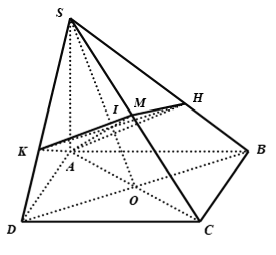
Ví dụ 6: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Gọi AE, AF lần lượt là những đường cao của tam giác SAB và tam giác SAD. Chọn xác định đúng trong những xác định sau ?
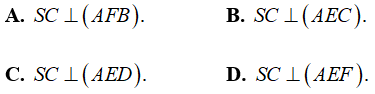
Quảng cáo
Hướng dẫn giải
Ta chứng tỏ phương án D đúng.
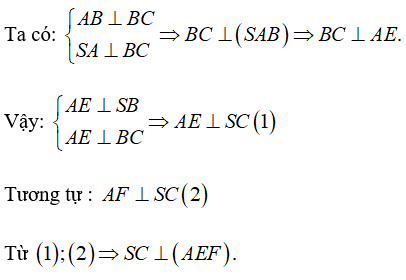
Chọn D
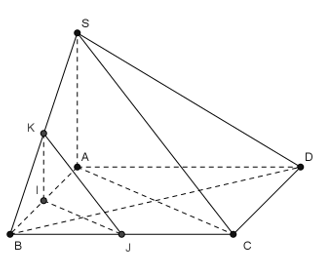
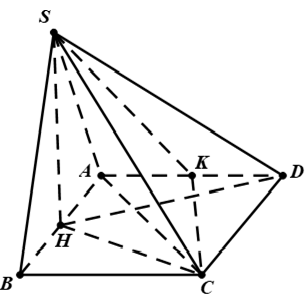
Ví dụ 7: Cho hình chóp S. ABC có cạnh SA ⊥ (ABC) và đáy ABC là tam giác cân ở C . Gọi H và K lần lượt là trung điểm của AB và SB . Khẳng định nào sau đây sai?
A. CH ⊥ SA B. CH ⊥ SB C. CH ⊥ AK D. AK ⊥ SB
Hướng dẫn giải
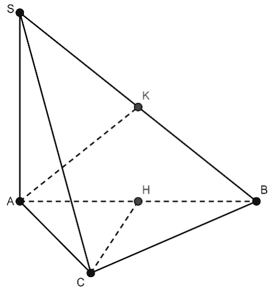
Chọn D
Do tam giác ABC cân tại C; có CH là đường trung tuyến nên đồng thời là đường cao nên CH ⊥ AB.
Lại có: CH ⊥ SA (vì SA vuông góc với mp(ABC)) .
Suy ra CH ⊥ (SAB). Vậy những câu A, B, C đúng nên D sai.
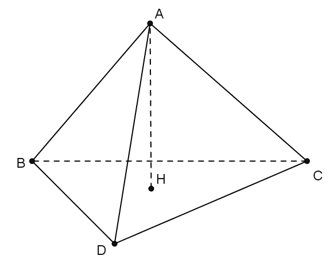
Ví dụ 8: Cho tứ diện ABCD. Vẽ AH ⊥ (BCD) . Biết H là trực tâm tam giac BCD. Khẳng định nào sau đây đúng?
A. CD ⊥ BD B. AC = BD C. AB = CD. D. AB ⊥ CD
Hướng dẫn giải
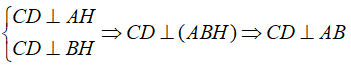
Chọn đáp án D
Ví dụ 9: Cho tứ diện SABC thoả mãn SA= SB= SC. Gọi H là hình chiếu của S lên mp (ABC) . Đối với tam giác ABC ta có điểm H là:
A. Trực tâm.
B. Tâm đường tròn nội tiếp.
C. Trọng tâm.
D. Tâm đường tròn ngoại tiếp.
Hướng dẫn giải
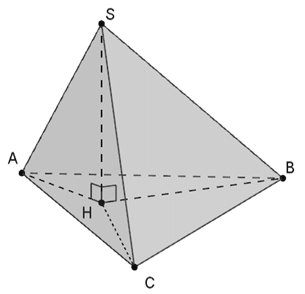
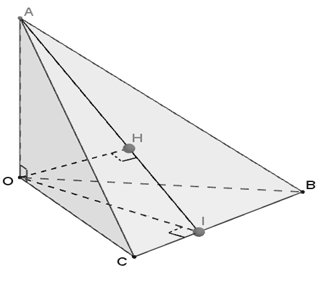
Ví dụ 10: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mp(ABC) . Mệnh đề nào sai trong những mệnh đề sau:
A. H là trực tâm tam giác ABC
B. H là tâm đường tròn ngoại tiếp tam giác ABC
C.
D. CH là đường cao của tam giác ABC .
Hướng dẫn giải
+ Ta có OA ⊥ (OBC) ⇒ OA ⊥ BC và OH ⊥ BC ⇒ BC ⊥ (OAH) ⇒ BC ⊥ AH. Tương tự, ta có AB ⊥ CH
Hai đường thẳng AH và CH cắt nhau tại H nên H là trực tâm tam giác ABC
suy ra đáp án A, D đúng
+ Gọi I là giao điểm của AH và BC .
Ta có ; OA ⊥ (OBC) nên OA ⊥ OI
Xét tam giác vuông OAI có đường cao OH Ta có
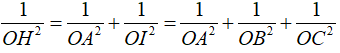
suy ra đáp án C đúng.
Chọn đáp án B
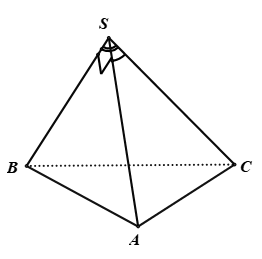
Ví dụ 11: Cho hình chóp S.ABC có ∠BSC = 120°, ∠CSA = 60°, ∠ASB = 90°, SA = SB = SC. Gọi I là hình chiếu vuông góc của S lên mp ( ABC). Chọn xác định đúng trong những xác định sau
A. I là trung điểm AB
B. I là trọng tâm tam giác ABC
C. I là trung điểm AC
D. I là trung điểm BC
Hướng dẫn giải
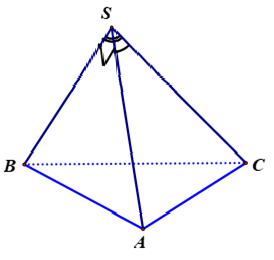
Gọi SA = SB = SC = a
+ Ta có : tam giác SAC đều nên AC = SA = a
Tam giác SAB vuông cân tại S ⇒ AB = a√2
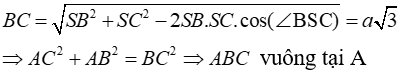
+ Gọi I là trung điểm của BC thì IA = IB = IC nên I là tâm
đường tròn ngoại tiếp tam giác ABC .
Ta có : SA = SB = SC và IA = IB = IC
⇒ SI là trục đường tròn ngoại tiếp tam giác ABC
⇒ SI ⊥ (ABC)
Vậy nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC)
Chọn D
Câu 1: Cho tứ diện ABCD có AB ⊥ CD và AC ⊥ BD. Gọi H là hình chiếu vuông góc của A lên mp(BCD) . Các xác định sau, xác định nào sai?
A. H là trực tâm tam giác BCD
B. CD ⊥ (ABH)
C. AD ⊥ BC
D. Các xác định trên đều sai.
Hiển thị lời giải
Ta có
Tương tự BD ⊥ CH
Suy ra H là trực tâm tam giác BCD. Suy ra loại đáp án A, B
Ta có 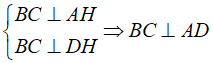
Chọn đáp án D
Câu 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H, K lần lượt là trực tâm những tam giác SBC và ABC. Mệnh đề nào sai trong những mệnh đề sau?
A. BC ⊥ (SAH) B. HK ⊥ (SBC)
C. BC ⊥ (SAB) D. SH, AK và BC đồng quy
Hiển thị lời giải
Ta có BC ⊥ SA, BC ⊥ SH ⇒ BC ⊥ (SAH)
Ta có CK ⊥ AB, CK ⊥ SA ⇒ CK ⊥ (SAB) hay CK ⊥ SB
Mặt khác có CH ⊥ SB nên suy ra SB ⊥ (CHK) hay SB ⊥ HK, tương tự SC ⊥ HK nên HK ⊥ (SBC)
Gọi M là giao điểm của SH và BC.
Do BC ⊥ (SAH) ⇒ BC ⊥ AM hay đường thẳng AM trùng với đường thẳng AK
⇒ SH, AK và BC đồng quy
Do dó BC ⊥ (SAB). Sai
Chọn đáp án C
Câu 3: Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây là sai?.
A. SO ⊥ (ABCD)
B. SO ⊥ AC
C. SO ⊥ BD
D. Cả A, B, C đều sai
Hiển thị lời giải
Ta có O là trung điểm của AC và SA = SC ⇒ SO ⊥ AC
Tương tự SO ⊥ BD
Vậy
Chọn D
Câu 4: Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, SA ⊥ (ABCD). Các xác định sau, xác định nào sai?
A. SA ⊥ BD B. SC ⊥ BD C. SO ⊥ BD D. AD ⊥ SC
Hiển thị lời giải
Ta có SA ⊥ (ABCD) ⇒ SA ⊥ BD
Do tứ giác ABCD là hình thoi nên BD ⊥ AC mà SA ⊥ BD nên BD ⊥ (SAC) hay BD ⊥ SC, BD ⊥ SO
Chọn đáp án D
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông vắn và SA ⊥ (ABCD). Gọi I; J; K lần lượt là trung điểm của AB, BC và SB. Khẳng định nào sau đây sai?
A. (IJK) // (SAC)
B. BD ⊥ (IJK)
C. Góc giữa SC và BD có số đo 60°
D. BD ⊥ (SAC)
Hiển thị lời giải
Chọn C.
+ Tam giác ABC có IJ Là đường trung bình của tam giác nên IJ // AC
Tam giác SAB có IK là đường trung bình của tam giác nên IK // SA
⇒ (IJK) // (SAC). Vậy A đúng
+ Do BD ⊥ AC và BD ⊥ SA nên BD ⊥ (SAC)
nên D đúng.
+ Do BD ⊥ (SAC) và (IJK) // (SAC) nên BD ⊥ (IJK) nên B đúng.
Vậy C sai
Câu 6: Cho hình chóp S. ABCD có đáy ABCD là hình vuông vắn, Gọi H là trung điểm của AB và SH ⊥ (ABCD). Gọi K là trung điểm của cạnh AD. Khẳng định nào sau đây là sai?
A. AC ⊥ SH
B. AC ⊥ KH
C. AC ⊥ (SHK)
D. Cả A, B, C đều sai
Hiển thị lời giải
+ Ta cos SH ⊥ (ABCD) ⇒ SH ⊥ AC
+ Tam giác ABD có H và K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của tam giác ⇒ HK // BD
Lại có
⇒ AC ⊥ (SHK)
Chọn D
Câu 7: Cho tứ diện OABC có ba cạnh OA ; OB ; OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Khẳng định nào sau đây sai?
 Hiển thị lời giải
Hiển thị lời giải
Xét tam giác AOI vuông tại O có OH đường cao:
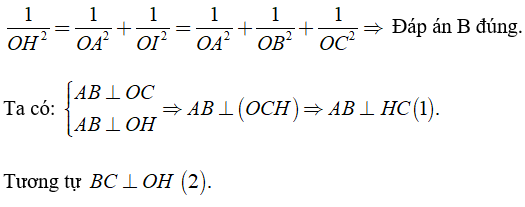
Từ (1) và (2) ⇒ H là trực tâm tam giác ABC ⇒ Đáp án C đúng.
Chọn đáp án D.
Câu 8: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc nhau. Hãy chỉ ra điểm O cách đều bốn điểm A, B ; C ; D.
A. O là tâm đường tròn ngoại tiếp tam giác ABC
B. O là trọng tâm tam giác ACD
C. O là trung điểm cạnh BD
D. O là trung điểm cạnh AD
Hiển thị lời giải
Chọn D

Câu 9: Cho tứ diện ABCD. Vẽ AH ⊥ (BCD). Biết H là trực tâm tam giác BCD . Khẳng định nào sau đây không sai?
A. AB = CD B. AC = BD C. AB ⊥ CD D. CD ⊥ BB
Hiển thị lời giải
Chọn C
Do AH ⊥ (BCD) ⇒ AH ⊥ CD .
Mặt khác, H là trực tâm tam giác BCD nên BH ⊥ CD
Suy ra CD ⊥ (ABH) nên CD ⊥ AB.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông vắn cạnh a, mặt bên SAB là tam giác đều và SC = a√2. Gọi H, K lần lượt là trung điểm của những cạnh AB và AD. Khẳng định nào sau đây là sai?.
A. SH ⊥ (ABCD)
B. SH ⊥ HC
C. A, B đều đúng
D. A, B là sai
Hiển thị lời giải
Vì H là trung điểm của AB và tam giác SAB đều nên SH ⊥ AB
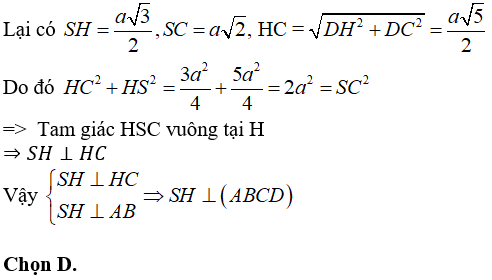
Câu 11: Cho hình lập phương ABCD.A'B'C'D'. Đường thẳng AC’ vuông góc với mặt phẳng nào sau đây?
A. ( A’BD) B. ( A’DC’) C. ( A’CD’) D. ( A’B’CD)
Hiển thị lời giải
Ta có
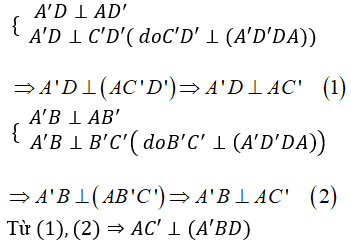
Vậy chọn đáp án A
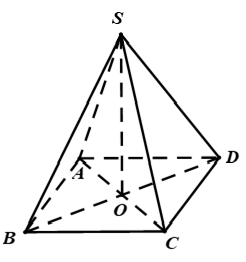
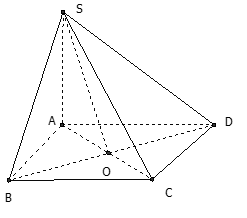
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA = SC. Các xác định sau, xác định nào đúng?
A. SA ⊥ (ABCD) B. BD ⊥ (SAC)
C. AC ⊥ (SBD) D. AB ⊥ (SAC)
Hiển thị lời giải
Ta có: SA = SC nên tam giác SAC là tam giác cân
Mặt khác: O là trung điểm của AC (tính chất hình thoi)
Khi đó ta có: AC ⊥ SO
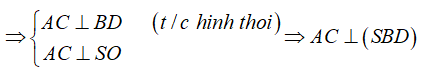
Vậy chọn đáp án C
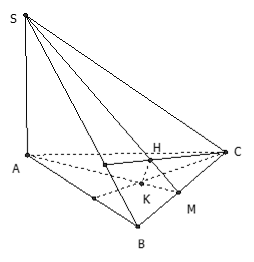
Câu 13: Cho hình chóp S. ABCD có đáy ABCD là hình vuông vắn, SA ⊥ (ABCD). Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K . Chọn xác định sai trong những xác định sau?
A. AK ⊥ HK B. HK ⊥ AM C. BD // KH D. AH ⊥ SB .
Hiển thị lời giải
Câu 14: Cho hình chóp S.ABC có ∠BSC = 120°, ∠CSA = 60°, ∠ASB = 90°, SA = SB = SC. Gọi I là hình chiếu vuông góc của S lên mp(ABC). Chọn xác định đúng trong những xác định sau
A. I là trung điểm AB
B. I là trọng tâm tam giác ABC
C. I là trung điểm AC
D. I là trung điểm BC
Hiển thị lời giải
Gọi SA = SB = SC = a
Ta có: tam giác SAC cân có một góc bằng 60° nên tam giác SAC đều ⇒ AC = SA = a
+ tam giác SAB vuông cân tại S
⇒ AB = a√2
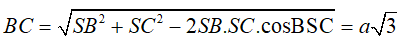
⇒ AC2 + AB2 = BC2 nên tam giác ABC vuông tại A
+ Gọi I là trung điểm của AC thì I là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là trục của tam giác ABC thì d đi qua I và d ⊥ (ABC)
Mặt khác : SA = SB = SC nên S ∈ d . Vậy SI ⊥ (ABC) nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC)
Chọn C
Câu 15: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng ( ABC) . Xét những mệnh đề sau :
I. Vì OC ⊥ OA, OC ⊥ OB nên OC ⊥ (OAB)
II. Do AB ⊂ (ABC) nên AB ⊥ OC (1)
III. Có OH ⊥ (ABC) và AB ⊂ (ABC) nên AB ⊥ OH (2)
IV. Từ (1) và (2) AB ⊥ (OCH)
Trong những mệnh đề trên mệnh đề nào đúng ?
A. I, II, III, IV
B. I, II, III
C. II, III, IV
D. I, IV
Hiển thị lời giải
Ta có:

Chọn đáp án A
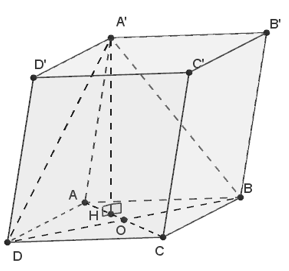
Câu 16: Cho hình hộp ABCD.A’B’C’D’ Có đáy là hình thoi ∠BAD = 60° và AA’ = A’B = A’D. Gọi O = AC ∩ BD. Hình chiếu của A’ trên (ABCD) là :
A. trung điểm của AO
B. trọng tâm tam giác ABD
C. giao của hai đoạn AC và BD
D. trọng tâm tam giác BCD.
Hiển thị lời giải
Vì A’A = A’B = A’D nên hình chiếu của A’ trên ( ABCD) trùng với H là tâm đường tròn ngoại tiếp tam giác ABD (1).
Mà tứ giá ABCD là hình thoi và ∠BAD = 60° nên tam giác BAD là tam giác đều (2)
Từ (1) và ( 2) suy ra H là trọng tâm tam giác ABD
Chọn đáp án B
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
 Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!
Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù phù hợp với nội quy phản hồi trang web sẽ bị cấm phản hồi vĩnh viễn.
[embed]https://www.youtube.com/watch?v=If56GnsX5V0[/embed]