Mẹo về Trong những dãy số sau dãy số nào là dãy số bị chặn a 2 1 1 nnun b 2 sin nunn c 2 nun d 3 1 nun 2022
Họ và tên học viên đang tìm kiếm từ khóa Trong những dãy số sau dãy số nào là dãy số bị chặn a 2 1 1 nnun b 2 sin nunn c 2 nun d 3 1 nun được Update vào lúc : 2022-07-19 21:58:03 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.
1 SỞ GD&ĐT HÀ N ỘI TRƯỜNG THPT YÊN HOÀ ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II, NĂM HỌC 2022-2022 MÔN: TOÁN, KHỐI: 11 PH ẦN I. TR ẮC NGHI ỆM I. DÃY SỐ Câu 1. Số hạng tổng quát của dãy số n u viết dư ới dạng khai triển 111 1; ; ; ;... 234 là: A. 1 . 2 n u n B. 1 . n u n C. 2 1 . n u n D. 1 . 1 n u n Câu 2. Cho dãy số n u , biết 31 n n n u . Ba số hạng đ ầu của dãy số đó là: A. 1 1 1 ; ; . 2 4 8 B. 1 1 1 ; ; . 2 4 16 C. 1 1 3 ; ; . 2 4 26 D. 1 2 3 ; ; . 234 Câu 3. Cho dãy số () n u xác đ ịnh bởi: 1 1 1 2 3 2 nn u u u n . Viết năm s ố hạng đ ầu của dãy; A. 1;5;13;28;61 B. 1;5;13;29;61 C. 1;5;17;29;61 D. 1;5;14;29;61 Câu 4. Cho dãy số n u , biết 1 1 5 nn u u u n với 1 n . Số hạng tổng quát của dãy số đó là: A. 1 . 2 n nn u B. 1 5. 2 n nn u C. 1 5. 2 n nn u D. 12 5. 2 n nn u Câu 5. Cho dãy số n u , biết 1 21 n n u n . Số 8 15 là số hạng thứ mấy của dãy số? A. 8. B. 6. C. 5. D. 7. Câu 6. Cho dãy số n u , biết 23 1 () 1 n n n u n . Số hạng 1 n u là: A. 2( 1) 3 1 1 () 1 n n n u n B. 2( 1) 3 1 1 () 2 n n n u n C. 23 1 () 2 n n n u n D. 25 1 () 2 n n n u n Câu 7. Cho dãy số n u có số hạng tổng quát là 2.3 n n u . Công thức truy hồi của dãy số đó là? A. 1 1 6 6 ,n 2 nn u uu B. 1 1 6 3 ,n 2 nn u uu C. 1 1 3 3 ,n 2 nn u uu D. 1 1 3 6 ,n 2 nn u uu Câu 8. Cho dãy số n u , biết 1 1 3 1 ,1 2 nn u u u n . Mệnh đ ề nào sau đây sai? A. 1 2 3 4 5 93 u u u u u 16 . B. 10 3 u 512 . C. n 1 n n 9 uu 2 . D. n n 3 u 2 . . Câu 9. Trong những dãy số n u cho bởi số hạng tổng quát n u sau, dãy số nào là dãy số tăng? A. 1 . 2 n n u B. 1 . n u n C. 5 . 31 n n u n D. 21 . 1 n n u n Câu 10. Trong những dãy số n u cho bởi số hạng tổng quát n u sau, dãy số nào là dãy số giảm? A. 1 . 2 n n u B. 31 . 1 n n u n C. 2 . n un D. 2. n un Câu 11. Trong những dãy số n u cho bởi số hạng tổng quát n u sau, dãy số nào bị chặn trên? 2 A. 2 . n un B. 2. n n u C. 1 . n u n D. 1. n un Câu 12. Cho dãy số n u có 2 1 n u n n . Khẳng đ ịnh nào sau đây là sai? A. 4 số hạng đ ầu của dãy là: 1; 1; 5; 11 . B. 2 1 1 n u n n . C. Là một dãy số tăng . D. 1 2 nn u u n . Câu 13. Xét tính bị chặn của những dãy số n u , biết : 1 1 1 ... 1.3 2.4 .( 2) n u nn A. Không bị chặn B. Bị chặn C. Bị chặn trên D. Bị chặn dư ới Câu 14. Cho dãy số n u , biết sin cos n u n n . Dãy số n u bị chặn dư ới bởi A. 1. B. 2. C. 1 . 2 D. 2. Câu 15. Trong những dãy số có số hạng tổng quát sau, hãy lựa chọn dãy bị chặn. A. 1 n un n B. 32 n u n n C. 32 n n u D. 2 1 n n u n II. CẤP SỐ CỘNG Câu 1. Xen Một trong những số 2 và 22 ba số để được một cấp số cộng có 5 số hạng. Chọn đáp án đúng A. 7;12;17. B. 6,10,14. C. 8,13,18. D.Tất cả đều sai Câu 2. Trong những dãy số n u cho bởi số hạng tổng quát n u sau, dãy số nào không phải là cấp số cộng: A. 5 2 . n un B. 2. n n u C. 3. 2 n n u D. 23 . 5 n n u Câu 3. Cho cấp số cộng n u biết : 1 3 5 16 10 17 u u u uu , khi đó u 1 bằng: A. 1 16. u B. 1 6. u C. 1 7. u D. 1 14. u Câu 4. Cho cấp số cộng n u có 2 d và 8 2 7 S , khi đó 1 u bằng: A. 1 1 . 1 6 u B. 1 16 . u C. 1 1 . 16 u D. 1 16. u Câu 5. Cho cấp số cộng n u có: 1 11 , 44 ud . Chọn khẳng đ ịnh đúng trong những kh ẳng đ ịnh sau đây? A. 5 5 . 4 S B. 5 4 . 5 S C. 5 5 . 4 S D. 5 4 . 5 S Câu 6. Cho cấp số cộng n u có: 1 1, 2, 483 n u d s . Hỏi cấp số cộng có bao nhiêu số hạng? A. 21. n B. 23. n C. 22. n D. 20. n Câu 7. Cho cấp số cộng có 4 14 12, 18 uu . Khi đó s ố hạng đ ầu tiên và công sai là A. 1 21, 3. ud B. 1 20, 3. ud C. 1 22, 3. ud D. 1 21, 3. ud Câu 8. Xác đ ịnh xđể 3 số 2 1 , ,1 x x x lập thành một cấp số cộng. A. 1 x hoặc 1 x B. 2 x hoặc 2. x C. Không có mức giá trị nào của x. D. 0. x Câu 9. Cho , , abc lập thành một cấp số cộng. Đ ẳng thức nào sau đây là đúng? A. 22 . a c ab bc B. 22 2 2 . a c ab bc C. 2 2 2 2 4 . a c ac b D. 22 2 2 . a c ab bc Câu 10. Cho cấp số cộng có u 2 + u 22 = 60. Tổng 23 số hạng đ ầu tiên là: A.690 B.680 C.600 D.500 Câu 11. Cho cấp số cộng (u n ) thỏa mãn 25 3 10 42 66 uu uu . Tổng của 346 số hạng đ ầu là: A.242546 B.242000 C.241000 D.240000 3 Câu 12. Cho cấp số cộng (u n ) có công sai 0 d ; 31 34 22 31 34 11 101 uu uu . Hãy tìm số hạng tổng quát của cấp số cộng . A. 39 n un B. 32 n un C. 3 92 n un D. 3 66 n un Câu 13. Cho dãy số n u : 1 1 3 5 ; - ; - ; - ;... 2222 Khẳng đ ịnh nào sau đây sai? A. (u n ) là một cấp số cộng. B. (u n ) là một dãy giảm C. Số hạng 20 19,5 u . D. Tổng của 20 số hạng đ ầu tiên là 180 . Câu 14. Ba góc A,B,C (A
VnHocTap.com ra mắt đến những em học viên lớp 11 nội dung bài viết Xét tính bị chặn của dãy số, nhằm mục đích giúp những em học tốt chương trình Toán 11.
Nội dung nội dung bài viết Xét tính bị chặn của dãy số: Để chứng tỏ dãy số (n) bị chặn trên bởi M, ta chứng tỏ cun • M, Vn thuộc N*. Để chứng tỏ dãy số (un) bị chặn dưới bởi m, ta chứng tỏ La > m, n c N*. Để chứng tỏ dãy số bị chặn ta chứng tỏ nó bị chặn trên và bị chặn dưới. Nếu dãy số (un) tăng thì bị chặn dưới bởi ad1. Nếu dãy số (1) giảm thì bị chăn trên bởi t.
Ví dụ 1. Chứng minh rằng dãy số (un) với n = 3n bị chặn trên bởi. Vậy dãy số đã cho bị chặn. Ví dụ 2. Chứng minh rằng dãy số (un) xác định bởi un = 3n + 5 là một dãy số bị chặn. Ta có up > 0, V3 > 1. Suy ra dãy số bị chặn dưới. Ví dụ 3. Trong những dãy số (un) sau, dãy số nào bị chặn trên, bị chặn dưới và bị chặn? a) Ta có m > 1 nên n > 2. Do đó dãy số đã cho bị chặn dưới bởi 2 và không biến thành chặn trên. b) Ta có 0 < n 0. Dãy (n) bị chặn trên bởi 0 và không biến thành chặn dưới. e) Dãy số không biến thành chặn trên, không biến thành chặn dưới.
Ví dụ 4. Cho dãy số (1) xác định bởi 1 = 0 và 2 + 1, Vn >1. a) Chứng minh dãy (n) bị chặn trên bởi số 8. b) Chứng minh dãy (un) tăng, từ đó suy ra dãy (19) bị chặn. a) Ta chứng tỏ den 1. Khi m = 1, ta có t1 = 0 < 8. Giả sử n 1, tức là i < 8. Ta cần chứng tỏ 2k + 1 <8.> 1, ta có 2n + 1 – 2n = 4 – cun. Mà cun 58 nên n + 1 – (n > 0. Suy ra đun là dãy số tăng. Do đó (n) bị chặn dưới bởi 11 = 0. Kết phù phù hợp với câu a, ta được dãy số (1) bị chặn.
BÀI TẬP TỰ LUYỆN: Bài 1. Trong những dãy SỐ (n) sau, dãy số nào bị chặn trên, bị chặn dưới và bị chặn? a) Dãy số bị chặn dưới bởi 6, không biến thành chặn trên. b) Dãy (n) bị chặn dưới bởi 0. Vì n < 8 nên dãy số bị chặn trên. c) Ta có dung <1>
Đáp án D
Xét đáp án A:
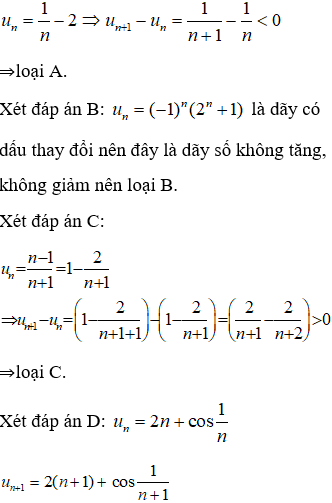
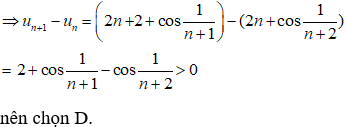
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Tải app VietJack. Xem lời giải nhanh hơn! Quảng cáo
1) Nếu số hạng tổng quát cho dưới dạng
thì:
Thu gọn un, nhờ vào biểu thức thu gọn để chặn un.
Ta cũng hoàn toàn có thể chặn tổng
bằng một tổng mà ta hoàn toàn có thể biết được chặn trên, chặn dưới của nó.
2) Nếu dãy số (un) cho bởi một hệ thức truy hồi thì:
Dự đoán chặn trên, chặn dưới rồi chứng tỏ bằng phương pháp chứng tỏ quy nạp.
Ta cũng hoàn toàn có thể xét tính đơn điệu (nếu có) sau đó giải bất phương trình un+1 − un nhờ vào đó chặn (un).
3) Nếu số hạng tổng quát cho bởi công thức thì ta nhờ vào phương pháp đánh giá (để ý quan tâm n ∈ N*)
Ví dụ 1: Xét tính bị chặn của những dãy số (un) có
A. Bị chặn B. Không bị chặn C. Bị chặn trên D. Bị chặn dưới
Hướng dẫn giải:
* Với n∈ N* ta có :
Nên dãy số bị chặn dưới bởi 0
+ Lại có;
với n ∈ N*
Nên dãy (un) bị chặn trên bởi 2.
=> dãy số (un)bị chặn.
Chọn A.
Ví dụ 2: Xét tính bị chặn của những dãy số (un) biết un = (−1)n
A. Bị chặn B. Không bị chặn C. Bị chặn trên D. Bị chặn dưới
Hướng dẫn giải:
Ta có:
=> − 1 ≤ un ≤ 1 với mọi n nên (un) là dãy số bị chặn.
Chọn A.
Quảng cáo
Ví dụ 3: Xét tính bị chặn của những dãy số (un) biết un = 4n − 2
A. Bị chặn B. Không bị chặn C. Bị chặn trên D. Bị chặn dưới
Hướng dẫn giải:
Ta có n ≥ 1 nên 4n − 2 ≥ 2
=> dãy số (un) bị chặn dưới bởi 2 và dãy (un) không biến thành chặn trên.
Chọn D.
Ví dụ 4: Cho dãy số (un) xác định bởi
. Chọn mệnh đề sai. A. Dãy số (un) bị chặn trên.
B.Dãy số (un) bị chặn dưới.
C. Dãy số tăng.
D. Dãy số không biến thành chặn.
Hướng dẫn giải:
+ Xét hiệu:
Vậy (un) là dãy số tăng.
+ Ta có:
suy ra ∀n ∈ N*; un < 2 nên (un) bị chặn trên. (1)
Vì (un) là dãy số tăng nên
=> (un) bị chặn dưới. (2)
Từ (1) và (2) suy ra (un) bị chặn.
=> D sai.
Chọn D.
Ví dụ 5: Cho dãy số (un) xác định bởi un = 1 + (n − 1) . 2n. Chọn mệnh đề sai.
A. Dãy số tăng.
B. Công thức truy hồi của dãy số là:
C. 5 số hạng đầu tiên của dãy số là một trong,5,17, 49, 129.
D. Dãy số bị chặn trên.
Hướng dẫn giải:
+ Ta có:
=> C đúng
+ Xét hiệu:
Vậy công thức truy hồi:
+ Ta có: un+1 − un = (n+1). 2n > 0
Suy ra dãy số (un) là dãy số tăng.
Ta có: un = 1 + (n − 1).2n ≥ 1 với ∀n ≥ 1
=> (un) là dãy số bị chặn dưới.
=> D sai.
Chọn D.
Quảng cáo
Ví dụ 6: Cho dãy số (un) xác định bởi
. Chọn mệnh đề đúng.
A. Dãy số (un) bị chặn trên ; không biến thành chặn dưới.
B. Dãy số (un) bị chặn dưới ; không biến thành chặn trên.
C.Dãy số (un) không biến thành chặn.
D. Dãy số (un) bị chặn.
Hướng dẫn giải:
Công thức un được viết lại:
Với mọi n ∈ N* ta có : 2n2 + 4 > 0
=> (un) bị chặn trên bởi
+ Lại có : với mọi n ∈ N* thì : n2 + 1 > 0 và 2n2 + 4 > 0
=>(un) bị chặn dưới bởi 0.
Vậy dãy số (un) là bị chặn
Chọn D.
Ví dụ 7: Cho dãy số (un) xác định bởi
. Chọn mệnh đề sai.
A. Dãy số tăng.
B. Dãy số bị chặn trên.
C. Dãy số bị chặn dưới nhưng không biến thành chặn trên.
D.Dãy số bị chặn.
Hướng dẫn giải:
* Ta viết lại:
Xét hiệu số:
Vậy dãy số (un) là dãy số tăng.
* Ta có:
Suy ra (un) là một dãy số bị chặn.
Kết luận (un) là một dãy số tăng và bị chặn.
Chọn C.
Ví dụ 8: Cho dãy số (un) được xác định bởi un = n2 − 4n + 3. Tìm mệnh đề sai.
A. Công thức truy hồi của dãy số là :
B. Dãy số bị chặn dưới.
C. Tổng n số hạng đầu tiên của dãy số là
D. Dãy số bị chặn trên.
Hướng dẫn giải:
* Ta có: u1 = 12 − 4.1 + 3 = 0
Xét hiệu:
Vậy công thức truy hồi:
* Ta có: un = n2 − 4n + 4 − 1 = (n − 2)2 − 1 ≥ 1 với ∀n ≥ 1
Vậy dãy số bị chặn dưới, nhưng không biến thành chặn trên.
*Ta có:
Chọn D.
Ví dụ 9: Cho dãy số (un) xác định bởi
. Tìm mệnh đề đúng nhất ?
A. Dãy số bị chặn trên ; không biến thành chặn dưới.
B. Dãy số bị chặn dưới ; không biến thành chặn trên.
C. Dãy số không biến thành chặn.
D. Dãy số bị chặn.
Hướng dẫn giải:
+ Rõ ràng un > 0 với mọi n nên (un) bị chặn dưới bởi 0.
+ Lại có:
Suy ra:
=> (un) bị chặn trên.
Kết luận (un) bị chặn.
Chọn D.
Ví dụ 10: Cho dãy số (un) xác định bởi
. Chọn mệnh đề đúng ?
A. Dãy số bị chặn.
B. Dãy số bị chặn trên nhưng không biến thành chặn dưới.
C. Dãy số bị chặn dưới nhưng không biến thành chặn trên.
D. Dãy số không biến thành chặn .
Hướng dẫn giải:
* Rõ ràng un > 0 với ∀n ∈ N* nên (un) bị chặn dưới bởi 0.
* Có
. Do đó:
với mọi n.
=> (un) bị chặn trên bởi 2.
Kết luận (un) bị chặn.
Chọn A.
Ví dụ 11: Xét tính tăng, giảm và bị chặn của dãy số (un) biết
A. Dãy số tăng, bị chặn trên B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn trên D. Cả A, B, C đều sai
Hướng dẫn giải:
* Với mọi n ∈ N* ; ta có un > 0. Xét tỉ số
=> un+1 < un nên dãy (un) là dãy số giảm.
* Vì dãy số (un) là dãy số giảm nên un ≤ u1 = 2 ∀n
Suy ra: 0 < un ≤ 2 ∀n ∈ N*
=> dãy (un) là dãy bị chặn.
Chọn D .
Ví dụ 12: Cho dãy số
. Xét dãy số yn = xn+1 − xn. Khẳng định nào đúng về dãy (yn)
A. Tăng,bị chặn B. Giảm,bị chặn
C. Tăng,chặn dưới D. Giảm,chặn trên
Hướng dẫn giải:
Ta có:
Do đó:
Ta chứng tỏ dãy (yn) tăng.
Ta có:
Ta chứng tỏ dãy (yn) bị chặn.
Trước hết ta chứng tỏ: xn ≤ 4(n−1) (1) với n ≥ 2
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2.
* Giả sử (1) đúng với n = k, tức là: xk ≤ 4(k−1). Ta chứng tỏ đúng với n = k + 1
Nên (1) đúng với n= k+1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có:
Vậy bài toán được chứng tỏ.
Câu 1: Xét tính bị chặn của dãy số (un): un = 4 − 3n − n2
A. Bị chặn B. Không bị chặn
C. Bị chặn trên D. Bị chặn dưới
Hiển thị đáp án
Đáp án: C
Ta có
=> dãy số (un) bị chặn trên; dãy (un) không biến thành chặn dưới.
Câu 2: Xét tính bị chặn của dãy số (un) biết
A. Bị chặn B. Không bị chặn
C. Bị chặn trên D. Bị chặn dưới
Hiển thị đáp án
Đáp án: A
Ta có:
+ Với mọi n ∈ N* ta có 2n > 0 và n2 − n + 1 > 0
nên un > 1 (1)
+ Áp dụng bất đẳng thức Cô- si ta được: n2 + 1 ≥ 2n
=> n2 − n + 1 ≥ n nên
=> un ≤ 3 (2).
Từ (1) và (2) suy ra dãy số (un) là bị chặn.
Câu 3: Xét tính bị chặn của dãy số (un) biết
A. Bị chặn B. Không bị chặn
C. Bị chặn trên D. Bị chặn dưới
Hiển thị đáp án
Đáp án: A
* Với mọi n nguyên dương ta có:
* Lại có:
với mọi n ∈ N*
Vậy 0 < un ≤ 2 nên dãy số (un) là dãy số bị chặn.
Câu 4: Cho dãy số (un) xác đinh bởi
. Tìm mệnh đề đúng?
A. Dãy số bị chặn trên. B. Dãy số bị chặn dưới.
C. Dãy số bị chặn. D. Dãy số không biến thành chặn.
Hiển thị đáp án
Đáp án: C
* Với mọi n ∈ N* ta có: un > 0
=> (un) bị chặn dưới bởi 0.
Lại có:
Suy ra
=> (un) bị chặn trên bởi
Kết luận (un) bị chặn.
Câu 5: Cho dãy số (un) xác đinh bởi
. Tìm mệnh đề sai?
A. Dãy số bị chặn
B. Dãy số bị chặn trên; không biến thành chặn dưới.
C. Dãy số bị chặn dưới; không biến thành chặn trên.
D. Dãy số không biến thành chặn.
Hiển thị đáp án
Đáp án: A
+ Với mọi n ∈ N* ta có un > 0 nên dãy số bị chặn dưới bởi 0.
+ Lại có:
Suy ra:
Nên (un) bị chặn trên.
Kết luận (un) bị chặn.
Câu 5: Cho dãy số (un) xác đinh bởi
. Tìm mệnh đề sai?
A. Với mọi n ∈ N*; un < 15
B. Dãy số (un) là dãy số tăng.
C. Dãy số (un) bị chặn dưới.
D. Dãy số (un) bị chặn.
Hiển thị đáp án
Đáp án: D
* Ta dùng quy nạp chứng tỏ: với mọi n ∈ N*; un < 15
Ta có u1 = 1 < 15 nên đúng với n= 1.
Giả sử đúng với n = k; k ∈ N* tức là có: uk < 15.
khi đó
Vậy un < 15 với ∀n ∈ N*. (1)
* Ta có
(do (1))
=> dãy số (un) tăng
=> un ≥ u1 = 1 nên (un) bị chặn dưới bởi 1.
Câu 6: Cho dãy số (un) xác đinh bởi
. Tìm mệnh đề đúng?
A. Dãy số bị chặn trên nhưng không biến thành chặn dưới.
B. Dãy số bị chặm dưới nhưng không biến thành chặn trên.
C. Dãy số bị chặn.
D. Dãy số không biến thành chặn.
Hiển thị đáp án
Đáp án: C
*Với k = 2,3...n ta có
Do đó:
Vế cộng vế suy ra:
=>(un) bị chặn trên bởi 2.
* Mặt khác; với ∀n ∈ N* ta có: un > 0
=> (un) bị chặn dưới bởi 0.
=> (un) bị chặn.
Câu 7: Cho dãy số (un) xác đinh bởi
. Tìm mệnh đề đúng trong những mệnh đề sau .
A. Dãy số (un) bị chặn.
B.Dãy số (un) không biến thành chặn .
C. Dãy số (un) bị chặn trên nhưng không biến thành chặn dưới.
D. Dãy số (un) bị chặn dưới nhưng không biến thành chặn trên.
Hiển thị đáp án
Đáp án: A
*Với mọi n∈ N* ta có:
nên (un) bị chặn dưới bởi 0.
* Lại có:
Mà:
Suy ra: un < 3 với mọi n nên dãy số (un) bị chặn trên bởi 3.
Kết luận: dãy số (un) bị chặn.
Câu 8: Xét tính tăng, giảm và bị chặn của dãy số (un) biết
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không biến thành chặn
D. Cả A, B, C đều sai
Hiển thị đáp án
Đáp án: A
* Ta có:
với mọi n ≥ 1.
Suy ra un+1 > un ∀n ≥ 1 ⇔ dãy (un) là dãy tăng.
* Mặt khác:
Với n ≥ 1; thì
Lại có với n ≥ 1 thì
Suy ra:
Vậy dãy (un) là dãy bị chặn.
Câu 9: Xét tính tăng, giảm và bị chặn của dãy số (un) biết
A. Dãy số tăng, bị chặn trên B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn trên D. Cả A, B, C đều sai
Hiển thị đáp án
Đáp án: B
* Ta có:
=> un+1 > un ∀n > 1 => dãy (un) là dãy số tăng.
* Lại có:
dãy (un) bị chặn dưới.
Câu 10: Xét tính tăng, giảm và bị chặn của dãy số (un) biết
A. Dãy số tăng, bị chặn trên B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn D. Cả A, B, C đều sai
Hiển thị đáp án
Đáp án: C
+ Với mọi n ∈ N* ta có : un > 0 . Xét tỉ số :
=> un+1 < un với mọi n.
=> Dãy số (un) là dãy số giảm.
+ Mặt khác : √(1 + n + n2) > 1 với ∀n ∈ N*
Vậy 0 < un < 1 nên dãy (un) là dãy bị chặn.
Câu 11: Xét tính tăng giảm và bị chặn của dãy số
A. Tăng, bị chặn B. Giảm, bị chặn
C. Tăng, chặn dưới D. Giảm, chặn trên
Hiển thị đáp án
Đáp án: B
*Trước hết bằng quy nạp ta chứng tỏ: 1 < un ≤ 2
Điều này đúng với n = 1.
Giả sử đúng với n = k + 1 tức là: 1 < uk ≤ 2. Ta chứng tỏ đúng với n = k+ 1.
Thật vậy ta có:
nên ta có đpcm.
Mà
Vậy dãy (un) là dãy giảm và bị chặn.
Câu 12: Xét tính tăng giảm và bị chặn của dãy số
A. Tăng, bị chặn B. Giảm, bị chặn
C. Tăng, chặn dưới D. Giảm, chặn trên
Hiển thị đáp án
Đáp án: A
*Trước hết ta chứng tỏ 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử đúng với n = k tức là: 1 < uk < 4. Ta chứng tỏ đúng với n = k + 1
Thật vậy: 1 < uk+1 = uk + √(uk-1) < √4 + √4 = 4
Vậy dãy (un) là bị chặn.
*Ta chứng tỏ (un) là dãy tăng
Ta có: u1 < u2, giả sử un+1 < un, ∀n ≥ k.
Khi đó:
=> dãy (un) là dãy tăng.
Vậy dãy (un) là dãy tăng và bị chặn.
Xem thêm những dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí!
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Nhóm học tập facebook miễn phí cho teen 2k5: fb.com/groups/hoctap2k5/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù phù hợp với nội quy phản hồi trang web sẽ bị cấm phản hồi vĩnh viễn.
day-so-cap-so-cong-va-cap-so-nhan.jsp
