Thủ Thuật về Viết phương trình tiếp tuyến của đường tròn tại điểm M 2022
Bùi Công Khanh đang tìm kiếm từ khóa Viết phương trình tiếp tuyến của đường tròn tại điểm M được Update vào lúc : 2022-08-06 22:36:03 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Phương trình tiếp tuyến của đường tròn tại 1 điểm, đi qua một điểm là dạng toán cơ bản cũng như thường gặp trong nội dung bài học kinh nghiệm tay nghề viết phương trình tiếp tuyến ?
Nội dung chính- Phương trình tiếp tuyến của đường tròn tại 1 điểm Phương trình tiếp tuyến của đường tròn đi qua 1 điểm Bài tập viết phương trình tiếp tuyến của đường tròn đi qua 1 điểm, tại 1 điểmVideo liên quan
Hãy cùng theo dõi ngay nội dung bài viết này để làm rõ hơn về nó thông qua công thức và bài tập minh họa rõ ràng nhất nhé !
Tham khảo nội dung bài viết khác:
Phương trình tiếp tuyến của đường tròn tại 1 điểm
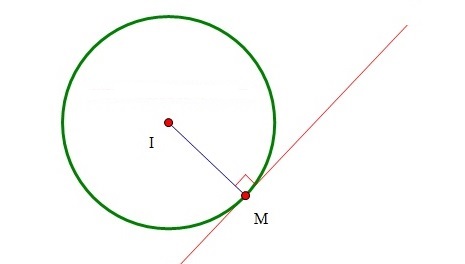
– Lập phương trình tiếp tuyến (d) của ( C ) tại điểm M:
+) Cho đường tròn ( C) có tâm I( a; b); bán kính R và điểm M( x0; y0) :
+) Do (d) là tiếp tuyến của đường tròn tại M nên d vuông góc IM

⇒ Phương trình đường thẳng d.
Phương trình tiếp tuyến của đường tròn đi qua 1 điểm
– Lập phương trình tiếp tuyến (d) của ( C) đi qua M:

⇒ (d): A(x – x0) + B( y – y0) = 0.
– Do đường thẳng d là tiếp tuyến của đường tròn ( C) nên d( I; d) = R
⇒ Một phương trình hai ẩn A; B. Giải phương trình ta được A = kB.
– Chọn A= … ⇒ B=…⇒ Phương trình đường thẳng d.
Bài tập viết phương trình tiếp tuyến của đường tròn đi qua 1 điểm, tại 1 điểm
Bài tập 1: Phương trình tiếp tuyến d của đường tròn (C): (x + 2)2 + (y + 2)2 = 25 tại điểm M(2; 1) là:
- A. d: -y + 1 = 0
B. d: 4x + 3y + 14 = 0
C. d: 3x – 4y – 2 = 0
D. d: 4x + 3y – 11 = 0
– Hướng dẫn giải
+ Đường tròn ( C) có tâm I(-2; -2) và bán kính R= 5.
+ Do đường thẳng d tiếp xúc với đường tròn taị điểm M nên hai tuyến đường thẳng d và IM vuông góc với nhau.

⇒Phương trình (d) : 4( x – 2) + 3( y – 1) = 0 hay 4x + 3y – 11 = 0
==> Đáp án D
Bài tập 2: Viết phương trình tiếp tuyến ∆ của đường tròn ( C): (x – 1)2 + (y + 2)2 = 8, biết tiếp tuyến đi qua điểm A( 5; -2).
- A. x – 5 = 0 .
B. x + y – 3 = 0 hoặc x – y 7 = 0.
C. x- 5= 0 hoặc x + y – 3 = 0 .
D. y + 2 = 0 hoặc x – y – 7 = 0 .
– Hướng dẫn giải

+ Nếu a = b; ta chọn a = 1 ⇒ b = 1. Khi đó phương trình tiếp tuyến ∆: x + y – 3 = 0
+ Nếu a = – b; chọn a = 1 thì b = – 1. Khi đó phương trình tiếp tuyến ∆: x – y – 7 = 0.
Vậy có hai tiếp tuyến thỏa mãn là x + y – 3 = 0 và x – y – 7 = 0
==> Đáp án B
Cám ơn bạn đã theo dõi những chia sẻ của Đồng Hành Cho Cuộc Sống Tốt Đẹp, hẹn hội ngộ bạn ở những nội dung bài viết chia sẻ nội dung tiếp theo của chúng tôi !
Dạng toán viết phương trình của đường tròn trong toán hình học lớp 10 sẽ là dạng toán xuất hiện trong đề thi trung học phổ thông quốc gia. Các em nên chú trọng vào phần này để nắm thật chắc kiến thức và kỹ năng, làm nền tảng để sẵn sàng sẵn sàng cho những kì thi nhé. Đồng thời, nội dung bài viết này sẽ đáp ứng những kiến thức và kỹ năng trọng tâm giúp những em ôn lại kiến thức và kỹ năng về phương trình đường tròn nhanh nhất có thể.
 Viết phương trình đường tròn
Viết phương trình đường trònPhương trình đường tròn có tâm I (a; b), bán kính R là:
(x – a)2 + (b – y)2 = R2
Phương trình đường tròn (x – a)2 + (b – y)2 = R2 hoàn toàn có thể viết dưới dạng:
x2 + y2 – 2ax – 2by + c = 0
Trong số đó: c = a2 + b2 – R2
trái lại, phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi a2 + b2 – c > 0.
Khi đó đường tròn (C) có tâm I (a; b) và bán kính R = √(a2 + b2 – c)
Cho điểm M0 (x0; y0) nằm trên đường tròn (C), tâm I (a; b). Gọi Δ là tiếp tiếp của (C) tại M0.
Ta có:
M0 thuộc Δ và vectơ IM0 = (x0 – a; y0 – b) là vectơ pháp tuyến của Δ.
Do đó phương trình của Δ là:
(x0 – a)(x – x0) + (y0 – b) (y – y0) = 0 (1)
Vậy phương trình (1) là phương trình tiếp tuyến của đường tròn (x – a)2 + (b – y)2 = R2 tại điểm M0 (x0; y0) nằm trên đường tròn.
 Phương trình tiếp tuyến đường tròn (C)
Phương trình tiếp tuyến đường tròn (C) 5 dạng toán phương trình đường tròn hay gặp
5 dạng toán phương trình đường tròn hay gặpÁp dụng kiến thức và kỹ năng:
– Phương trình đường tròn (C) có dạng: (x – a)2 + (b – y)2 = R2 thì có tâm I (a; b) và bán kính R.
– Phương trình có dạng x2 + y2 – 2ax – 2by + c = 0 và a2 + b2 – c > 0 thì phương trình đường tròn có tâm I (a; b) và bán kính R = √( a2 + b2 – c).
Phương pháp:
– Biến đổi phương trình về một trong hai dạng trên sau đó xác định tâm I và bán kính R.
Ví dụ: Tìm tâm và bán kính của đường tròn 2x2 + 2y2 – 8x – 4y – 6 = 0.
Ta có: 2x2 + 2y2 – 8x – 4y – 6 = 0
<=> x2 + y2 – 4x – 2y – 3 = 0
Ta có: a2 + b2 – c = 22 + 12 + 3 = 8 > 0 => Đây là phương trình đường tròn .
Phương trình đường tròn có tâm I (2; 1) và bán kinh R = √(a2 + b2 – c)= 2√2.
Phương pháp:
Cách 1:
– Tìm tọa độ tâm I (a; b) của đường tròn (C)
– Tìm bán kính R của (C)
– Viết phương trình đường tròn (C) dạng : (x – a)2 + (b – y)2 = R2
Cách 2:
– Giả sử phương trình đường tròn (C) có dạng: x2 + y2 – 2ax – 2by + c = 0
– Từ điều kiện bài toán đi qua những điểm (thường là 3 điểm ) rồi lập hệ phương trình 3 ẩn a, b, c.
– Giải hệ phương trình tìm được a, b, c rồi thay vào phương trình đường tròn (C).
– Kết luận phương trình đường tròn tìm được.
Ví dụ: Lập phương trình đường tròn (C) trong những trường hợp sau:
a) có tâm I (1; 3) và đi qua điểm O (0; 0)
b) Có đường kính AB với A (1; 1), B (5; 3)
c) Đi qua 3 điểm A (-1; 3), B (3; 5), C (4; -2).
Giải:
a) (C) có tâm I (1; 3) và đi qua điểm O (0; 0):
Ta có R = OI mà 
=> Đường tròn (C) có I (1; 3) và đi qua điểm O (0; 0) và bán kính R = √10
có phương trình:
(x – 1)2 + (y – 3)2 = 10.
b) (C) đường kính AB với A (1; 1), B (5; 3):
– Ta có tọa độ tâm I của (C0 là trung điểm của A, B là:
 và
và 
Bán kính là: 
=> Đường tròn (C) có I (3; 2) và bán kính R = √5 có phương trình là:
(x – 3)2 + (y – 2)2 = 5.
c) Đường tròn (C) đi qua 3 điểm A (-1; 3), B (3; 5), C (4; -2).
– Giả sử đường tròn (C) có dạng: x2 + y2 – 2ax – 2by + c = 0
– Vì (C) đi qua 3 điểm A (-1; 3), B (3; 5), C (4; -2) nên ta lần lượt thay tọa độ A, B, C vào (C), đã có được hệ phương trình sau:



– Giải hệ phương trình ta được: 
=> Phương trình đường tròn (C) là: 
Phương pháp:
– Dựa vào tính chất tiếp tuyến của đường tròn.
+ Đường tròn (C) tiếp xúc với đường thẳng (Δ) thì d[I, Δ ] = R
+ Đường tròn (C) tiếp xúc với đường thẳng (Δ) tại điểm A thì d[I, Δ ] = IA = R
+ Đường tròn (C) tiếp xúc với 2 đường thẳng (Δ1) và (Δ2) thì d[I, Δ1 ] = d[I, Δ2 ] R
Ví dụ: Lập phương trình đường tròn (C) trong mỗi trường hợp sau:
a) (C) có tâm I (2; 5) và tiếp xúc với Ox
b) (C) có tâm I (-1; 2) và tiếp xúc đường thẳng (Δ): x + 2y – 8 = 0
c) (C) đi qua A (2; -1) và tiếp xúc với 2 trục tọa độ Ox, Oy.
Giải:
a) (C) có tâm I (2; 5) và tiếp xúc với Ox:
– Ox có phương trình y = 0
– Bán kính R của đường tròn là khoảng chừng cách từ I đến Ox, ta có:
=> Phương trình đường tròn (C) có dạng: 
b) (C) có tâm I (-1; 2) và tiếp xúc đường thẳng (Δ): x + 2y – 8 = 0:
– Ta có: 

=> Phương trình đường tròn (C) có dạng: (x + 1)2 + (y – 5)2 = 5
c) (C) đi qua A (2; -1) và tiếp xúc với 2 trục tọa độ Ox, Oy:
– Vì A nằm ở góc phần tư thứ tư nên đường tròn cũng nằm trong góc phần tư thứ tư, nên tọa độ tâm I = (R; -R)
– Ta có: 
<=> R2 = R2 – 4R + 4 + R2 – 2R + 1
<=> R2 – 6R + 5 = 0
<=> R = 1 hoặc R = 5
=> Vậy có 2 đường tròn thỏa mãn điều kiện bài toán, đó là:
(C1): (x – 1)2 + (y – 1)2 = 1
(C2): (x – 5) 2 + (y + 5)2 = 25
Phương pháp:
Cách 1:
– Tính diện tích s quy hoạnh và nửa chu vi tam giác để tính được bán kính đường tròn r.
– Gọi I (a; b) là tâm đường tròn nội tiếp tam giác thì khoảng chừng cách từ tâm I tới 3 cạnh của tam giác là là bằng nhau và bằng r.
– Lập hệ phương trình 2 ẩn a, b
– Giải hệ phương trình 2 ẩn a, b và tìm được giá trị a, b.
Cách 2:
– Viết phương trình đường thẳng phân giác trong của 2 góc trong tam giác
– tìm giao điểm 2 đường phân giác đó ta được tâm I của đường tròn.
– Tính khoảng chừng cách từ I với 1 cạnh bất kì của tam giác ta tìm được bán kính.
ví dụ: Cho hai điểm A( 4; 0) và B (0; 3)
a) Viết phương trình đường tròn ngoại tiếp tam giác OAB
b) Viết phương trình đường tròn nội tiếp tam giác OAB
Giải:
a) Tam giác OAB vuông tại O nên tâm đường tròn ngoại tiếp tam giác OAB là trung điểm của cạnh AB, nên tâm I có tọa độ là I (2; 3/2)
=> Bán kính: R = IA = 5/2
=> Phương trình đường tròn ngoại tiếp tam giác OAB là: 
b)
– Ta có: 
– 
– 
– Vì đường tròn tiếp xúc với 2 trục tọa độ nên tâm Ir = (r; r) = (1; 1)
=> Phương trình đường tròn là : (x – 1)2 + (y – 1)2 = 1.
Phương pháp:
– Viết phương trình đường trung trực d của đoạn AB.
– Xác định tâm I là giao điểm của d
– Bán kính R = IA
Ví dụ: Viết phương trình đường tròn T đi qua 2 điểm A(5:-1) B(-2;-2). Tâm I thuộc đường thẳng d: 3x-2y+1=0
Giải:

 Đề số 1
Đề số 1 Đề số 2
Đề số 2 Đề số 3
Đề số 3Những bài tập mà lessonopoly chia sẻ trên đây sẽ giúp những em vận dụng được kiến thức và kỹ năng lý thuyết đã học. Hy vọng những em hoàn toàn có thể làm tốt những bài tập trên. Cùng chia sẻ tài liệu có ích và những bài tập hay về phương trình đường tròn này cho những bạn cùng làm nhé.
