Thủ Thuật về Hàm số f(x) xác định trên D là hàm số chẵn khi 2022
Hà Trần Thảo Minh đang tìm kiếm từ khóa Hàm số f(x) xác định trên D là hàm số chẵn khi được Update vào lúc : 2022-11-07 02:50:11 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.Phương pháp chứng tỏ tính chẵn , lẻ của hàm số
–o0o—
Định nghĩa :
Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu :
x ∈ D thì -x ∈ D và f(-x) = f(x).
lưu ý : đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu :
x ∈ D thì -x ∈ D và f(-x) = -f(x).
lưu ý : đồ thị của hàm số lẻ nhận góc tọa độ làm tâm đối xứng.
+ D là tập đối xứng có dạng : [-a; a] với a ∈ R.
————————–
Phương pháp :
Bước 1 : tìm TXĐ : D chứng tỏ D là tập đối xứng.
Bước 2 : lấy x ∈ D => – x ∈ D.
Bước 3 : xét : f(-x) :
- Nếu f(-x) = … = f(x) : hàm số chẵn.Nếu f(-x) = …
= – f(x) : hàm số lẻ.Nếu f(-x) = … ≠ – f(x) hoặc f(x): hàm số không chẵn, lẻ.
—————————-
Bài tập 1 : Xét tính chẵn lẻ của hàm số : y = f(x) = x3 + x
TXĐ : D = R
=> D là tập đối xứng.
lấy x ∈ D => – x ∈ D.
Xét f(-x) = (-x)3 + (-x) = -( x3 + x)= -f(x)
=> f(-x) = – f(x)
vậy : hàm số y = x3 + x là hàm số lẻ.
Bài tập 2: Xét tính chẵn lẻ của hàm số : y = f(x) = x4 + x2 – 2
TXĐ : D = R
=> D là tập đối xứng.
lấy x ∈ D => – x ∈ D.
Xét : f(-x) = (-x)4 + (-x)2 – 2 = x4 + x2 – 2 = f(x)
=> f(-x) = f(x)
Vậy : hàm số y = x4 + x2 – 2 là hàm số chẵn.
Bài tập 3 : Xét tính chẵn lẻ của hàm số : y = f(x) = – 5
TXĐ : 2x + 8 ≥ 0 <=> x ≥ – 4
D = [-4; + ∞)
ta có : 5 ∈ D mà – 5 ∉ D => D không là tập đối xứng.
vậy : hàm số không chẵn, không lẻ.
Bài tập 4: Xét tính chẵn lẻ của hàm số : y = f(x) =
Đk :$latex begincases
x+3 geq 0\
3-x geq 0
endcases
Leftrightarrow begincases
x geq -3\
x leq 3
endcases
Leftrightarrow -3 leq x leq 3$
Vậy : D = [-3; 3] : miền đối xứng.
lấy x ∈ D => – x ∈ D.
Xét : f(-x) = = f(x)
=> f(-x) = f(x)
=> hàm số y = là hàm số chẵn.
[embed]https://www.youtube.com/watch?v=hkB3d-IEI58[/embed]
Bài tập rèn luyện : Xét tính chẵn – lẻ của những hàm số sau :

Để xác định tính chẵn lẻ của hàm số trước tiên tất cả chúng ta cần hiểu thế nào là hàm số chẵn và thế nào là hàm số lẻ.
Bài viết này tất cả chúng ta cùng tìm hiểu cách xác định hàm số chẵn lẻ, đặc biệt là cách xét tính chẵn lẻ của hàm số có trị tuyệt đối. Qua đó vận dụng giải một số trong những bài tập để rèn kỹ năng giải toán này.
» Đừng bỏ lỡ: Tổng hợp những dạng toán về hàm số số 1 và hàm số bậc 2 cực hay
1. Kiến thức cần nhớ hàm số chẵn, hàm số lẻ
• Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu: ∀x ∈ D thì -x ∈ D và f(-x) = f(x).
* Ví dụ: Hàm số y = x2 là hàm số chẵn
- Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
• Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu: ∀x ∈ D thì -x ∈ D và f(-x) = -f(x).
* Ví dụ: Hàm số y = x là hàm số lẻ
- Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
• Chú ý: Một hàm số không nhât thiết phải là hàm số chẵn hoặc hàm số lẻ.
* Ví dụ: Hàm số y = 2x + 1 không là hàm số chẵn, cũng không là hàm số lẻ vì:
Tại x = 1 có f(1) = 2.1 + 1 = 3
Tại x = -1 có f(-1) = 2.(-1) + 1 = -1
→ Hai giá trị f(1) và f(-1) không bằng nhau và cũng không đối nhau
2. Cách xét tính chẵn lẻ của hàm số, hàm số có trị tuyệt đối
* Để xác định hàm số chẵn lẻ ta thực hiện tiến trình sau:
- Bước 1: Tìm TXĐ: D
Nếu ∀x ∈ D ⇒ -x ∈ D Chuyển qua bước ba
Nếu ∃ x0 ∈ D ⇒ -x0 ∉ D kết luận hàm không chẵn cũng không lẻ.
- Bước 2: Thay x bằng -x và tính f(-x)
- Bước 3: Xét dấu (so sánh f(x) và f(-x)):
° Nếu f(-x) = f(x) thì hàm số f chẵn
° Nếu f(-x) = -f(x) thì hàm số f lẻ
° Trường hợp khác: hàm số f không còn tính chẵn lẻ

3. Một số bài tập xét tính chẵn lẻ của hàm số
* Bài tập 1 (Bài 4 trang 39 SGK Đại số 10): Xét tính chẵn lẻ của những hàm số sau:
a) y = |x|;
b) y = (x + 2)2;
c) y = x3 + x;
d) y = x2 + x + 1.
° Lời giải bài tập 1 (bài 4 trang 39 SGK Đại số 10):
a) Đặt y = f(x) = |x|.
° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
° f(–x) = |–x| = |x| = f(x).
→ Vậy hàm số y = |x| là hàm số chẵn.
b) Đặt y = f(x) = (x + 2)2.
° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
° f(–x) = (–x + 2)2 = (x – 2)2 ≠ (x + 2)2 = f(x)
° f(–x) = (–x + 2)2 = (x – 2)2 ≠ – (x + 2)2 = –f(x).
→ Vậy hàm số y = (x + 2)2 làm hàm số không chẵn, không lẻ.
c) Đặt y = f(x) = x3 + x.
° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
° f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
→ Vậy y = x3 + x là hàm số lẻ.
d) Đặt y = f(x) = x2 + x + 1.
° TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
° f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ x2 + x + 1 = f(x)
° f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ –(x2 + x + 1) = –f(x)
→ Vậy hàm số y = x2 + x + 1 là hàm số không chẵn, không lẻ.


* Bài 3:Xét tính chẵn lẻ của hàm số có trị tuyệt đối sau: f(x) = |x + 3| - |x - 3|
° Lời giải:
Với f(x) = |x + 3| - |x - 3|
- TXĐ: D = R
f(-x) = |-x + 3| - |-x - 3| = |-(x - 3)| - |-(x + 3)| = |x - 3| - |x + 3| = -f(x).
→ Kết luận: hàm f(x) = |x + 3| - |x - 3| là hàm số lẻ.


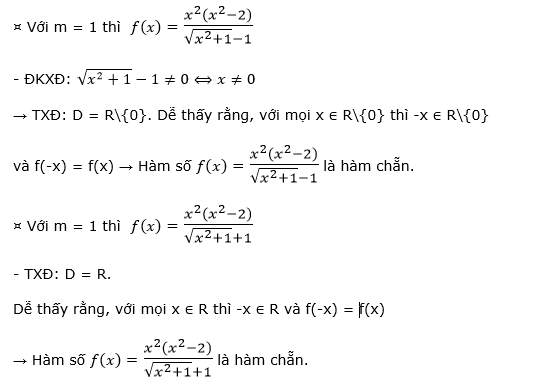
⇒ Vậy với m = ± 1 thì hàm số đã cho là hàm chẵn.
4. Bài tập xét tính chẵn lẻ của hàm số
* Bài 1: Khảo sát tính chẵn lẻ của những hàm số có trị tuyệt đối sau
a) f(x) = |2x + 1| + |2x - 1|
b) f(x) = (|x + 1| + |x - 1|)/(|x + 1| - |x - 1|)
a) f(x) = |x - 1|2.
° Đ/s: a) chẵn; b) lẻ; c) không chẵn, không lẻ.
* Bài 2: Cho hàm số f(x) = (m - 2)x2 + (m - 3)x + mét vuông - 4
a) Tìm m để hàm f(x) là hàm chẵn
b) Tìm m để hàm f(x) là hàm lẻ.
° Đ/s: a) m = 3; b) m = 2.
Như vậy, ở phần nội dung này những em cần nhớ được định nghĩa hàm số chẵn, hàm số lẻ, 3 bước cơ bản để xét tính chẵn lẻ của hàm số, hàm có trị tuyệt đối, hàm chứa căn thức và những hàm khác. Đặc biệt cần luyện qua nhiều bài tập để rèn luyện kỹ năng giải toán của tớ mình.
Hy vọng với nội dung bài viết về cách xét tính chẵn lẻ của hàm số, hàm có trị tuyệt đối và bài tập của Hay Học Hỏi ở trên giúp ích cho những em. Mọi góp ý và thắc mắc những em hãy để lại nhận xét dưới nội dung bài viết để ghi nhận và tương hỗ, chúc những em học tốt.
Tải thêm tài liệu liên quan đến nội dung bài viết Hàm số f(x) xác định trên D là hàm số chẵn khi